湘教版必修11.1集合导学案及答案
展开集合的概念(预习学案)
一、预习目标:
(1)使学生初步理解集合的概念,知道常用数集的概念及其记法
(2)使学生初步了解“属于”关系的意义
(3)使学生初步了解有限集、无限集的意义
二、预习方法:
独立思考,生生交流,小组交流,师生交流。
三、预习提纲:
1、阅读教材第一部分,问题如下:
(1)有那些概念?是如何定义的?
(2)有那些符号?是如何表示的?
(3)集合中元素的特性是什么?要正确认识集合中元素的特性
学生可以独立思考,可以讨论交流,教师巡视指导。
2、阅读教材第二部分,问题如下:
(1).集合的表示方法有几种?分别是如何定义的?
(2).有限集、无限集、空集的概念是什么?试各举一例。
四、典型习题:
1、教材练习
2、下列各组对象能确定一个集合吗?
(1)所有很大的实数。 ( )
(2)好心的人。 ( )
(3)1,2,2,3,4,5.( )
五、预见性问题:
1、在预习集合中元素的特性时,可能有部分同学忽略,
(1)、确定性:
按照明确的判断标准给定一个元素或者在这个集合里,或者不在,不能模棱两可。集合中的元素必须是确定的.这就是说,给定一个集合,任何一个对象是不是这个集合的元素也就确定了.例如,给出集合{地球上的四大洋},它的元素是:太平洋、大西洋、印度洋、北冰洋.其他对象都不用于这个集合.如果说“由接近 的数组成的集合”,这里“接近 的数”是没有严格标准、比较模糊的概念,它不能构成集合.
(2)、互异性:
集合中的元素是互异的.这就是说,集合中的元素是不能重复的,集合中相同的元素只能算是一个.例如方程x2+2x+1=0有两个重根,其解集只能记为{1},而不能记为{1,1}.
(3)、无序性:
集合中的元素没有一定的顺序(通常用正常的顺序写出).集合中的元素是不分顺序的.集合和点的坐标是不同的概念,在平面直角坐标系中,点(l,0)和点(0,l)表示不同的两个点,而集合{1,0}和{0,1}表示同一个集合.
2、注意:
(1)、集合通常用大写的拉丁字母表示,如A、B、C、P、Q……
元素通常用小写的拉丁字母表示,如a、b、c、p、q……
(2)、“∈”的开口方向,不能把a∈A颠倒过来写。
(3)、集合和元素是两个不同的概念,符号∈是表示元素和集合之间关系的,不能用来表示集合之间的关系
(4)、集合具有两方面的意义,即:凡是符合条件的对象都是它的元素;只要是它的元素就必须符合条件.
(5)、一些对象一旦组成了集合,那么这个集合的元素就是这些对象的全体,而非个别现象.
六、预习疑难反馈:
在预习课的最后,以小组为单位,讨论交流,组长提本组在预习过程中遇到的疑难点,教师搜集整理,为展示课作好充分的准备。
七、思考并回答以下问题:
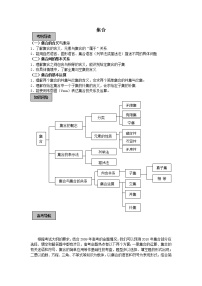
(1) 试画出集合一节的知识结构图
(2) 什么叫交集、并集、补集?符号语言如何表示?图形语言?
(3) 交、并、补有何综合性质?
八、例题思考:
例1:设U=R,A={x|-5<x<5},B={x|0≦x<7},求A∩B、A∪B、CA 、CB、(CA)∩(CB)、(CA)∪(CB)、C(A∪B)、C(A∩B)。
例2:全集U={x|x<10,x∈N},AU,BU,(CB)∩A={1,9},A∩B={3},CA)∩(CB)={4,6,7},求A、B。
湘教版必修11.1集合学案: 这是一份湘教版必修11.1集合学案,共6页。
高中数学湘教版必修11.1集合导学案: 这是一份高中数学湘教版必修11.1集合导学案,共14页。
湘教版必修11.1集合导学案: 这是一份湘教版必修11.1集合导学案,共39页。