湘教版必修11.1集合导学案

集合与简易逻辑  知识要点

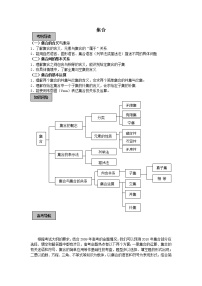
一、知识结构:

本章知识主要分为集合、简单不等式的解法（集合化简）、简易逻辑三部分：

二、知识回顾：

2. 集合

4. 基本概念：集合、元素；有限集、无限集；空集、全集；符号的使用.
5. 集合的表示法：列举法、描述法、图形表示法.

集合元素的特征：确定性、互异性、无序性.

集合的性质：

①任何一个集合是它本身的子集，记为；

②空集是任何集合的子集，记为；

③空集是任何非空集合的真子集；

如果，同时，那么A = B.

如果.

[注]：①Z= {整数}（√）   Z ={全体整数} （×）

②已知集合S 中A的补集是一个有限集，则集合A也是有限集.（×）（例：S=N； A=，则CsA= {0}）

③ 空集的补集是全集.          

④若集合A=集合B，则CBA = ， CAB  =     CS（CAB）= D     （ 注 ：CAB  = ）.

3. ①{（x，y）|xy =0，x∈R，y∈R}坐标轴上的点集.

②{（x，y）|xy＜0，x∈R，y∈R二、四象限的点集.   

③{（x，y）|xy＞0，x∈R，y∈R} 一、三象限的点集.

[注]：①对方程组解的集合应是点集.

例：   解的集合{(2，1)}.

②点集与数集的交集是. （例：A ={(x，y)| y =x+1}  B={y|y =x2+1}  则A∩B =）

4. ①n个元素的子集有2n个.  ②n个元素的真子集有2n －1个.   ③n个元素的非空真子集有2n－2个.

5. ⑴①一个命题的否命题为真，它的逆命题一定为真. 否命题逆命题.

②一个命题为真，则它的逆否命题一定为真. 原命题逆否命题.

例：①若应是真命题.

解：逆否：a = 2且 b = 3，则a+b = 5，成立，所以此命题为真.

②     .

解：逆否：x + y =3x = 1或y = 2.

,故是的既不是充分，又不是必要条件.

⑵小范围推出大范围；大范围推不出小范围.

6. 例：若.  
7. 集合运算：交、并、补.

8. 主要性质和运算律

1. 包含关系：
2. 等价关系：
3. 集合的运算律：

交换律：      

结合律:      

分配律:.

0-1律：

等幂律：

求补律：A∩CUA=φ  A∪CUA=U CUU=φ CUφ=U

反演律：CU(A∩B)= (CUA)∪(CUB)   CU(A∪B)= (CUA)∩(CUB)

9. 有限集的元素个数

定义：有限集A的元素的个数叫做集合A的基数，记为card( A)规定 card(φ) =0.

基本公式：

(3) card(UA)= card(U)- card(A)

 (二)含绝对值不等式、一元二次不等式的解法及延伸

  1.整式不等式的解法

根轴法（零点分段法）

①将不等式化为a0(x-x1)(x-x2)…(x-xm)>0(<0)形式，并将各因式x的系数化“+”；(为了统一方便)

②求根，并在数轴上表示出来；

③由右上方穿线，经过数轴上表示各根的点（为什么？）；

④若不等式（x的系数化“+”后）是“>0”,则找“线”在x轴上方的区间；若不等式是“<0”,则找“线”在x轴下方的区间.

     （自右向左正负相间）

则不等式的解可以根据各区间的符号确定.

特例① 一元一次不等式ax>b解的讨论；

②一元二次不等式ax2+box>0(a>0)解的讨论.

2.分式不等式的解法

（1）标准化：移项通分化为>0(或<0)； ≥0(或≤0)的形式，

（2）转化为整式不等式（组）

3.含绝对值不等式的解法

（1）公式法：,与型的不等式的解法.

（2）定义法：用“零点分区间法”分类讨论.

（3）几何法：根据绝对值的几何意义用数形结合思想方法解题.

4.一元二次方程根的分布

一元二次方程ax2+bx+c=0(a≠0)

（1）根的“零分布”：根据判别式和韦达定理分析列式解之.

（2）根的“非零分布”：作二次函数图象，用数形结合思想分析列式解之.

（三）简易逻辑

1、命题的定义：可以判断真假的语句叫做命题。

2、逻辑联结词、简单命题与复合命题：

“或”、“且”、“非”这些词叫做逻辑联结词；不含有逻辑联结词的命题是简单命题；由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题。

构成复合命题的形式：p或q(记作“p∨q” )；p且q(记作“p∧q” )；非p(记作“┑q” ) 。

3、“或”、  “且”、  “非”的真值判断

（1）“非p”形式复合命题的真假与F的真假相反；

（2）“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；

（3）“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．

4、四种命题的形式：

原命题：若P则q；  逆命题：若q则p；

否命题：若┑P则┑q；逆否命题：若┑q则┑p。

(1)交换原命题的条件和结论，所得的命题是逆命题；

 (2)同时否定原命题的条件和结论，所得的命题是否命题；

 (3)交换原命题的条件和结论，并且同时否定，所得的命题是逆否命题．

5、四种命题之间的相互关系：

一个命题的真假与其他三个命题的真假有如下三条关系：(原命题逆否命题)

①、原命题为真，它的逆命题不一定为真。

②、原命题为真，它的否命题不一定为真。

③、原命题为真，它的逆否命题一定为真。

6、如果已知pq那么我们说，p是q的充分条件，q是p的必要条件。

若pq且qp,则称p是q的充要条件，记为p⇔q.

7、反证法：从命题结论的反面出发（假设），引出(与已知、公理、定理…)矛盾，从而否定假设证明原命题成立，这样的证明方法叫做反证法。