湘教版1.1集合导学案及答案

集合

（一）集合的含义与表示

1．了解集合的含义、元素与集合的“属于”关系.

2．能用自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题

（二）集合间的基本关系

1．理解集合之间包含与相等的含义，能识别给定集合的子集.

2．在具体情境中，了解全集与空集的含义.

（三）集合的基本运算

1．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集。

2．理解在给定集合中一个子集的补集的含义，会求给定子集的补集.

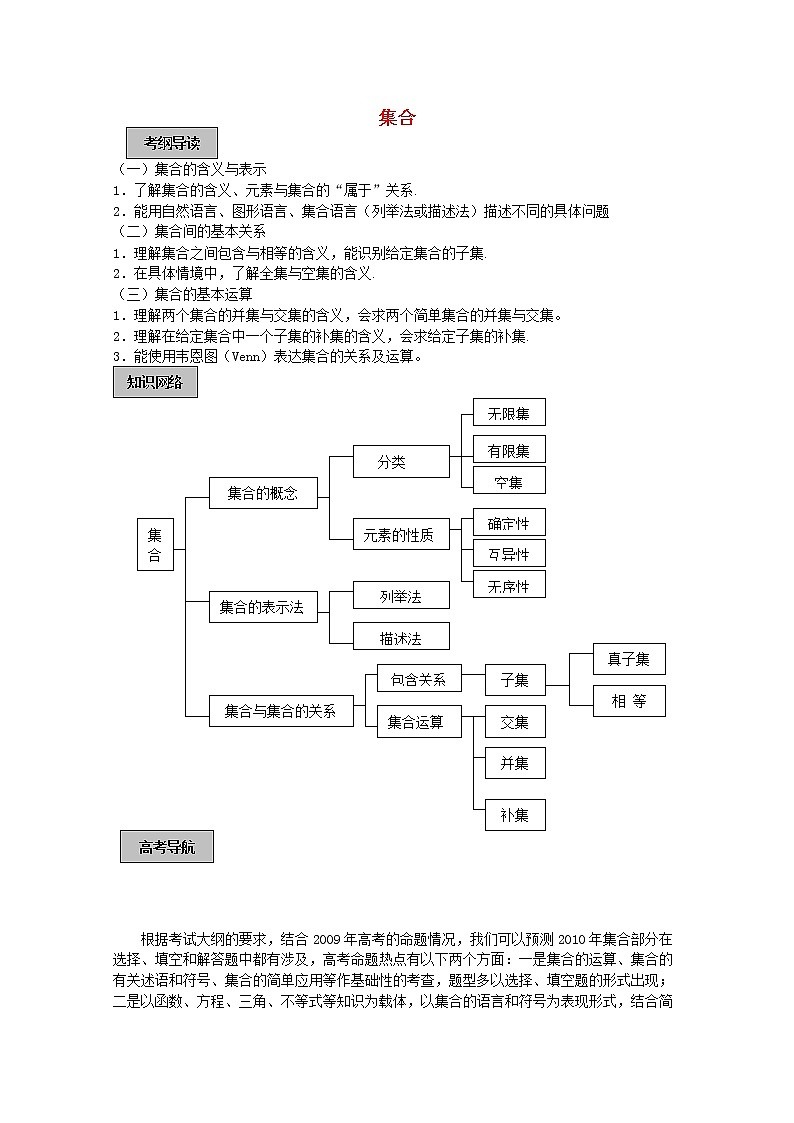
3．能使用韦恩图（Venn）表达集合的关系及运算。

根据考试大纲的要求，结合2009年高考的命题情况，我们可以预测2010年集合部分在选择、填空和解答题中都有涉及，高考命题热点有以下两个方面：一是集合的运算、集合的有关述语和符号、集合的简单应用等作基础性的考查，题型多以选择、填空题的形式出现；二是以函数、方程、三角、不等式等知识为载体，以集合的语言和符号为表现形式，结合简易逻辑知识考查学生的数学思想、数学方法和数学能力，题型常以解答题的形式出现

第1课时    集合的概念

一、集合

1．集合是一个不能定义的原始概念，描述性定义为：某些指定的对象        就成为一个集合，简称       ．集合中的每一个对象叫做这个集合的         

2．集合中的元素属性具有：

(1) 确定性；  (2)          ； (3)           ．

3．集合的表示法常用的有           、           和韦恩图法三种，有限集常用           ，无限集常用           ，图示法常用于表示集合之间的相互关系．

二、元素与集合的关系

4．元素与集合是属于和           的从属关系，若a是集合A的元素，记作          ，若a不是集合B的元素，记作           ．但是要注意元素与集合是相对而言的．

三、集合与集合的关系

5．集合与集合的关系用符号           表示．

6．子集：若集合A中           都是集合B的元素，就说集合A包含于集合B（或集合B包含集合A），记作          

7．相等：若集合A中           都是集合B的元素，同时集合B中           都是集合A的元素，就说集合A等于集合B，记作           ．

8．真子集：如果           就说集合A是集合B的真子集，记作           ．

9．若集合A含有n个元素，则A的子集有           个，真子集有           个，非空真子集有           个．

10．空集是一个特殊而又重要的集合，它不含任何元素，是任何集合的           ，是任何非空集合的           ，解题时不可忽视．

例1. 已知集合，试求集合的所有子集.

解：由题意可知是的正约数，所以 可以是；相应的为

，即.

 ∴的所有子集为.

变式训练1.若a,bR,集合求b-a的值.

解：由可知a≠0，则只能a+b=0，则有以下对应关系：

  ①或      ②

由①得符合题意；②无解.所以b-a=2.

例2. 设集合，，，求实数a的值.

解：此时只可能，易得或。

当时，符合题意。

当时，不符合题意，舍去。

故。

变式训练2：（1）P＝{x|x2－2x－3＝0}，S＝{x|ax＋2＝0}，SP，求a取值？

（2）A＝{－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，BA,求m。

解：（1）a＝0,S＝，P成立      a0，S，由SP，P＝{3，－1}

得3a＋2＝0，a＝－或－a＋2＝0，a＝2；    ∴a值为0或－或2.

（2）B＝，即m＋1>2m－1,m<2  ∴A成立.

      B≠，由题意得得2≤m≤3

∴m<2或2≤m≤3      即m≤3为取值范围.

注：（1）特殊集合作用，常易漏掉

例3. 已知集合A={x|mx2-2x+3=0，m∈R}.

（1）若A是空集，求m的取值范围；

（2）若A中只有一个元素，求m的值；

（3）若A中至多只有一个元素，求m的取值范围.

解： 集合A是方程mx2-2x+3=0在实数范围内的解集.

(1)∵A是空集，∴方程mx2-2x+3=0无解.

∴Δ=4-12m<0,即m>.

（2）∵A中只有一个元素，

∴方程mx2-2x+3=0只有一个解.

若m=0，方程为-2x+3=0，只有一解x=;

若m≠0，则Δ=0，即4-12m=0,m=.

∴m=0或m=.

(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义，根据（1）、（2）的结果，

得m=0或m≥.

变式训练3.（1）已知A={a+2，（a+1）2，a2+3a+3}且1∈A，求实数a的值；

（2）已知M={2，a，b}，N={2a，2，b2}且M=N，求a，b的值.

解：（1）由题意知：

a+2=1或(a+1)2=1或a2+3a+3=1，

∴a=-1或-2或0，根据元素的互异性排除-1，-2,∴a=0即为所求.

（2）由题意知,或或或

根据元素的互异性得或即为所求.

例4. 若集合A＝{2，4，}，B＝{1，a＋1，，、 }，且A∩B＝{2，5}，试求实数的值．

解:∵А∩В＝{2，5}，∴2∈A且5∈A，

则＝5(a－2)(a－1)(a＋1)＝0，

∴a＝－1或a＝1或a＝2．

当a＝－1时，B＝{1，0，5，2，4}，与A∩B＝{2，5}矛盾，∴a≠－1．

当a＝1时，B＝{1，2，1，5，12}，与集合中元素互异性矛盾，∴a≠1．

当a＝2时，B＝{1，3，2，5，25}，满足A∩B＝{2，5}．故所求a的值为2．

变式训练4.已知集合A＝{a，a＋d，a＋2d}，B＝{a，aq， }，其中a≠0，若A＝B，求q的值

解：∵A＝B

∴(Ⅰ)或 (Ⅱ)

由(Ⅰ)得q＝1，由(Ⅱ)得q＝1或q＝－．

当q＝1时，B中的元素与集合元素的互异性矛盾

∴q＝－

1．本节的重点是集合的基本概念和表示方法，对集合的认识，关键在于化简给定的集合，确定集合的元素，并真正认识集合中元素的属性，特别要注意代表元素的形式，不要将点集和数集混淆．

2．利用相等集合的定义解题时，特别要注意集合中元素的互异性，对计算的结果要加以检验．

3．注意空集φ的特殊性，在解题时，若未指明集合非空，则要考虑到集合为空集的可能性．

4．要注意数学思想方法在解题中的运用，如化归与转化、分类讨论、数形结合的思想方法在解题中的应用．

第2课时    集合的运算

一、集合的运算

1．交集：由           的元素组成的集合，叫做集合A与B的交集，记作A∩B，即A∩B＝            ．

2．并集：由            的元素组成的集合，叫做集合A与B的并集，记作A∪B，即A∪B＝           ．

3．补集：集合A是集合S的子集，由           的元素组成的集合，叫做S中子集A的补集，记作，即＝           ．

二、集合的常用运算性质

1．A∩A＝          ，A∩＝          ，A∩B=          ，B∩A，A∪A＝          ，

A∪＝           ，A∪B＝B∪A

2．＝          ，＝          ，           ．

3．          ，

          ，

4．A∪B＝A         

A∩B＝A         

例1. 设全集，方程有实数根，方程

有实数根，求.

解：当时，，即；

当时，即，且 ∴，

∴

而对于，即，∴.

∴

变式训练1.已知集合A=B= 

（1）当m=3时，求；

（2）若AB，求实数m的值.

解：  由得∴-1＜x≤5,∴A=.

（1）当m=3时，B=，则=，

∴=.

(2)∵A=∴有42-2×4-m=0,解得m=8.

此时B=,符合题意，故实数m的值为8.

例2. 已知,或.

(1)若,求的取值范围;

(2) 若,求的取值范围.

解:(1),  ∴，解之得.

(2) ,  ∴.  ∴或，  或

∴若,则的取值范围是；若,则的取值范围是.

变式训练2：设集合A=B

（1）若AB求实数a的值；

（2）若AB=A，求实数a的取值范围；

（3）若U=R，A（）=A.求实数a的取值范围.

解:由x2-3x+2=0得x=1或x=2,故集合A=  

（1）∵AB∴2B，代入B中的方程，

得a2+4a+3=0,∴a=-1或a=-3;

当a=-1时，B=满足条件；

当a=-3时，B=满足条件；

综上，a的值为-1或-3.   

（2）对于集合B，

=4（a+1）2-4(a2-5)=8(a+3).

∵AB=A，∴BA,

①当＜0,即a＜-3时，B=，满足条件；

②当=0，即a=-3时，B，满足条件；

③当＞0，即a＞-3时，B=A=才能满足条件，

则由根与系数的关系得

即矛盾；

综上，a的取值范围是a≤-3.

（3）∵A（）=A，∴A，∴A  

①若B=，则＜0适合；

②若B≠，则a=-3时，B=，AB=，不合题意；

a＞-3，此时需1B且2B，将2代入B的方程得a=-1或a=-3（舍去）；

将1代入B的方程得a2+2a-2=0

∴a≠-1且a≠-3且a≠-1 

综上，a的取值范围是a＜-3或-3＜a＜-1-或-1-＜a＜-1或-1＜a＜-1+或a＞-1+. 

例3. 已知集合A=B，试问是否存在实数a，使得AB  若存在，求出a的值；若不存在，请说明理由.

解:方法一  假设存在实数a满足条件AB=则有

（1）当A≠时，由AB=，B，知集合A中的元素为非正数，

设方程x2+(2+a)x+1=0的两根为x1,x2,则由根与系数的关系，得

（2）当A=时，则有=(2+a)2-4＜0，解得-4＜a＜0.

综上（1）、（2），知存在满足条件AB=的实数a,其取值范围是（-4，+∞）.

方法二  假设存在实数a满足条件AB≠，则方程x2+(2+a)x+1=0的两实数根x1，x2至少有一个为正，

因为x1·x2=1＞0，所以两根x1,x2均为正数.

则由根与系数的关系，得解得

又∵集合的补集为

∴存在满足条件AB=的实数a,其取值范围是（-4，+∞）.

变式训练3.设集合A={（x,y）|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*}，问是否存在非零整数a,使A∩B≠？若存在，请求出a的值；若不存在，说明理由.

解：假设A∩B≠，则方程组

有正整数解，消去y,得ax2-(a+2)x+a+1=0.

由Δ≥0，有（a+2）2-4a(a+1)≥0,解得-.因a为非零整数，∴a=±1，

当a=-1时，代入（*），解得x=0或x=-1,

而x∈N*.故a≠-1.当a=1时，代入（*）,

解得x=1或x=2，符合题意.故存在a=1,使得A∩B≠,

此时A∩B={（1，1），（2，3）}.

例4. 已知A＝{x｜x2－2ax＋(4a－3)＝0，x∈R}，又B＝{x｜x2－2ax＋a2＋a＋2＝0，x∈R}，是否存在实数a，使得AB＝?若存在，求出实数的值；若不存在，说明理由．

解：1<a<2即实数(1，2)时，＝．

变式训练4.设集合为函数的定义域,集合为函数的值域,集合为不等式的解集.（1）求；（2）若,求的取值范围．

解：（1）解得A=（-4，2）， B= 。  所以

（2）a的范围为<0  

1．在解决有关集合运算题目时，关键是准确理解题目中符号语言的含义，善于转化为文字语言．

2．集合的运算可以用韦恩图帮助思考，实数集合的交、并运算可在数轴上表示，注意在运算中运用数形结合思想．

3．对于给出集合是否为空集，集合中的元素个数是否确定，都是常见的讨论点，解题时要有分类讨论的意识.

集合测试题

一、选择题

1．设全集U=R，A={x∈N︱1≤x≤10}，B={ x∈R︱x 2+ x－6=0}，则下图中阴影表示的集合为（    ）

A．{2}        B．{3}       C．{－3，2}         D．{－2，3}

2．当xR，下列四个集合中是空集的是（    ）

A. {x|x2-3x+2=0}              B. {x|x2＜x}

C. {x|x2-2x+3=0}              C. {x|sinx+cosx=}

3．设集合，集合，若, 则等于（    ）

A.                           B.   

C.                           D.

4．设集合，，则下列关系中正确的是（  ）

A．       B．         C．            D．

5．设M，P是两个非空集合，定义M与P的差集为M-P={x|xM且xp},则M-（M-P）等于（    ）

A. P      B. MP     C. MP      D. M

6．已知, 若, 则实数的取值范围是(   )

A.          B.           C.           D.

7.集合M＝{x｜x＝sin，n∈Z}，N＝{ x｜x＝cos，n∈Z }，M∩N＝ （  ）

A．         B． 

C．{0}               D．

8.已知集合M＝{x｜}，N＝{x│}，则  （  ）

A．M＝N   B．M   N

C．M   N   D．MN＝φ

9． 设全集∪＝{x｜1≤x <9，x∈N}，则满足的所有集合B的个数有 （  ）

A．1个            B．4个      

C．5个            D．8个

10．已知集合M＝{(x，y)︱y＝}，N＝{(x，y)︱y＝x＋b}，且M∩N＝，则实数b应满足的条件是

（  ）

A．︱b︱≥              B．0＜b＜

C．－3≤b≤             D．b＞或b＜－3

二、填空题

11．设集合,,且，则实数的取值范围是                   .

12．设全集U=R，A=，

则右图中阴影部分表示的集合为                 .

13．已知集合A=，那么A的真子集的个数是               .

14．若集合，，则等于        .

15．满足的集合A的个数是_______个.

16．已知集合，函数的定义域为Q.

（1）若，则实数a的值为          ；

（2）若，则实数a的取值范围为            .

三、解答题

17．已知函数的定义域集合是A,函数的定义域集合是B

（1）求集合A、B

（2）若AB=B,求实数的取值范围．

18．设，集合，；

若，求的值. 

19．设集合，.  

(1)当时，求A的非空真子集的个数；

(2)若B=，求m的取值范围；

(3)若，求m的取值范围.

20. 对于函数f(x)，若f(x)＝x，则称x为f(x)的“不动点”，若，则称x为f(x)的“稳定点”，函数f(x)的“不动点”和“稳定点”的集合分别记为A和B，即}，.

(1)  求证：AB

(2) 若，且，求实数a的取值范围.

参考答案

一、选择题

1．答案：A

2．答案：C

3．答案：A

4．提示：，.答案： D

5．答案：B

6．答案：B

7. 由与的终边位置知M＝{，0，}，N＝{－1，0，1}，故选C.  

8.C

9.D

10.D

11．提示:,  ∴,答案：

12．答案：，图中阴影部分表示的集合为,

13．答案：15

14. 答案：

15. 答案：7

16. 答案：；

17. 解：（1）A＝…………

B＝……………

（2）由AB＝B得AB，因此……………

所以,所以实数ａ的取值范围是……………

18. 解：，由，

当时，，符合；

当时，，而，∴，即

∴或. 

19. 解：化简集合A=，集合B可写为

(1),即A中含有8个元素，A的非空真子集数为

（个）.

(1)显然只有当m-1=2m+1即m=--2时，B=.

(2)当B=即m=-2时，；

当B即时

（ⅰ）当m<-2 时，B=(2m-1,m+1),要

只要，所以m的值不存在；

（ⅱ）当m>-2 时,B=（m-1,2m+1）,要

只要.

综合，知m的取值范围是：m=-2或

20.证明(1).若A＝，则AB 显然成立；

若A≠，设t∈A，则f(t)＝t，f(f(t))＝f(t)＝t，即t∈B，从而 AB.

解 (2)：A中元素是方程f(x)＝x 即的实根.

     由 A≠，知 a＝0 或     

即 

B中元素是方程

即  的实根

由AB，知上方程左边含有一个因式，即方程可化为

因此，要A＝B，即要方程

             ①

要么没有实根，要么实根是方程 ②的根.

若①没有实根，则，由此解得 

若①有实根且①的实根是②的实根，则由②有 ，代入①有 2ax＋1＝0.

由此解得，再代入②得 由此解得  .

故 a的取值范围是  

w.w.w.k.s.5.u.c.o.m

www.ks5u.com