高中数学语文版（中职）基础模块上册5.2 弧度制备课ppt课件

这是一份高中数学语文版（中职）基础模块上册5.2 弧度制备课ppt课件，共35页。PPT课件主要包含了问题的提出，利用弧度表示角等内容，欢迎下载使用。

1、角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形其中 正角、负角、零角 分别是怎样规定的？
2、在直角坐标系内讨论角，象限角、轴线角、终边相同的角都是什么样的角？
3、与角α终边相同的角的一般表达式是什么？
S={β|β=α＋k·360°，k∈Z}
物体的长度：可以用米、厘米、英尺、码等不同的单位度量，
【问题一】：度量长度可用哪些不同的单位制？度量质量又可以用哪些不同的单位制？
物体的质量：可以用千克、磅等不同的单位度量.
【问题二】：数学中角度的表示方法有哪些？
度量角的方法: (角度制) 10 —把圆周角平均分为360等份，1份叫1度的角； 1/—1度的角平均分成60等份， 1份叫1分的角； 1//—1分的角平均分成60等份, 1份叫1秒的角.
1、回顾，在初中定义：什么叫1度的角？1 为圆周的 。
一.弧度制的概念
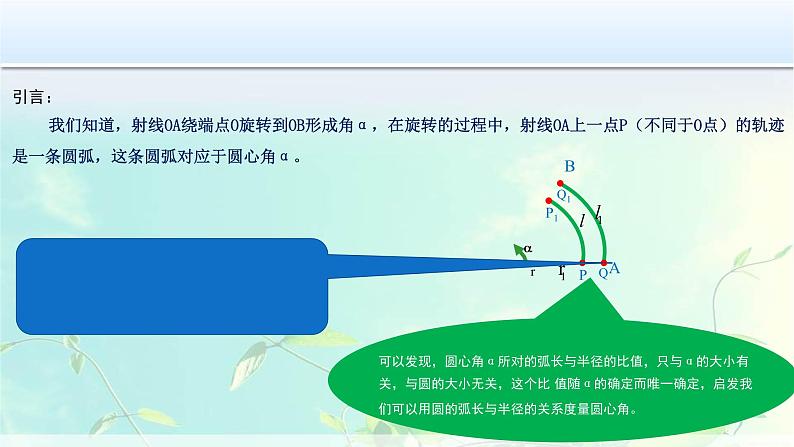
引言： 我们知道，射线OA绕端点O旋转到OB形成角α，在旋转的过程中，射线OA上一点P（不同于O点）的轨迹是一条圆弧，这条圆弧对应于圆心角α。
【弧度制定义】长度等于半径长的圆弧所对的圆心角叫做1弧度的角，弧度单位用rad表示，读作弧度
我们把半径为1的圆叫做单位圆。
1、在单位圆中，当圆心角为周角时，它所对的弧长为2π，所以周角的弧度数为2π，周角是2π rad 的角.2、任意一个00~3600的角的弧度数必然适合不等式 0≤x<2π.3、任一正角的弧度数都是一个正实数； 任一负角的弧度数都是一个负实数； 零角的弧度数是0.以后可以把弧度的单位省略不写：如：1rad=1 -1/3rad=-1/3 2π rad= 2π等等。
例1.下列各命题中，真命题是 A.1弧度就是1°的圆心角所对的弧 B.1弧度是长度等于半径的弧 C.1弧度是1°的弧与1°的角之和 D.1弧度是长度等于半径的弧所对的圆心角的大小
解:　根据弧度制和角度制的规定可知A，B，C均错误，D正确.
(1)圆心角α与所对应的弧长和半径的比值是唯一确定的；
(2)任意角的弧度数与实数是一一对应的关系.
【练1】下列说法正确的是 A.1弧度的圆心角所对的弧长等于半径 B.大圆中1弧度的圆心角比小圆中1弧度的圆心角大 C.所有圆心角为1弧度的角所对的弧长都相等 D.用弧度表示的角都是正角
解：对于A，根据弧度的定义知，“1弧度的圆心角所对的弧长等于半径”，故A正确； 对于B，大圆中1弧度的圆心角与小圆中1弧度的圆心角相等，故B错误； 对于C，只有在同圆或等圆中，1弧度的圆心角所对的弧长是相等的，故C错误； 对于D，用弧度表示的角也可以是负角或零角，故D错误.
二、角度制与弧度制的相互转化
　　用“弧度”与“度”去度量每一个角时，除了零角以外，所得到的量数都是不同的，但它们既然是度量同一个角的结果，二者就可以相互换算,那么，问题来了，怎样换算呢？．
【弧度制下】圆心角为周角时，它所对的弧长为2πr，所以周角的弧度数为2πr/r=2π rad =2π .
【角度制下】圆心角为周角时，周角的度数为3600.
注意点： (1)弧度单位rad可以省略,例如：2rad=2, (2)在同一个题目中，弧度与角度不能混用.
（1）抓住关键式 ： π ＝180°
【例3】　将－1 125°写成α＋2kπ(k∈Z)的形式，其中0≤α<2π，并判断它是第几象限角？
所以－1 125°是第四象限角.
【例4】若在本例的条件下，在[－4π，4π]范围内找出与α终边相同的角的集合.
(1)用弧度制表示终边相同的角2kπ＋α(k∈Z)时， 其中2kπ是π的偶数倍，而不是整数倍.
用弧度制表示终边相同角的两个关注点
(2)注意角度制与弧度制不能混用.
【练3】　(1)用弧度制表示与150°角终边相同的角的集合为
【练3】 (2)终边落在图中阴影部分(包括边界)的角的集合为(用 弧度制表示)_______________________________.
解:(2)结合图象，设终边落在阴影部分的角是α，
四、扇形的弧长与面积公式(弧度制)
【例5】已知扇形的周长为10 cm，面积为4 cm2，求扇形圆心角的弧度数.
解：设扇形圆心角的弧度数为θ(0<θ<2π)，弧长为l cm，半径为R cm，
整理得R2－5R＋4＝0，解得R1＝1，R2＝4.当R＝1时，l＝8，此时，θ＝8 >2π 舍去.
【探究】已知一扇形的周长为4，当它的半径与圆心角取何值时，扇形的面积最大？最大值是多少？
解：设扇形圆心角的弧度数为θ(0<θ<2π)，弧长为l，半径为r，面积为S，
【悟】扇形的弧长和面积的求解策略
(2)找关键：涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题，关键是分析题目中已知 哪些量，求哪些量，然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.
【练4】已知扇形的半径为10 cm，圆心角为60°，求扇形的弧长和面积.
1.知识点： (1)弧度制的概念. (2)弧度与角度的相互转化. (3)掌握特殊角的度数与弧度数的对应关系. (4)扇形的弧长与面积的计算.
2.方法归纳：由特殊到一般、数学运算.
3.易错点：弧度与角度混用.
1、课本P175 练习1-6题。2、补充：已知扇形的周长为10cm, 面积为4cm2,求扇形的中心角的弧度数.