高中数学苏教版选修14.2结构图教案及反思

这是一份高中数学苏教版选修14.2结构图教案及反思，共5页。教案主要包含了工序流程图，程序框图，结构图等内容，欢迎下载使用。

结构图的作用很特别，它不仅可以应用于数学知识的学习，还可以广泛应用在我们日常生活中的方方面面．本文将介绍结构图的三大应用，也许对你全面了解结构图的作用会有帮助．请看：
1．利用结构图，构建知识网络
当某一章节内容学完后，老师为了让我们理清知识脉络，抓住重点，通常会画一个“树形”网络图，其实，这个“树形”图就是我们所学的结构图．它对我们充分认识、掌握知识很有帮助．
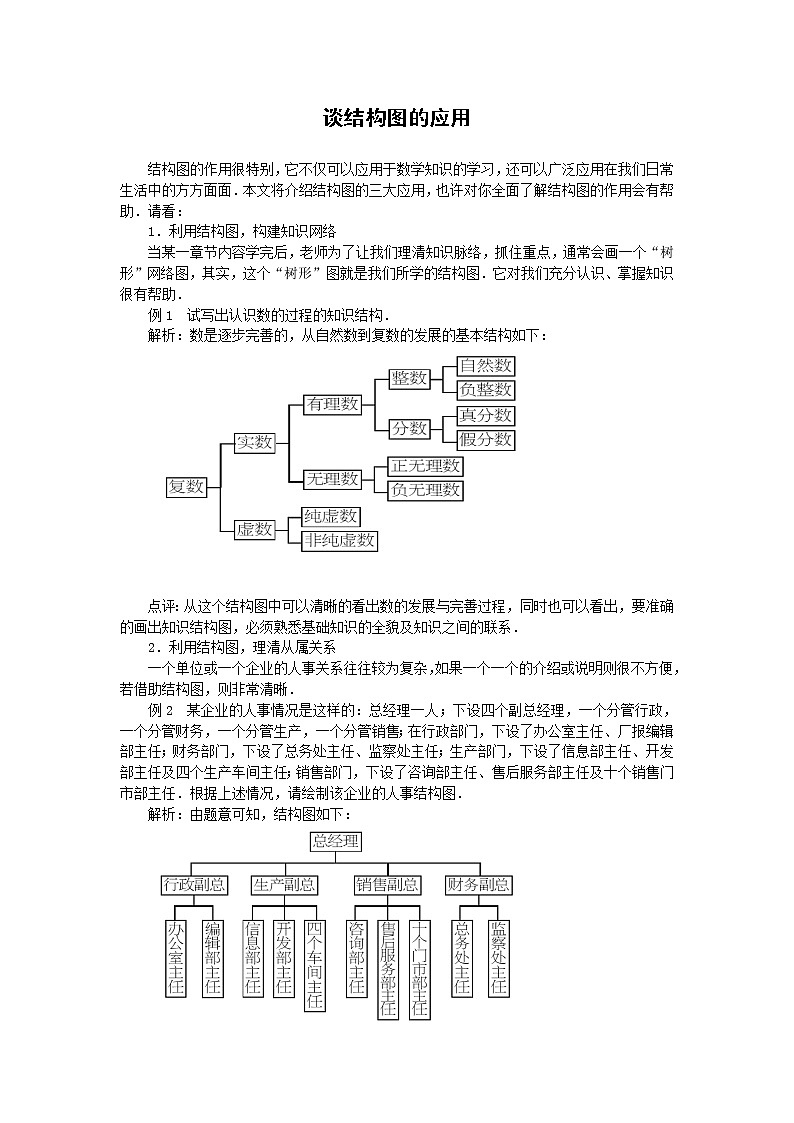
例1 试写出认识数的过程的知识结构．
解析：数是逐步完善的，从自然数到复数的发展的基本结构如下：
点评：从这个结构图中可以清晰的看出数的发展与完善过程，同时也可以看出，要准确的画出知识结构图，必须熟悉基础知识的全貌及知识之间的联系．
2．利用结构图，理清从属关系
一个单位或一个企业的人事关系往往较为复杂，如果一个一个的介绍或说明则很不方便，若借助结构图，则非常清晰．
例2 某企业的人事情况是这样的：总经理一人；下设四个副总经理，一个分管行政，一个分管财务，一个分管生产，一个分管销售；在行政部门，下设了办公室主任、厂报编辑部主任；财务部门，下设了总务处主任、监察处主任；生产部门，下设了信息部主任、开发部主任及四个生产车间主任；销售部门，下设了咨询部主任、售后服务部主任及十个销售门市部主任．根据上述情况，请绘制该企业的人事结构图．
解析：由题意可知，结构图如下：
点评：通过结构图可以很清楚的看出该企业的人事结构，有这样的结构图当然可以提高办事效率．其实，我们学习过的知识中也有很多存在着从属关系，也可以通过结构图将它们显现出来．
3．利用结构图，快速找准位置
现在一栋楼的可用面积越来越大，容纳的单位也越来越多，正常情况下，在一栋大楼的大堂中都会有一个平面图，这个平面图就是结构图．
例3 某行政大楼的二楼是大会议厅；三楼是教育类，其中从左至右是成人教育办公室、特殊教育办公室、小学教育办公室、中学教育办公室、主任办公室；四楼是计生类，从左至右是办证室、外来务工人员登记室、主任室；五楼是安全类，从左至右是消防办公室、安检办公室、主任室；六楼是行政类，从左至右是局长办公室、四个副局长办公室、接待室．请根据上述资料，绘制一个平面图．
解析：从下往上，分别为一楼、二楼、三楼、四楼、五楼、六楼，因此，得结构图如下：
点评：假若你到该行政部门办事，借助这个结构图可以很快找到自己要去的地方，由此可以体会到结构图给我们带来很大的方便．
以上介绍了结构图的三种应用，在实际生活中结构图的应用远不止这三种，只要认真学好该部分知识，你会发现结构图的应用无处不在、无处不有．
框图在实际问题中的应用
框图是表示一个系统各部分和各环节之间关系的图示，它能够清晰地表达比较复杂的系统各部分之间的关系，是表达和交流思想的工具．由于流程图和结构图直观形象、简洁明了，在日常生活中都有着非常重要的应用．下面举例归纳说明．
一、工序流程图
例1 我们生活中用的纸杯从原材料（纸张）到商品（纸杯）主要经过四道工序：淋膜、印刷、模切、成型．首先用淋膜机给原纸淋膜（聚乙烯），然后用分切机把已经淋膜好的纸分切成矩形纸张（印刷后做纸杯壁用）和卷筒纸（纸杯底部用），再将矩形纸印刷并切成扇形杯片，最后成型，请用流程图表示纸杯的加工过程．
分析：画工序流程图应先理清工序大体分几个阶段，再对每一阶段细分，每一步应注意先后顺序，这是十分关键的，否则会产生错误．在画工序流程图时，不能出现几道工序首尾相接的圈图或循环回路．
解：这是一道工序流程图题目，描述纸杯制作的整个过程．由题意得流程图如下：
二、程序框图
我们在数学③中所学过的程序框图，就是一种流程图．现举两个实际生活中的例子．
例2 请根据你的认识，设计一个用电水壶烧两壶开水的方法，并用流程图表示．
解：
例3 某居民区的物业管理部门每月向居民收物业费，计费方法是：3人及3人以下的住户，每户收取6元；超过3人的住户，每超出1人收元．设计一个算法，根据输入的人数，计算应收取的物业费，并画出程序框图．
解：设住房的人数为，每月应交物业费元，则
算法步骤：
第一步：输入；
第二步：如果，则；如果，则；
第三步：输出．
程序框图为：
三、结构图
例4 下面是某电信公司关于账单的表述，试画出账单的结构图．
总体上，账单由客户基本信息、费用、积分、交费记录四部分组成．客户基本信息包括客户姓名、手机号码、话费账期等，以帮助客户核对本账单是否是自己想要的账单；费用部分由当月各项费用组成；积分部分告知客户当前可用积分和累计积分值；交费记录部分提供客户当月（话费账期）交费记录．
其中费用部分是整体账单的核心，也是客户所着重关注的，可以同话费发票对照来看．通常情况下，它由月租费、套餐月基本费、必选包月费、增值业务费、短信通讯费、彩信费、功能费、漫游费、长途费、基本通话费．每个费用项目下有更明细的费用组成．
分析：在画结构图时，需要有较高的抽象概括能力和逻辑思维能力，要熟悉事物的来龙去脉．从头至尾抓住主要脉络进行分解，弄清各步的逻辑关系．在具体绘制时，可按下列过程：①从头至尾抓住主要脉络，分解成若干步；②将每一步提炼成简洁语言放在矩形框内；③各步按逻辑顺序排列并用线段相连．总体上要注意实际问题的逻辑顺序和概念上的从属关系．
虽然本题题干表述文字较多，但很容易获得其脉络：“账单由客户基本信息、费用、积分、交费记录四部分组成”，将每一部分内容逐步细化．
解：账单的结构图为：
例5 试画出数学必修①《集合与函数》这一章的知识结构图．
分析：结构图的主要特点是高度的概括性，利用这一特点可表现知识间的纵横联系，可精炼地概括出一章的知识结构．
解：知识结构图为：