高中数学：3.1《回归分析》（二） 教案 （北师大选修2-3）

3.1回归分析（教案）

教学目标：

1. 通过对统计案例的探究，会对两个随机变量进行线性回归分析.
2. 理解相关系数的含义，会计算两个随机变量的线性相关系数，会通过线性相关系数判断它们之间的线性相关程度.
3. 通过对数据之间散点图的观察，能够对两个随机变量进行可线性化的回归分析.

教学重点:

散点图的画法，回归直线方程的求解方法;相关系数的求法与应用.

教学难点

回归直线方程的求解方法; 相关系数的求法与应用; ；能够对两个随机变量进

行可线性化的回归分析.

教法：启发诱导式

第一课时（回归分析）

教学过程

一、问题情境

  客观事物是相互联系的过去研究的大多数是因果关系，但实际上更多存在的是一种非因果关系比如说：某某同学的数学成绩与物理成绩，彼此是互相联系的，但不能认为数学是“因”，物理是“果”，或者反过来说事实上数学和物理成绩都是“果”，而真正的“因”是学生的理科学习能力和努力程度所以说，函数关系存在着一种确定性关系但还存在着另一种非确定性关系——相关关系

二、新授

在必修课程中，我们已经学习了最小二乘法，并会建立变量之间的线性回归方程.引导学生阅读教材，然后完成知识点的填充.

（一）              知识讲解

1.相关关系的概念

两个变量间的关系可分为确定关系和非确关系，前者又称为函数关系，后者又称为相关关系.

2.回归方程

设有对观测数据，根据线性回归模型，对于每一个，对应的随机偏差项，我们希望总偏差越小越好，即要使越小越好．所以，只要求出使取得最小值时的，值作为，的估计值，记为，．

注：这里的就是拟合直线上的点到点的距离．

用什么方法求，？

回忆《数学3（必修）》“2．4线性回归方程”P71“热茶问题”中求，的方法：最小二乘法．

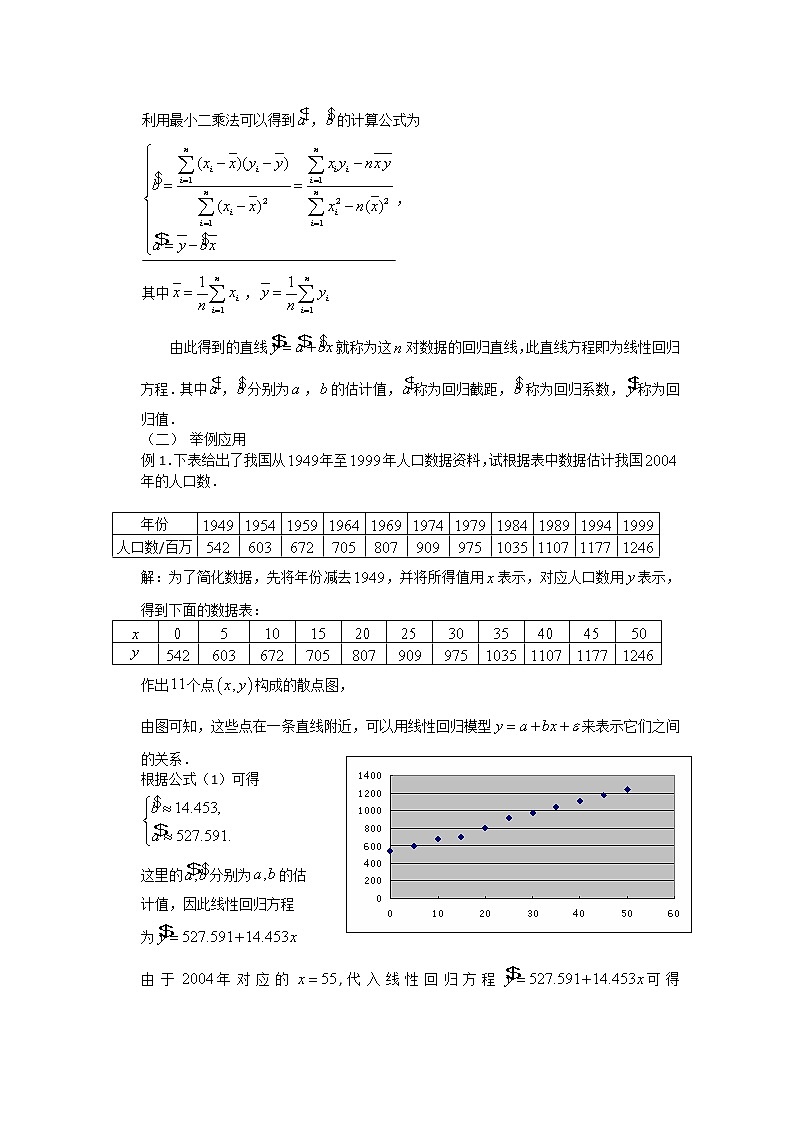
利用最小二乘法可以得到，的计算公式为

，

其中，

由此得到的直线就称为这对数据的回归直线，此直线方程即为线性回归方程．其中，分别为，的估计值，称为回归截距，称为回归系数，称为回归值．

（二）              举例应用

例1．下表给出了我国从年至年人口数据资料，试根据表中数据估计我国年的人口数．

解：为了简化数据，先将年份减去，并将所得值用表示，对应人口数用表示，得到下面的数据表：

作出个点构成的散点图，

由图可知，这些点在一条直线附近，可以用线性回归模型来表示它们之间的关系．

根据公式（1）可得

这里的分别为的估

计值，因此线性回归方程

为

由于年对应的,代入线性回归方程可得（百万），即年的人口总数估计为13.23亿.

对应练习：课本练习

小结：1.线性相关的概念；2.理解回归方程的系数来历；3.求回归方程的步骤.

作业：课本习题1-1，1题的第二问

第二节相关系数

教学过程：

一．问题情境

对任意给定的样本数据，由计算公式都可以求出相应的线性回归方程，但求得的线性回归方程未必有实际意义．左图中的散点明显不在一条直线附近，不能进行线性拟合，求得的线性回归方程是没有实际意义的；右图中的散点基本上在一条直线附近，我们可以粗略地估计两个变量间有线性相关关系，但它们线性相关的程度如何，如何较为精确地刻画线性相关关系呢？为了回答这个问题，我们需要对变量与的线性相关性进行检验（简称相关性检验），那么就需要学习相关系数来处理.

二、新授

（一）知识点讲解

1．相关系数的计算公式：

对于，随机取到的对数据，样本相关系数的计算公式为

．

2．相关系数的性质：

   （1）；

   （2）越接近与1，，的线性相关程度越强；

   （3）越接近与0，，的线性相关程度越弱．

可见，一条回归直线有多大的预测功能，和变量间的相关系数密切相关．

（二）              应用举例

要分析学生高中入学的数学成绩对高一年级数学学习的影响，在高一年级学生中随机抽取名学生，分析他们入学的数学成绩和高一年级期末数学考试成绩如下表：

（1）计算入学成绩与高一期末成绩的相关系数；

（2）如果与之间具有线性相关关系，求线性回归方程；

（3）若某学生入学数学成绩为分，试估计他高一期末数学考试成绩．

解：(1)因为，，

，，

．

因此求得相关系数为．

结果说明这两组数据的相关程度是比较高的；

点评：解决这类问题的解题步骤：

   （1）作出散点图，直观判断散点是否在一条直线附近；

   （2）求相关系数；

   （3）计算，，写出线性回归方程．

对应练习：课本练习

五．回顾小结：

1．相关系数的计算公式与回归系数计算公式的比较；

2．相关系数的性质；

3．探讨相关关系的基本步骤．

六．课外作业：习题1-1第2题．

第三节可线性化的回归分析

教学过程：

一．问题情境

    前面我们学习的是利用线性回归方程与相关系数判断两个随机变量间的相关关系的，那么能否利用散点图将其他的常见函数拟合成线性关系呢？这也是我们本节课将要学习的可线性化的回归分析问题

二、新授

（一）知识点讲解

在实际问题中，有时两个变量之间的关系并不是线性关系，这就需要我们根据专业知识或散点图，对某些特殊的非线性关系，选择适当的变量代换，把非线性方程转化为线性回归方程，从而确定未知参数．下面列举出一些常见的曲线方程，并给出相应的化为线性回归方程的换元公式．

   （1），令，，则有．

   （2），令，，，则有．

   （3），令，，，则有．

   （4），令，，，则有．

   （5），令，，则有．

（二）应用

举例某地区对本地的企业进行了一次抽样调查，下表是这次抽查中所得到的各企业的人均资本（万元）与人均产出（万元）的数据：人均

   （1）设与之间具有近似关系（为常数），试根据表中数据估计和的值；

   （2）估计企业人均资本为万元时的人均产出（精确到）．

分析：根据，所具有的关系可知，此问题不是线性回归问题，不能直接用线性回归方程处理．但由对数运算的性质可知，只要对的两边取对数，就能将其转化为线性关系．

解（1）在的两边取常用对数，可得，设，，，则．相关数据计算如图所示．

仿照问题情境可得，的估计值，分别为由可得，即，的估计值分别为和．

   （2）由（1）知．样本数据及回归曲线的图形如图（见书本 页）

当时，（万元），故当企业人均资本为万元时，人均产值约为万元．

2．练习：练习．

五．回顾小结：

1． 线性回归模型与确定性函数相比，它表示与之间是统计相关关系（非确定性关系）其中的随机误差提供了选择模型的准则以及在模型合理的情况下探求最佳估计值，的工具；

2． 线性回归方程中，的意义是：以为基数，每增加1个单位，相应地平均增加个单位；

3．求线性回归方程的基本步骤．

六．课外作业：第4题．