初中数学鲁教版 (五四制)七年级上册3 简单的轴对称图形集体备课ppt课件

这是一份初中数学鲁教版 (五四制)七年级上册3 简单的轴对称图形集体备课ppt课件，共22页。PPT课件主要包含了角是轴对称图形吗，验证猜想，辨一辨，不必再证全等等内容，欢迎下载使用。
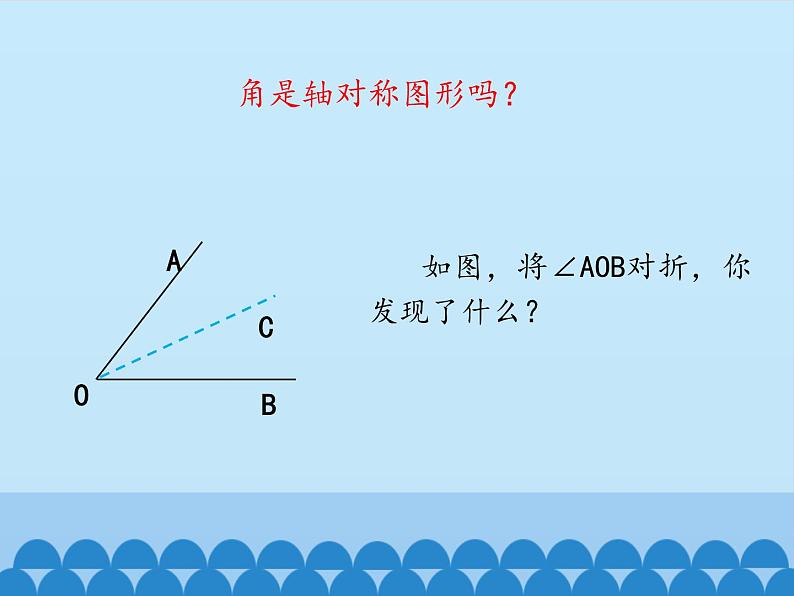
如图，将∠AOB对折，你发现了什么？
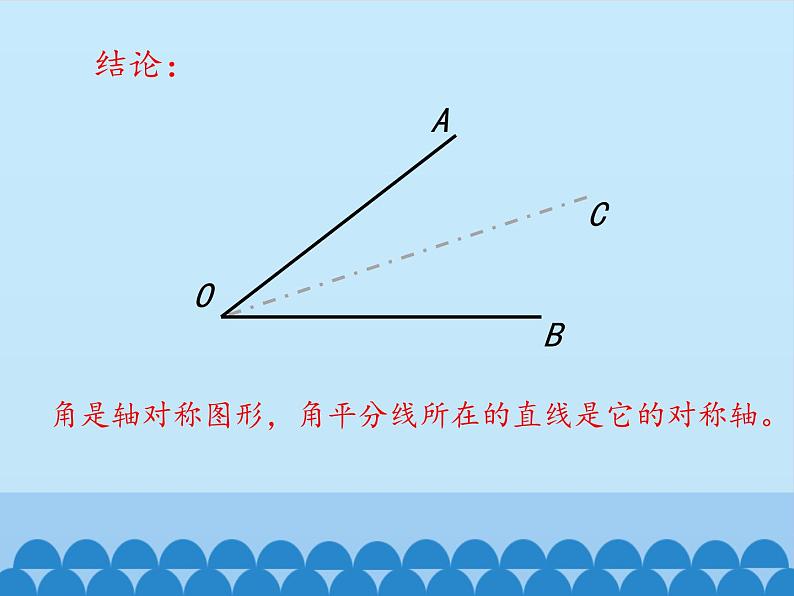
角是轴对称图形，角平分线所在的直线是它的对称轴。
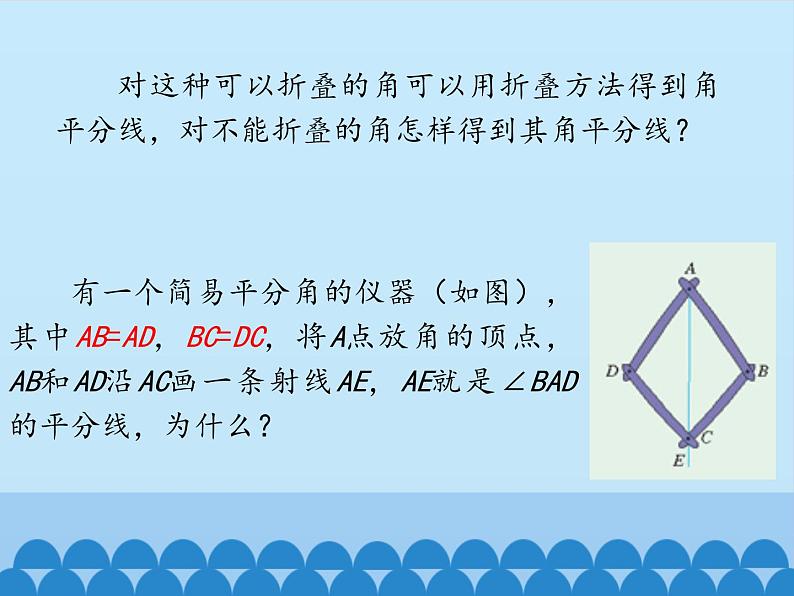
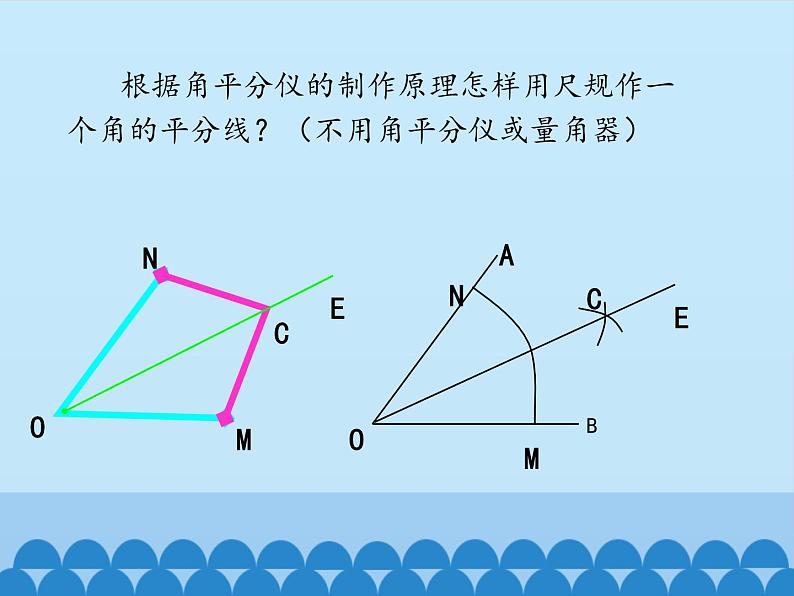
有一个简易平分角的仪器（如图），其中AB=AD，BC=DC，将A点放角的顶点，AB和AD沿AC画一条射线AE，AE就是∠BAD的平分线，为什么？
对这种可以折叠的角可以用折叠方法得到角平分线，对不能折叠的角怎样得到其角平分线？
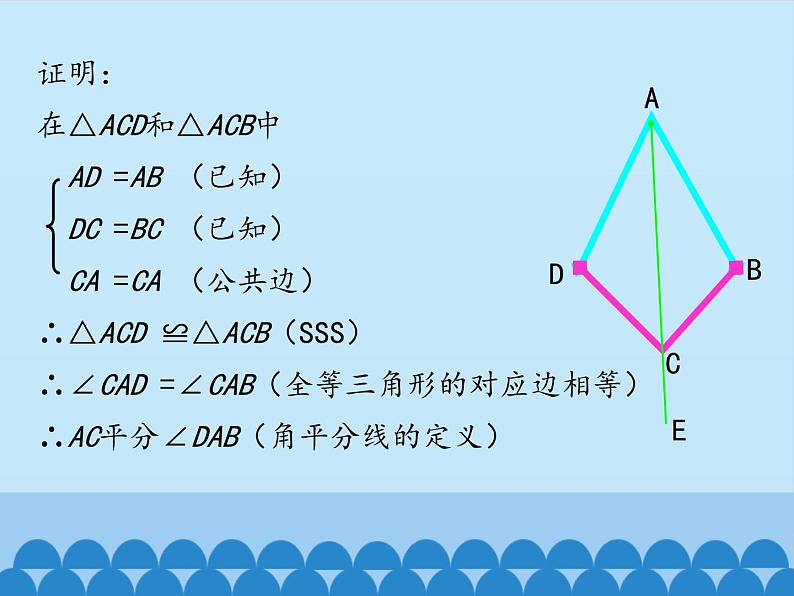
证明：在△ACD和△ACB中 AD =AB （已知） DC =BC （已知） CA =CA （公共边）∴△ACD ≌△ACB（SSS）∴∠CAD =∠CAB（全等三角形的对应边相等）∴AC平分∠DAB（角平分线的定义）
根据角平分仪的制作原理怎样用尺规作一个角的平分线？（不用角平分仪或量角器）
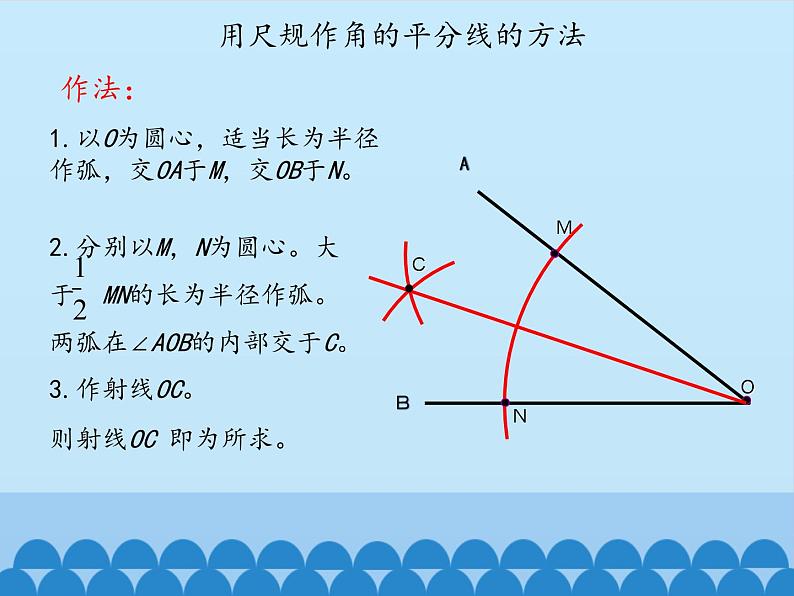
用尺规作角的平分线的方法
1.以O为圆心，适当长为半径作弧，交OA于M，交OB于N。
则射线OC 即为所求。
（1）在一张纸上任意画∠AOB，沿角的两边将角剪下。将这个角对折，使角的两边重合，折痕就是∠AOB的平分线。（2）在∠AOB的角平分线上任意取一点C，分别折出过点C且与∠AOB的两边垂直的直线，垂足分别为D，E。将∠AOB再次对折，折痕CD与CE能重合吗？改变点C的位置，CD和CE还相等吗？
角的平分线上的点到这个角的两边的距离相等。
已知：如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别是D，E。
证明：∵PD⊥OA，PE⊥OB（已知）∴∠PDO=∠PEO=90°（垂直的定义）
在△PDO和△PEO中
∴PD=PE（全等三角形的对应边相等）
∠PDO=∠PEO∠AOC=∠BOCOP=OP
∴△PDO≌△PEO（AAS）
角的平分线上的点到角的两边的距离相等。
角平分线上的点到角两边的距离相等。
利用此性质怎样书写推理过程?
定理：角的平分线上的点到角的两边的距离相等。
∵ ∠1=∠2 PD⊥OA，PE⊥OB∴PD=PE(角的平分线上的点到角的两边的距离相等)
推理的理由有三个，必须写完全，不能少了任何一个。
定理应用所具备的条件：
如图，OC平分∠AOB，PD与PE相等吗？
（1）∵如图，AD平分∠BAC（已知）
∴_____=_____，
(在角的平分线上的点到这个角的两边的距离相等。)
（2）∵如图，DC⊥AC，DB⊥AB（已知）
∴____=____，
（3）∵AD平分∠BAC，DC⊥AC，DB⊥AB（已知）
例2利用尺规，作∠AOB的平分线。已知：∠AOB，如图，求作：射线OC，使∠AOC=∠BOC。作法：（1）在OA和OB上分别截取OD，OE，使OD=OE。（2）分别以D，E为圆心，以大于1/2DE的长度为半径作弧，两弧在∠AOB内交于点C。（3）作射线OC。OC就是∠AOB的平分线。
如图，在Rt△ABC中，∠C=90°，BD是角∠ABC的平分线，DE⊥AB，垂足为E，DE与DC相等吗？为什么？
1.“作已知角的平分线”的尺规作图法；
2.角的平分线的性质：角的平分线上的点到角的两边的距离相等。
∵OC是∠AOB的平分线，又PD⊥OA，PE⊥OB∴PD=PE(角平分线上的点到角的两边距离相等)。
课本习题2.4 问题解决题2