浙教版九年级上册4.4 两个三角形相似的判定教学设计
展开两个三角形相似的判定
【教学目标】
1.知识与技能目标:
(1)理解相似三角形的概念,能正确地找出相似三角形的对应边和对应边角。
(2)掌握相似三角形判定定理的“预备定理”。
2.过程与方法目标:
(1)通过探索相似三角形判定定理的“预备定理”的过程,培养学生的动手操作能力,观察、分析、猜想和归纳能力,渗透类比、转化的数学思想方法。
(2)利用相似三角形的判定定理的“预备定理”进行有关判断及计算,训练学生的灵活运用能力,提高表达能力和逻辑推理能力。
3.情感与态度目标:
(1)通过实物演示和电化教学手段,把抽象问题直观化,激发学生学习的求知欲,感悟数学知识的奇妙无穷。
(2)通过主动探究、合作交流,在学习活动中体验获得成功的喜悦。
【教学重点】
相似三角形判定定理的预备定理的探索。
【教学难点】
相似三角形判定定理的预备定理的有关证明。
【教学方法】
探究法。
【教学过程】
一、教学准备
1.全等三角形的基础知识。
2.三角形中位线定理及其证明方法。
3.平行四边形的判定和性质。
4.相似多边形的定义。
5.比例的性质。
二、复习引入
(一)复习
1.相似图形指的是什么?
2.什么叫做相似三角形?
(二)引入
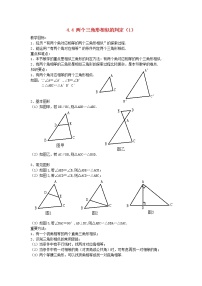
如图1,△ABC与△A’B’C’相似。
图1
记作“△ABC∽△A’B’C’”,读作“△ABC相似于△A’B’C’”。
[注意]:两个三角形相似,用字母表示时,与全等一样,应把表示对应顶点的字母写在对应位置上,这样便于找出相似三角形的对应边和对应边角。
对于△ABC∽△A’B’C’,根据相似形的定义,应有
∠A=∠A’,∠B=∠B’,∠C=∠C’,==。
[问题]:将△ABC与△A’B’C’相似比记为k1,△A’B’C’与△ABC相似比记为k2,那么k1与k2有什么关系?k1=k2能成立吗?
三、探索交流
(一)探究
1.在△ABC中,D为AB的中点,如图2,过D点作DB∥BC交AC于点E,那么△ADE与△ABC相似吗?
(1)“角”
∠BAC=∠DAE。
∵DB∥BC,∴∠ADE=∠B,∠AED=∠C.
(2)“边”
要证明对应边的比相等,有哪些方法?
Ⅰ、直接运用三角形中位线定理及其逆定理
∵DB∥BC,D为AB的中点,
∴E为AC的中点,即DE是△ABC的中位线。
(三角形中位线定理的逆定理)
∴DE=BC.(三角形中位线定理)
∴===。
∴△ADE∽△ABC.
Ⅱ、利用全等三角形和平行四边形知识
过点D作DF∥AC交BC于点F,如图3.
则△ADE≌△ABC,(ASA)
且四边形DFCE为平行四边形。
(两组对边分别平行的四边形是平行四边形)
∴DE=BF=FC.
∴===。
∴△ADE∽△ABC.
2.当D1.D2为AB的三等分点,如图4.过点D1.D2分别作 BC的平行线,交AC于点E1.E2,那么△AD1E1.△AD2E2与△ABC相似吗?
由(1)知△AD1E1∽△AD2E2,下面只要证明△AD1E1与△ABC相似,关键是证对应边的比相等。
过点D1、D2分别作AC的平行线,交BC于点F1.F2,设D1F1与D2F2相交于G点。
则△AD1E1≌△D1D2G≌D2BF2,(ASA)
且四边形D1F1CE1.D2F2CE2.D1GE2E1.D2F2F1G为平行四边形。
(两组对边分别平行的四边形是平行四边形)
∴D1E1=BF2=F2F1=F1C,
∴AE1=E1E2=E2C,
∴===。
∴△AD1E1∽△ABC.
∴△AD1E1∽△AD2E2∽△ABC.
[思考]:上述证明过程较复杂,有较简单的证明方法吗?
过点D2分别作AC的平行线,交BC于点F2,如图5.
则四边形D2F2CE2为平行四边形,
且△AD1E1≌D2BF2,(ASA)
∴D2E2=F2C,D1E1=BF2.
由(1)知,D1E1=D2E2,AE1=AE2,
∴D1E1=BC,AE1=AC.
∴===。
∴△AD1E1∽△ABC.
∴△AD1E1∽△AD2E2∽△ABC.
(二)[猜想]
3.通过上面两个特例,可以猜测:当D为AB上任一点时,如图6,过D点作DE∥BC交AC于点E,都有△ADE与△ABC.
图6
(三)[归纳]定理
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似。
这个定理可以证明,这里从略。
四、应用迁移
[操作]:
练习1.如图案,点D在△ABC的边AB上,DB∥BC交AC于点E。写出所有可能成立的比例式。
练习3.在第1题中,如果=,AC=8cm。求AE长。
初中数学浙教版九年级上册4.4 两个三角形相似的判定优秀教学设计及反思: 这是一份初中数学浙教版九年级上册4.4 两个三角形相似的判定优秀教学设计及反思,共2页。教案主要包含了复习回顾,探究新知,巩固应用,课堂小结,布置作业,反思等内容,欢迎下载使用。
初中数学浙教版九年级上册4.4 两个三角形相似的判定优秀教学设计及反思: 这是一份初中数学浙教版九年级上册4.4 两个三角形相似的判定优秀教学设计及反思,共2页。教案主要包含了复习回顾,探究新知,巩固应用,课堂小结,布置作业,反思等内容,欢迎下载使用。
初中数学浙教版九年级上册第4章 相似三角形4.4 两个三角形相似的判定优秀教案: 这是一份初中数学浙教版九年级上册第4章 相似三角形4.4 两个三角形相似的判定优秀教案,共3页。教案主要包含了复习,新课,探究活动,小结等内容,欢迎下载使用。