

2021-2022学年苏科版八年级上册数学期末模拟测试卷(3)(word版 含答案)
展开2021-2022学年上学期八年级数学期末模拟测试卷(3)
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.在,,π,1.010010001四个实数中,无理数有( )
A.1个 B.2个 C.3个 D.4个
3.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
4.在满足下列条件的△ABC中,不是直角三角形的是( )
A.AB:AC:BC=:: B.BC2﹣AB2=AC2
C.∠A:∠B:∠C=3:4:5 D.∠A﹣∠B=∠C
5.在平面直角坐标系中,已知点A(1,3),将点A向左平移3个单位后,再将它向上平移4个单位,则它的坐标变为( )
A.(﹣2,7) B.(4,﹣1) C.(4,7) D.(﹣2,﹣1)
6.如图,在7×7的方格纸中,每个小方格都是边长为1的小正方形,网格线的交点称格点,点A,点B是方格纸中的两个格点,找出格点C,使△ABC的面积为3,则满足条件的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
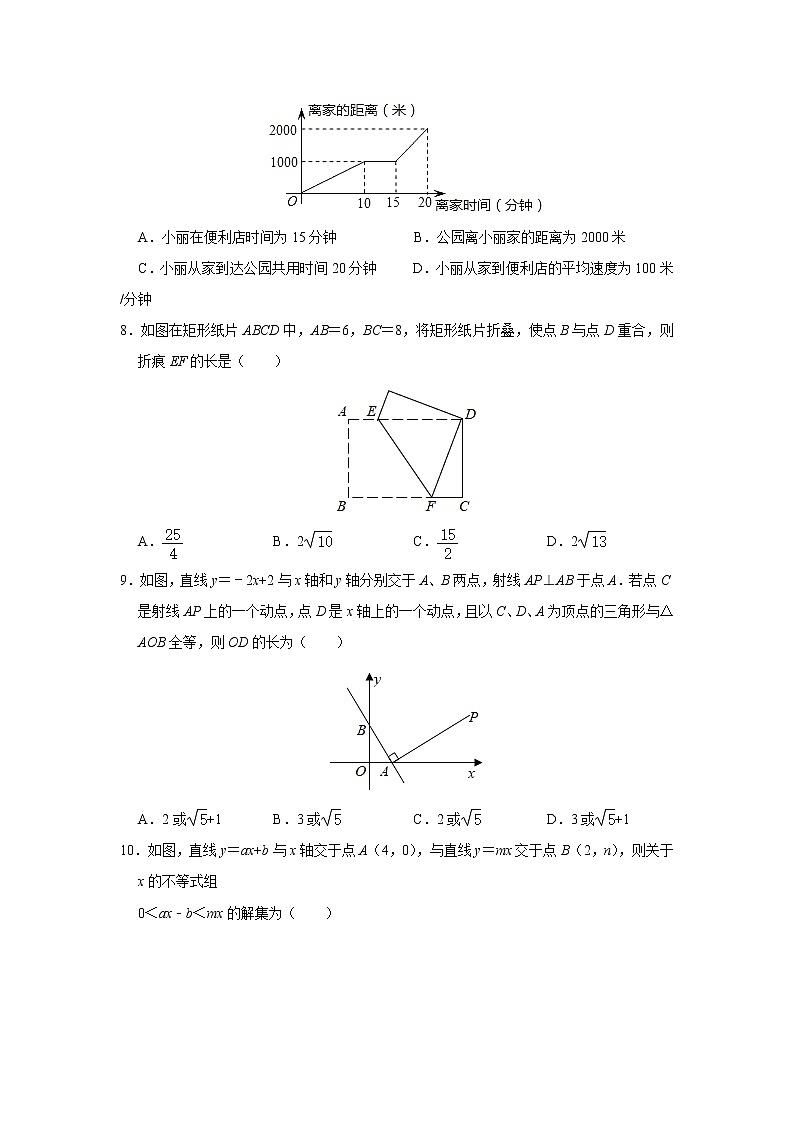
7.周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
A.小丽在便利店时间为15分钟 B.公园离小丽家的距离为2000米
C.小丽从家到达公园共用时间20分钟 D.小丽从家到便利店的平均速度为100米/分钟
8.如图在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,则折痕EF的长是( )
A. B.2 C. D.2
9.如图,直线y=﹣2x+2与x轴和y轴分别交于A、B两点,射线AP⊥AB于点A.若点C是射线AP上的一个动点,点D是x轴上的一个动点,且以C、D、A为顶点的三角形与△AOB全等,则OD的长为( )
A.2或+1 B.3或 C.2或 D.3或+1
10.如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组
0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
11.若x3=﹣,则x的值为 .
12.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
13.若一次函数y=ax﹣b的图象过点A(﹣1,﹣2),则a+b= .
14.已知三角形三边长分别为5,12,13,则此三角形的最大边上的高等于 .
15.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则(m+n)2021的值是 .
16.如图,将△ABC绕点A旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC= °.
17.如图,在平面直角坐标系中,直线分别交x轴、y轴于A、B两点,点P(m,1)在△AOB的内部(不包含边界),则m的取值范围是 .
18.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC,若AC=10,则四边形ABCD的面积为 .
三、解答题(本大题共10小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(4分)计算:|﹣5|+(﹣2)2+﹣﹣1.
20.(5分)已知:BE⊥CD,BE=DE,EC=EA.
求证:
(1)(3分)△BEC≌△DEA;
(2)(2分)DF⊥BC.
21.(4分)如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长.
22.(5分)已知正比例函数的图象经过点(﹣,2).
(1)(3分)求该函数的解析式;
(2)(2分)如果点M(2m,3m+1)在该函数图象上,求m的值.
23.(6分)△ABC在平面直角坐标系中的位置如图所示,A(2,4),B(1,1),C(3,2)三点在格点上.
(1)(2分)作出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标为 ;
(2)(1分)△ABC的面积为 ;
(3)(3分)在y轴上作点P,使得PA+PB最小,请求出点P的坐标,并说明理由.
24.(5分)已知在直角三角形ABC中,∠BAC=90°,AD⊥BC于D,点E是BC的中点,AB=8,AC=6,BC=10.
(1)(3分)求△ABE的面积.
(2)(2分)求AD的长.
25.(5分)如图,直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两直线的交点为P.
(1)(2分)求A、B两点的坐标;
(2)(3分)△ABP的面积.
26.(7分)某电脑销售公司在5月份售出甲、乙、丙三种型号的电脑若干台,每种型号的电脑不少于10台.这个月的支出包括以下三项:这批产品的进货总成本850000元,人员工资和其他支出.这三种电脑的进价和售价如表所示,人员工资y1(元)与总销售量x(台)的关系式为y1=400x+12000,其他支出y2(元)与总销售量x(台)的函数图象如图所示.
型号
甲
乙
丙
进价(元/台)
4500
6000
5500
售价(元/台)
6000
8000
6500
(1)(2分)求其他支出y2(元)与总销售量x(台)的函数关系式;
(2)(2分)如果该公司5月份的人员工资和其他支出共90000元,求该公司5月份共售出甲、乙、丙三种型号的电脑多少台?
(3)(3分)在(2)的条件下,求该公司5月份销售甲、乙、丙三种产品总利润W的最大值,并求出此时三种电脑各销售了多少台?(利润=售价﹣进价﹣人员工资﹣其他支出)
27.(11分)如图,直线y=4﹣x与两坐标轴分别相交于A、B两点,过线段AB上一点M分别作MC⊥OA于点C,MD⊥OB于点D,且四边形OCMD为正方形.
(1)(2分)正方形OCMD的边长为 .
(2)(8分)将正方形OCMD沿着x轴的正方向移动,得正方形EFGH,设平移的距离为a(0<a≤4).
①(3分)当平移距离a=1时,正方形EFGH与△AOB重叠部分的面积为 ;
②(6分)当平移距离a为多少时,正方形EFGH的面积被直线AB分成1:3两个部分?
28.(12分)综合与探究
我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的Rt△ABC纸片(∠B=90°,AB=6,BC=8)并进行探究:
(1)(4分)如图2,“奋斗”小组将Rt△ABC纸片沿DE折叠,使点C落在△ABC外部的C'处.
①若∠1=40°,∠C=37°,则∠2的度数为 .
②∠1,∠2,∠C之间的数量关系为 .
(2)(2分)如图3,“勤奋”小组将△ABC沿DE折叠,使点C与点A重合,求BD的长;
(3)(6分)如图4,“雄鹰”小组将△ABC沿AD折叠,使点B落在点E处,连接CE,当△CDE为直角三角形时,求BD的长.
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
解:A、不是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项符合题意;
D、不是轴对称图形,故此选项不合题意.
答案:C.
2.在,,π,1.010010001四个实数中,无理数有( )
A.1个 B.2个 C.3个 D.4个
解:在,,π,1.010010001四个实数中,无理数有,π,共2个.
答案:B.
3.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
答案:D.
4.在满足下列条件的△ABC中,不是直角三角形的是( )
A.AB:AC:BC=:: B.BC2﹣AB2=AC2
C.∠A:∠B:∠C=3:4:5 D.∠A﹣∠B=∠C
解:A、设AB=k,则AC=k,BC=k,∵AB2+AC2=k2+2k2=3k2=(k)2=BC2,∴△ABC是直角三角形;
B、∵BC2﹣AB2=AC2,∴AB2+AC2=BC2,∴△ABC是直角三角形;
C、∵∠A:∠B:∠C=3:4:5,∴∠C=×180°=75°≠90°,∴△ABC不是直角三角形;
D、∵∠A﹣∠B=∠C,∠A+∠B+∠C=180°,∴∠A=90°,∴△ABC是直角三角形;
答案:C.
5.在平面直角坐标系中,已知点A(1,3),将点A向左平移3个单位后,再将它向上平移4个单位,则它的坐标变为( )
A.(﹣2,7) B.(4,﹣1) C.(4,7) D.(﹣2,﹣1)
解:∵点A(1,3)先向左平移3个单位后,再将它向上平移4个单位,
∴平移后的点的横坐标是1﹣3=﹣2,
纵坐标是3+4=7,
∴坐标变为(﹣2,7).
答案:A.
6.如图,在7×7的方格纸中,每个小方格都是边长为1的小正方形,网格线的交点称格点,点A,点B是方格纸中的两个格点,找出格点C,使△ABC的面积为3,则满足条件的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
解:满足条件的C点有6个,平行于AB的直线上,与网格的所有交点就是.
答案:C.
7.周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
A.小丽在便利店时间为15分钟
B.公园离小丽家的距离为2000米
C.小丽从家到达公园共用时间20分钟
D.小丽从家到便利店的平均速度为100米/分钟
解:小丽在便利店时间为15﹣10=5(分钟),故选项A错误,
公园离小丽家的距离为2000米,故选项B正确,
小丽从家到达公园共用时间20分钟,故选项C正确,
小丽从家到便利店的平均速度为:2000÷20=100米/分钟,故选项D正确,
答案:A.
8.如图在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,则折痕EF的长是( )
A. B.2 C. D.2
解:连接BE,BD,设EF与BD相交于点O,如图,
∵矩形ABCD纸片折叠,使点D与点B重合,
∴EF垂直平分BD,∠BFE=∠DFE,
∴ED=EB,FD=FB,EF⊥BD,
∴∠EDB=∠EBD,
∵AD∥BC,
∴∠DEF=∠BFE,
∴∠DEF=∠DFE,
∴DF=DE,
∴DE=EB=BF=FD,
∴四边形DEBF为菱形,
在Rt△ABD中,BD===10,
设BE=x,则DE=x,AE=8﹣x,
在Rt△ABE中,AB2+AE2=DE2,
∴62+(8﹣x)2=x2,
解得x=,
∴BE=,
∵S菱形DEBF=S三角形DEB
∴×EF•DB=DE•AB,
∴×EF×10=6×,
∴EF=,
答案:C.
9.如图,直线y=﹣2x+2与x轴和y轴分别交于A、B两点,射线AP⊥AB于点A.若点C是射线AP上的一个动点,点D是x轴上的一个动点,且以C、D、A为顶点的三角形与△AOB全等,则OD的长为( )
A.2或+1 B.3或 C.2或 D.3或+1
解:∵AP⊥AB,
∴∠BAP=∠AOB=90°,
∴∠ABO+∠BAO=∠CAD+∠BAO=90°,
∴∠ABO=∠CAD,
在y=﹣2x+2中,
令x=0,则y=2,令y=0,则x=1,
∴OA=1,OB=2,由勾股定理得AB=,
①当∠ACD=90°时,如图1,
∵△AOB≌△DCA,
∴AD=AB=,
∴OD=1+;
②当∠ADC=90°时,如图2,
∵△AOB≌△CDA,
∴AD=OB=2,
∴OA+AD=3,
综上所述:OD的长为1+或3.
答案:D.
10.如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
解:直线y=ax+b经过第一、三、四象限,则a>0,
把A(4,0)代入y=ax+b得4a+b=0,则b=﹣4a,
把B(2,n)代入y=ax+b得n=2a+b=2a﹣4a=﹣2a,
把B(2,n)代入y=mx得n=2m,则m=﹣a,
不等式组0<ax﹣b<mx化为0<ax+4a<﹣ax,
解得﹣4<x<﹣2.
答案:A.
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
11.若x3=﹣,则x的值为 .
解:∵,
∴x的值为.
答案:.
12.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 14 .
解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
答案:14.
13.若一次函数y=ax﹣b的图象过点A(﹣1,﹣2),则a+b= 2 .
解:∵一次函数y=ax﹣b的图象过点A(﹣1,﹣2),
∴﹣2=a×(﹣1)﹣b,
化简,得
a+b=2,
答案:2.
14.已知三角形三边长分别为5,12,13,则此三角形的最大边上的高等于 .
解:∵52+122=132,
∴根据勾股定理的逆定理,△ABC是直角三角形,最长边是13,
设斜边上的高为h,则
S△ABC=×5×12=×13h,
解得:h=,
答案:.
15.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则(m+n)2021的值是 1 .
解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3,1﹣n=2,
解得:m=2,n=﹣1,
所以m+n=2﹣1=1,
所以(m+n)2021=12021=1.
答案:1.
16.如图,将△ABC绕点A旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC= 65 °.
解:∵将△ABC绕点A旋转到△AEF的位置,
∴AB=AE,∠B=70°,
∴∠BAE=180°﹣70°×2=40°,
∴∠FAG=∠BAE=40°.
∵将△ABC绕点A旋转到△AEF的位置,
∴△ABC≌△AEF,
∴∠F=∠C=25°,
∴∠FGC=∠FAG+∠F=40°+25°=65°.
答案:65.
17.如图,在平面直角坐标系中,直线分别交x轴、y轴于A、B两点,点P(m,1)在△AOB的内部(不包含边界),则m的取值范围是 0<m<4 .
解:作直线y=1交y轴于C,交直线AB于D,如图:
在y=﹣x+3中,当y=1时,1=﹣x+3,
解得x=4,即D(4,1),
∵点P(m,1)在△AOB的内部(不包含边界),
∴P(m,1)在线段CD上(不含C、D),
∴0<m<4,
答案:0<m<4.
18.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC,若AC=10,则四边形ABCD的面积为 50 .
解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N,
∵∠BAD=∠BCD=90°,
∴四边形AMCN为矩形,∠MAN=90°,
∵∠BAD=90°,
∴∠BAM=∠DAN,
在△ABM与△ADN中,
,
∴△ABM≌△ADN(AAS),
∴AM=AN;
∴△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
设AM=a,由勾股定理得:AC2=AM2+MC2,而AC=10;
∴2a2=100,a2=50,
所以四边形ABCD的面积为50.
答案:50.
三、解答题(本大题共10小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.计算:|﹣5|+(﹣2)2+﹣﹣1.
解:原式=5+4+(﹣3)﹣2﹣1=9+(﹣6)=3.
20.已知:BE⊥CD,BE=DE,EC=EA.
求证:(1)△BEC≌△DEA;
(2)DF⊥BC.
解:(1)证明:∵BE⊥CD,
∴∠BEC=∠DEA=90°,
在△BEC和△DEA中,
,
∴△BEC≌△DEA(SAS);
(2)∵△BEC≌△DEA,
∴∠B=∠D.
∵∠D+∠DAE=90°,∠DAE=∠BAF,
∴∠BAF+∠B=90°.
即DF⊥BC.
21.如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长.
解:在Rt△ABC中,∠C=90°,AC=8,AB=10,
∴BC===6,
连接BE,
∵DE垂直平分AB,
∴AE=BE,
设AE=BE=x,则CE=8﹣x,
在Rt△BCE中,∵BC2+CE2=BE2,
∴62+(8﹣x)2=x2,
解得x=,
∴AE=.
22.已知正比例函数的图象经过点(﹣,2).
(1)求该函数的解析式;
(2)如果点M(2m,3m+1)在该函数图象上,求m的值.
解:(1)设这个正比例函数的解析式为y=kx,由题意得:
2=﹣k,
解得:k=﹣2.
∴这个正比例函数的解析式为y=﹣2x.
(2)∵点M(2m,3m+1)在函数y=﹣2x图象上,
∴﹣2×2m=3m+1.
解得:m=1.
答:m的值为1.
23.△ABC在平面直角坐标系中的位置如图所示,A(2,4),B(1,1),C(3,2)三点在格点上.
(1)作出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标为 (2,﹣4) ;
(2)△ABC的面积为 ;
(3)在y轴上作点P,使得PA+PB最小,请求出点P的坐标,并说明理由.
解:(1)如图所示,△A1B1C1即为所求,点A1的坐标为(2,﹣4).
答案:(2,﹣4);
(2)△ABC的面积为2×3﹣×1×2×2﹣×1×3=,
答案:;
(3)如图所示,点P即为所求,
点B关于y轴的对称点B2坐标为(﹣1,1),
设AB2所在直线解析式为y=kx+b,
则,
解得,
∴AB2所在直线解析式为y=x+2,
当x=0时,y=2,
∴点P坐标为(0,2),
根据轴对称的性质知PB=PB2,
由两点之间线段最短知PA+PB2最小,
∴PB+PA最小.
24.已知在直角三角形ABC中,∠BAC=90°,AD⊥BC于D,点E是BC的中点,AB=8,AC=6,BC=10.
(1)求△ABE的面积.
(2)求AD的长.
解:(1)∵AB=8,AC=6,BC=10.
∴AB2+AC2=BC2,
∴∠CAB=90°,
∴S△ABC==24,
∵点E是BC的中点,
∴△ABE的面积=S△ABC=12;
(2)∵AD⊥BC,
∴S△ABC=BC•AD=AC•AB,
∴AD==4.8.
25.如图,直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两直线的交点为P.
(1)求A、B两点的坐标;
(2)△ABP的面积.
解:(1)令x=0,得y1=1,y2=﹣2
∴A(0,1),B(0,﹣2);
(2)由,解得,
所以P(﹣1,﹣1);
则 S△APB=(1+2)×1=.
26.某电脑销售公司在5月份售出甲、乙、丙三种型号的电脑若干台,每种型号的电脑不少于10台.这个月的支出包括以下三项:这批产品的进货总成本850000元,人员工资和其他支出.这三种电脑的进价和售价如表所示,人员工资y1(元)与总销售量x(台)的关系式为y1=400x+12000,其他支出y2(元)与总销售量x(台)的函数图象如图所示.
型号
甲
乙
丙
进价(元/台)
4500
6000
5500
售价(元/台)
6000
8000
6500
(1)求其他支出y2(元)与总销售量x(台)的函数关系式;
(2)如果该公司5月份的人员工资和其他支出共90000元,求该公司5月份共售出甲、乙、丙三种型号的电脑多少台?
(3)在(2)的条件下,求该公司5月份销售甲、乙、丙三种产品总利润W的最大值,并求出此时三种电脑各销售了多少台?(利润=售价﹣进价﹣人员工资﹣其他支出)
解:(1)设y2(元)与总销售量x(台)的函数关系式为y2=kx+b,
根据题意得:,
解得:
∴y2(元)与总销售量x(台)的函数关系式为y2=100x+3000;
(2)由题意得:y1+y2=90000,
∴400x+12000+100x+3000=90000,
解得:x=150
该公司5月份共售出甲、乙、丙三种型号的电脑150台;
(3)设该公司5月份销售甲种电脑t台,乙种电脑p台,则售出丙种电脑(150﹣t﹣p)台,
由题意得:4500t+6000p+5500(150﹣t﹣p)=850000,
解得:p=2t+50,
∵每种型号的电脑不少于10台,
∴
∴10≤t≤30,
∴W=6000t+8000(2t+50)+6500(150﹣t﹣2t﹣50)﹣850000﹣90000=2500t+110000(10≤t≤30).
∴当t=30时,W有最大值,最大值为:2500×30+110000=185000(元).
∴2t+50=110(台),150﹣t﹣2t﹣50=10(台).
∴该公司5月份销售甲、乙、丙三种产品总利润W的最大值为185000元,此时甲种电脑销售了30台,乙种电脑销售了110台,丙种电脑销售了10台.
27.如图,直线y=4﹣x与两坐标轴分别相交于A、B两点,过线段AB上一点M分别作MC⊥OA于点C,MD⊥OB于点D,且四边形OCMD为正方形.
(1)正方形OCMD的边长为 2 .
(2)将正方形OCMD沿着x轴的正方向移动,得正方形EFGH,设平移的距离为a(0<a≤4).
①当平移距离a=1时,正方形EFGH与△AOB重叠部分的面积为 ;
②当平移距离a为多少时,正方形EFGH的面积被直线AB分成1:3两个部分?
解:(1)设点M(x,4﹣x),
∵当四边形OCMD为正方形时,OC=CM,即x=4﹣x,
∴x=2,
∴CM=OC=2,
答案:2;
(2)①∵直线AB的解析式为y=﹣x+4,
∴移动过程中正方形EFGH被分割出的三角形是等腰直角三角形,
如图1,
∵四边形EFGH是正方形,
∴正方形EFGH的面积=22=4,
当a=1时,EM=1,
∴S△MQE=EM2=,
∴正方形EFGH与△AOB重叠部分的面积=4﹣=;
答案:;
②∵正方形EFGH的面积被直线AB分成1:3两个部分,
∴两部分的面积分别为1和3.
当0<a≤2时,如图2所示:
∵直线AB的解析式为y=4﹣x,
∴∠BAO=45°,
∴△MQE为等腰直角三角形,
∴EQ=ME,
∴ME2=1,
∴ME=,即a=,
当2<a<4时,如图3所示:
∵∠BAO=45°,
∴△AGQ为等腰直角三角形.
∴GQ=GA.
∴GA2=1,解得:GA=.
∵将y=0代入y=4﹣x得:4﹣x=0,
∴x=4,
∴OA=4.
∴OG=4﹣,即a=4﹣.
综上所述,当平移的距离为a=或a=4﹣时,正方形EFGH的面积被直线AB分成1:3两个部分.
28.综合与探究
我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的Rt△ABC纸片(∠B=90°,AB=6,BC=8)并进行探究:
(1)如图2,“奋斗”小组将Rt△ABC纸片沿DE折叠,使点C落在△ABC外部的C'处.
①若∠1=40°,∠C=37°,则∠2的度数为 114° .
②∠1,∠2,∠C之间的数量关系为 ∠2=∠1+2∠C .
(2)如图3,“勤奋”小组将△ABC沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将△ABC沿AD折叠,使点B落在点E处,连接CE,当△CDE为直角三角形时,求BD的长.
解:(1)①由折叠性质可得∠C=∠C′=37°,
∴∠DFC=∠1+∠C′=77°,
∴∠2=∠DFC+∠C=77+37=114°,
答案:114°;
②由折叠性质可得∠C=∠C′,
∴∠DFC=∠1+∠C′,
∴∠2=∠DFC+∠C=∠1+∠C′+∠C=∠1+2∠C,
答案:∠2=∠1+2∠C;
(2)∵∠B=90°,AB=6,BC=8,
设BD=x,则CD=AD=8﹣x,
在Rt△ABD中,x2+62=(8﹣x)2,
解得:,
∴BD的长为;
(3)在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC==10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8﹣x,
∴CE=AC﹣AE=4,
∴DE2+CE2=CD2,
即x2+42=(8﹣x)2,
解得:x=3,即BD=3;
②如图,当∠EDC=90°,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
2021-2022学年苏科版九年级上学期数学期末模拟卷(4)(word版 含答案): 这是一份2021-2022学年苏科版九年级上学期数学期末模拟卷(4)(word版 含答案),共28页。
2021-2022学年苏科版七年级上学期数学期末模拟卷(3)(含答案): 这是一份2021-2022学年苏科版七年级上学期数学期末模拟卷(3)(含答案),共16页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年苏科版八年级上学期数学期末模拟测试卷(1)(word版 含答案): 这是一份2021-2022学年苏科版八年级上学期数学期末模拟测试卷(1)(word版 含答案),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












