




还剩8页未读,
继续阅读
5.3.1 第2课时 平行线的性质和判定及其综合运用课件PPT
展开
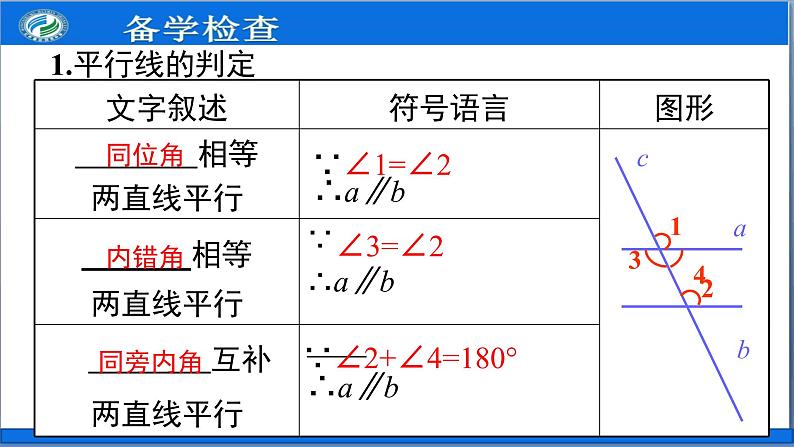
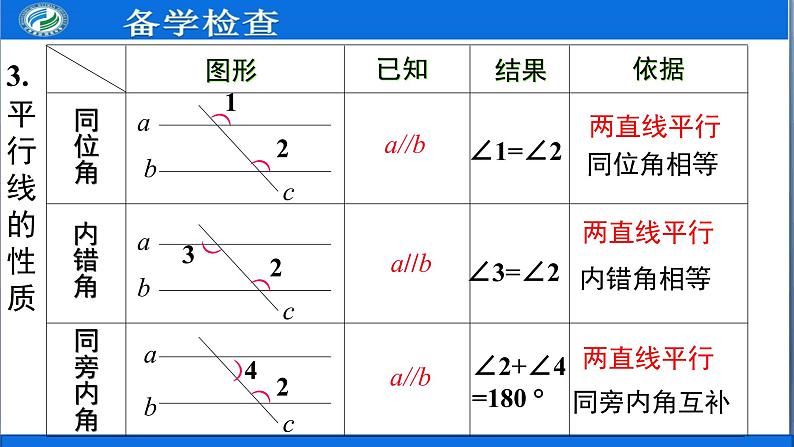
5.3.1 平行线的性质第2课时 平行线的性质和判定及其综合运用学习目标1.进一步熟悉平行线的判定方法和性质;2.运用平行线的性质和判定进行简单的推理和计算;(重点、难点)3.善于总结经验是认识和把握规律的前提和基础,是党发扬成绩、纠正错误、提高自己的重要方法,也是党的优良传统.同位角内错角同旁内角∵∠1=∠2∠3=∠2∵∠2+∠4=180°abc141.平行线的判定导入新课 方法4:如图1,若a∥b,b∥c,则a∥c.( ) 方法5:如图2,若a⊥b,a⊥c,则b∥c.( )平行于同一条直线的两条直线平行 垂直于同一条直线的两条直线平行2.平行线的其它判定方法图形已知结果依据同位角内错角同旁内角122324))))))abababccca//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行3.平行线的性质∠1=∠2∠3=∠2∠2+∠4=180 °① ∵ ∠1 =_____(已知) ∴ AB∥CE② ∵ ∠1 +_____=180o(已知) ∴ CD∥BF③ ∵ ∠1 +∠5 =180o(已知) ∴ _____∥_____.ABCE∠2④ ∵ ∠4 +_____=180o(已知) ∴ CE∥AB∠3∠3(内错角相等,两直线平行)(同旁内角互补,两直线平行)(同旁内角互补,两直线平行)(同旁内角互补,两直线平行)例2 已知∠3=45 °,∠1与∠2互余,试说明AB//CD. 解:由于∠1与∠2是对顶角,∴∠1=∠2.又∵∠1+∠2=90°(已知),∴∠1=∠2=45°.∵ ∠3=45°(已知),∴∠ 2=∠3.∴ AB∥CD(内错角相等,两直线平行).例3 如图,AB//CD,∠A=100°, ∠C=110°, 求∠AEC的度数. 21CDEF121280807070150F解:过点E作EF//AB.∵AB//CD,EF//AB(已知),∴ // (平行于同一直线的两直线平行).∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).又∵∠A=100°,∠C=110°(已知), ∴∠ = °, ∠ = °(等量代换).∴∠AEC=∠1+∠2= °+ ° = °. 2.直线a,b与直线c相交,给出下列条件: ①∠1= ∠2; ②∠3= ∠6; ③∠4+∠7=180o; ④∠3+ ∠5=180°,其中能判断a//b的是( )A. ①②③④ B .①③④ C. ①③ D. ④B解:过点C作CF∥AB,则 _______( )又∵AB∥DE,AB∥CF,∴____________( )∴∠E=∠____( )∴∠B+∠E=∠1+∠2即∠B+∠E=∠BCE.3.已知AB∥DE,试问∠B、∠E、∠BCE有什么关系. 请完成填空: CF∥DE平行于同一直线的两条直线互相平行2两直线平行,内错角相等∠B=∠1两直线平行,内错角相等ABCDE4.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.解:∵∠1=∠2∴AB∥EF(内错角相等,两直线平行).(已知),∵AB⊥BF,CD⊥BF,∴AB∥CD∴EF∥CD∴ ∠3= ∠E(垂直于同一条直线的两条直线平行).(平行于同一条直线的两条直线平行). (两直线平行,内错角相等).5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.解:∵EF∥AD,(已知) ∴∠2=∠3.又∵∠1=∠2,∴∠1=∠3.∴DG∥AB.∴∠BAC+∠AGD=180°.∴∠AGD=180°-∠BAC=180°-70°=110°.(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)(两直线平行,同旁内角互补)拓展提升:如图,AB//CD,试解决下列问题:(1)如图1,∠1+∠2=___ ___;(2)如图2,∠1+∠2+∠3=___ __;(3)如图3,∠1+∠2+∠3+∠4=_ __ __;(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n = ;180°360°540°180°×(n-1)图1图2图3图4判定:已知角的关系得平行的关系.推平行,用判定.性质:已知平行的关系得角的关系.知平行,用性质.平行线的“判定”与“性质”有什么不同:课堂小结
相关资料
更多









