高二数学知能优化训练 湘教版必修5：13.2.2 《几何概率》

1．下列概率模型中，几何概率的个数为(　　)

①从区间[－10,10]内任取出一个数，求取到1的概率；

②从区间[－10,10]内任取出一个数，求取到绝对值不大于1的数的概率；

③从区间[－10,10]内任取出一个整数，求取到大于1而小于2的数的概率；

④向一个边长为4 cm的正方形ABCD内投一点P，求点P离中心不超过1 cm的概率．

A．1　　　　　　　　　　　　 B．2

C．3   D．4

解析：选B.①不是几何概率，虽然区间[－10,10]有无限多个点，但取到“1”只是一个数字，不能构成区域长度；

②是几何概率，因为区间[－10,10]和[－1,1]上有无限多个数可取(满足无限性)，且在这两个区间内每个数被取到的机会是相等的(满足等可能性)；

③不是几何概率，因为区间[－10,10]上的整数只有21个(是有限的)，不满足无限性特征；

④是几何概率，因为在边长为4 cm的正方形和半径为1 cm的圆内均有无数多个点，且这两个区域内的任何一个点都有可能被投到，故满足无限性和等可能性．

2．在区间[1,3]上任取一数，则这个数大于1.5的概率为(　　)

A．0.25   B．0.5

C．0.6   D．0.75

解析：选D.P＝＝0.75.

3．面积为S的△ABC中，D是BC的中点，向△ABC内部投一点，那么点落在△ABD内的概率为(　　)

A.   B.

C.   D.

解析：选A.向△ABC内部投一点的结果有无限个，属于几何概率．设点落在△ABD内为事件M，则P(M)＝＝.

4．(2011年高考江西卷)小波通过做游戏的方式来确定周末活动，他随机地往单位圆内投掷一点，若此点到圆心的距离大于，则周末去看电影；若此点到圆心的距离小于，则去打篮球；否则，在家看书．则小波周末不在家看书的概率为________．

解析：法一：不在家看书的概率＝＝＝.

法二：不在家看书的概率＝1－在家看书的概率＝1－＝.

答案：

一、选择题

1．已知地铁列车每10 min一班，在车站停1 min，则乘客到达站台立即乘上车的概率是(　　)

A.   B.

C.   D.

解析：选C.记“乘客到达站台立即乘上车”为事件A，则A所占时间区域长度为1 min，而整个区域的时间长度为11 min，故由几何概率的概率公式，得P(A)＝.

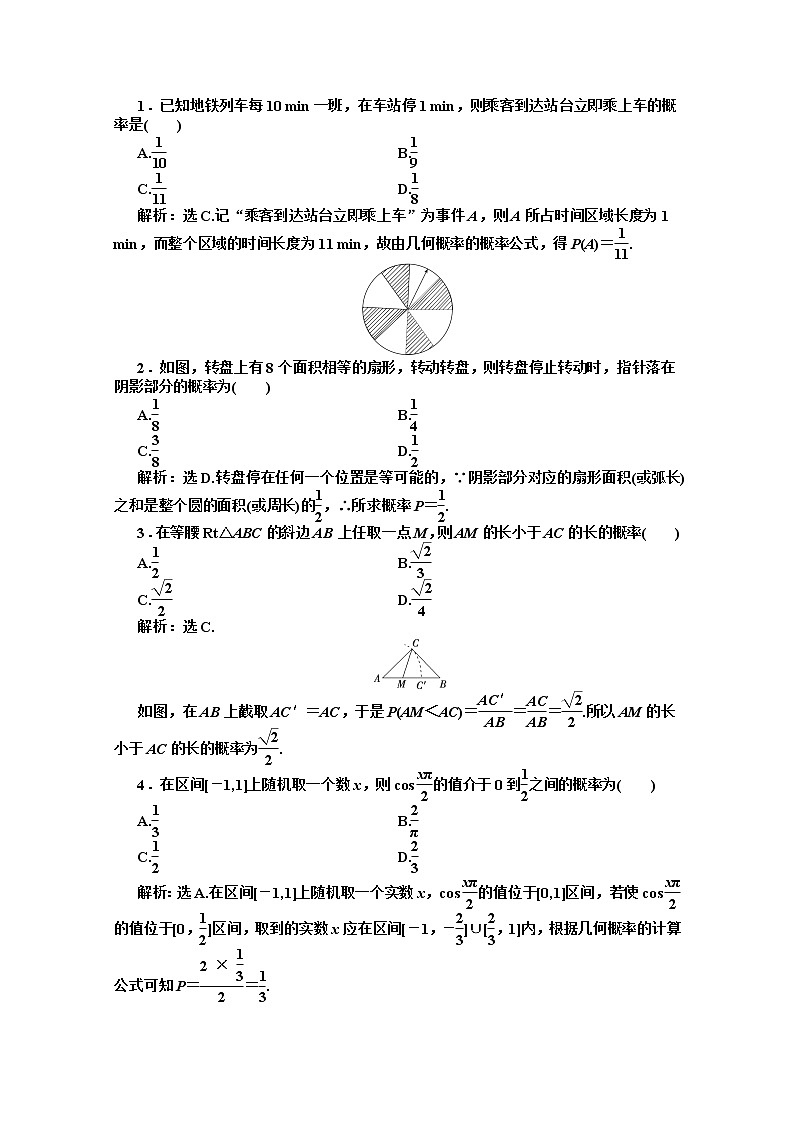
2．如图，转盘上有8个面积相等的扇形，转动转盘，则转盘停止转动时，指针落在阴影部分的概率为(　　)

A.   B.

C.   D.

解析：选D.转盘停在任何一个位置是等可能的，∵阴影部分对应的扇形面积(或弧长)之和是整个圆的面积(或周长)的，∴所求概率P＝.

3．在等腰Rt△ABC的斜边AB上任取一点M，则AM的长小于AC的长的概率(　　)

A.   B.

C.   D.

解析：选C.

如图，在AB上截取AC′＝AC，于是P(AM＜AC)＝＝＝.所以AM的长小于AC的长的概率为.

4．在区间[－1,1]上随机取一个数x，则cos的值介于0到之间的概率为(　　)

A.   B.

C.   D.

解析：选A.在区间[－1,1]上随机取一个实数x，cos的值位于[0,1]区间，若使cos的值位于[0，]区间，取到的实数x应在区间[－1，－]∪[，1]内，根据几何概率的计算公式可知P＝＝.

5．如图，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为，则阴影区域的面积为(　　)

A.   B.

C.   D．无法计算

解析：选B.由几何概率的公式知：＝，

又S正方形＝4，∴S阴影＝.

6．(2011年吉林高一检测)有四个游戏盘，如果撒一粒黄豆落在阴影部分，则可中奖，小明希望中奖，他应当选择的游戏盘为(　　)

解析：选A.根据几何概率的面积比，A中中奖概率为，B游戏盘的中奖概率为，C游戏盘的中奖概率为＝，D游戏盘的中奖概率为＝，故A游戏盘的中奖概率最大．

二、填空题

7．(2010年高考湖南卷)在区间[－1,2]上随机取一个数x，则x∈[0,1]的概率为________．

解析：∵区间[－1,2]的区间长度为3，随机数x的取值区间[0,1]的区间长度为1.

∴由几何概率知x∈[0,1]的概率为.

答案：

8．如图，在一个边长为3 cm的正方形内部有一个边长为2 cm的正方形，向大正方形内随机投点，则所投的点落入小正方形内的概率是________．

解析：由题意知，此题是与面积有关的几何概率．由公式得：P＝＝.

答案：

9．如果函数f(x)＝x2－x－2，x∈[－5,5]，那么任取一点x0，使f(x0)≤0的概率为________．

解析：∵x∈[－5,5]，若f(x)≤0，则：x0－x0－2≤0，

∴－1≤x0≤2，∴P＝＝0.3.

答案：0.3

三、解答题

10.

往如图所示的正方形内随机地投掷飞镖，求飞镖落在阴影部分的概率．

解：由

解得∴|AC|＝.

由解得

∴|BC|＝.

∴Rt△ACB的面积为S△ACB＝××＝.

又∵正方形的面积为4.

∴由几何概率公式得飞镖落在阴影部分的概率为＝.

11．两艘轮船都要停靠同一个泊位，它们可能在一昼夜的任意时刻到达，设甲、乙两艘轮船停靠泊位的时间分别是2小时与4小时，求有一艘轮船停靠泊位时必须等待一段时间的概率．

解：

如图所示，以x和y分别表示甲、乙两船到达泊位的时间，则有一艘船停靠泊位时必须等待一段时间的等价条件是2≤x－y≤4，在平面直角坐标系内，(x，y)的所有可能结果是边长为24的正方形，而事件A“有一艘船停靠泊位时必须等待一段时间”的所有可能结果由图中的阴影部分来表示，

μA＝242－×222－×202＝134，

μΩ＝242＝576，

所以P(A)＝＝＝.

故有一艘轮船停靠泊位时必须等待一段时间的概率为.

12．如图，圆O方程为x2＋y2＝4.

(1)已知点A的坐标为(2,0)，B为圆周上任意一点，求弧长小于π的概率；

(2)若P(x，y)为圆O内任意一点，求点P到原点距离大于1的概率．

解：(1)记事件M为“弧长小于π”，

∵圆O的周长C＝4π，满足事件M的弧长l＝2π，

∴弧长小于π的概率P(M)＝＝.

(2)记事件N为“点P到原点距离大于1”，则事件N构成的区域是圆x2＋y2＝1与圆x2＋y2＝4所构成的圆环，其面积为4π－π＝3π，而圆O的面积为4π，

所以点P到原点距离大于1的概率P(N)＝＝.