苏教版必修53.3.1 二元一次不等式表示的平面区域练习

这是一份苏教版必修53.3.1 二元一次不等式表示的平面区域练习，共5页。试卷主要包含了了解线性规划问题的图解法，课堂小结，课后作业等内容，欢迎下载使用。
1．解线性约束条件、线性目标函数、线性规划概念；
2．在线性约束条件下求线性目标函数的最优解；
3．了解线性规划问题的图解法。
教学重点：线性规划问题。
教学难点：线性规划在实际中的应用。
教学过程：
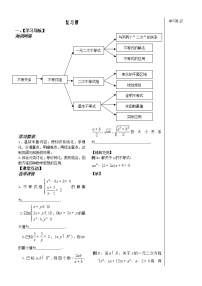
1．复习回顾：
上一节，我们学习了二元一次不等式表示的平面区域，这一节，我们将应用这一知识来解决线性规划问题．所以，我们来简要回顾一下上一节知识．（略）
2．讲授新课：
例1：设z＝2x＋y，式中变量满足下列条件：
eq \b\lc\{(\a\al(x－4y≤－3,3x＋5y≤25,x≥1)) ，求z的最大值和最小值.
解：变量x，y所满足的每个不等式都表示一个平面
区域，不等式组则表示这些平面区域的公共
区域．（如右图）．
作一组与l0：2x＋y＝0平行的直线l： 2x＋y＝t.t∈Ｒ可知：当l在l0的右上方时，直线l上的点（x，y）满足2x＋y＞0，即t＞0，而且，直线l往右平移时，t随之增大，在经过不等式组①所表示的公共区域内的点且平行于l的直线中，以经过点A（５，２）的直线l2所对应的t最大，以经过点B（１，１）的直线l1所对应的t最小．所以
zmax＝2×5＋2＝12 zmin＝2×1＋1＝3
说明：例1目的在于给出下列线性规划的基本概念．
线性规划的有关概念：
①线性约束条件：
在上述问题中，不等式组是一组变量x、y的约束条件，这组约束条件都是关于x、y的一次不等式，故又称线性约束条件．
②线性目标函数：
关于x、y的一次式z＝2x＋y是欲达到最大值或最小值所涉及的变量x、y的解析式，叫线性目标函数．
③线性规划问题：
一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题．
④可行解、可行域和最优解：
满足线性约束条件的解（x，y）叫可行解．
由所有可行解组成的集合叫做可行域．
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解．
Ex：P841，2，3
例2：在x≥0，y≥0，3x＋y≤3及2x＋3y≤6的条件下，试求x－y的最值。
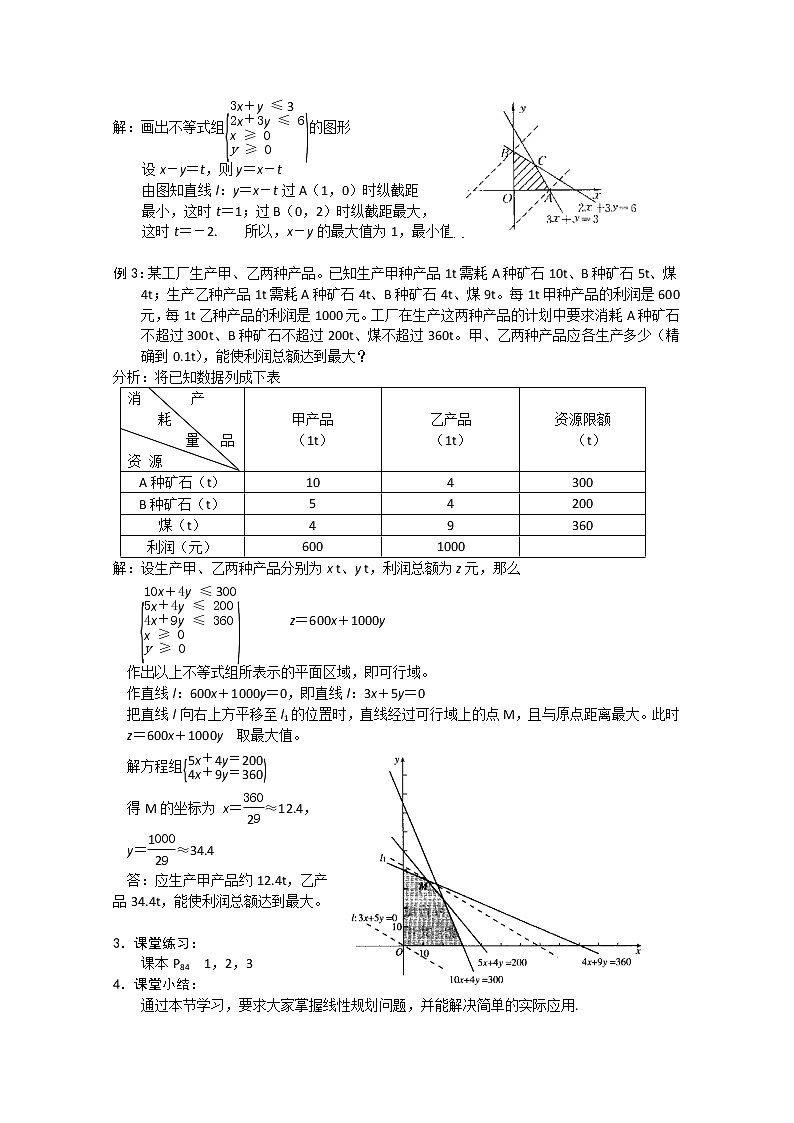
解：画出不等式组 eq \b\lc\{(\a\al(3x＋y≤3,2x＋3y≤6,x≥0,y≥0)) 的图形
设x－y＝t，则y＝x－t
由图知直线l：y＝x－t过A（1，0）时纵截距
最小，这时t＝1；过B（0，2）时纵截距最大，
这时t＝－2. 所以，x－y的最大值为1，最小值为－2。
例3：某工厂生产甲、乙两种产品。已知生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t；生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t。每1t甲种产品的利润是600元，每1t乙种产品的利润是1000元。工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t。甲、乙两种产品应各生产多少（精确到0.1t），能使利润总额达到最大？
分析：将已知数据列成下表
解：设生产甲、乙两种产品分别为x t、y t，利润总额为z元，那么
eq \b\lc\{(\a\al(10x＋4y≤300,5x＋4y≤200,4x＋9y≤360,x≥0,y≥0)) z＝600x＋1000y
作出以上不等式组所表示的平面区域，即可行域。
作直线l：600x＋1000y＝0，即直线l：3x＋5y＝0
把直线l向右上方平移至l1的位置时，直线经过可行域上的点M，且与原点距离最大。此时 z＝600x＋1000y 取最大值。
解方程组 eq \b\lc\{(\a\al(5x＋4y＝200,4x＋9y＝360))
得M的坐标为 x＝ eq \f(360,29) ≈12.4，
y＝ eq \f(1000,29) ≈34.4
答：应生产甲产品约12.4t，乙产
品34.4t，能使利润总额达到最大。
3．课堂练习：
课本P84 1，2，3
4．课堂小结：
通过本节学习，要求大家掌握线性规划问题，并能解决简单的实际应用.
5．课后作业：
课本P87习题 3，4

教学后记：

线性规划
例1：某工厂生产甲、乙两种产品。已知生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t；生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t。每1t甲种产品的利润是600元，每1t乙种产品的利润是1000元。工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t。甲、乙两种产品应各生产多少（精确到0.1t），能使利润总额达到最大？
例2：某工厂有甲、乙两种产品，按计划每天各生产不少于15t，已知生产甲产品1t需煤9t，电力4kw，劳动力3个（按工作日计算）；生产乙产品l t需煤4t，电力5kw，劳动力10个；甲产品每吨价7万元，乙产品每吨价12万元；但每天用煤量不得超过300吨，电力不得超过200 kw，劳动力只有300个，问每天各生产甲、乙两种产品多少吨，才能既保证完成生产任务，又能为国家创造最多的财富。
例3：一位农民有田2亩，根据他的经验：若种水稻，则每亩每期产量为400 kg；若种花生，则每亩每期产量为100 kg，但水稻成本较高，每亩每期需240元，而花生只要80元，且花生每 kg可卖5元，稻米每kg只卖3元，现在他只能凑足400元，问这位农民对两种作物各种多少亩，才能得到最大利润？
例3：要将两种大小不同的钢板截成Ａ、Ｂ、Ｃ三种规格，每张钢板可同时截得三种规格的小钢板的块数如下表所示：
今需要A、B、C三种规格的成品分别为15、18、27块，问各截这两种钢板多少张可得所需三种规格成品，且使所用钢板张数最少？
消 产
耗 量 品
资 源
甲产品
（1t）
乙产品
（1t）
资源限额
（t）
A种矿石（t）
10
4
300
B种矿石（t）
5
4
200
煤（t）
4
9
360
利润（元）
600
1000
规格类型
钢板类型
Ａ规格
Ｂ规格
Ｃ规格
第一种钢板
２
１
１
第二种钢板
１
２
３