数学高中三年级 第一学期14.2空间直线与直线的位置关系图文课件ppt

这是一份数学高中三年级 第一学期14.2空间直线与直线的位置关系图文课件ppt，共19页。PPT课件主要包含了复习巩固，直线在平面上的射影，B1C，三垂线定理，三垂线定理及其逆定理，练习和作业等内容，欢迎下载使用。
1、直线和平面垂直的判定定理为 2、①过平面外一点向这个平面引垂线，垂足叫做这个点在 这个平面内的 。 ②一条直线和一个平面相交，但不和这个平面垂直，那么这条直线叫做这个平面的 。 ③从斜线上斜足以外的一点向平面引垂线，经过垂足和斜足的直线叫 。
如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面
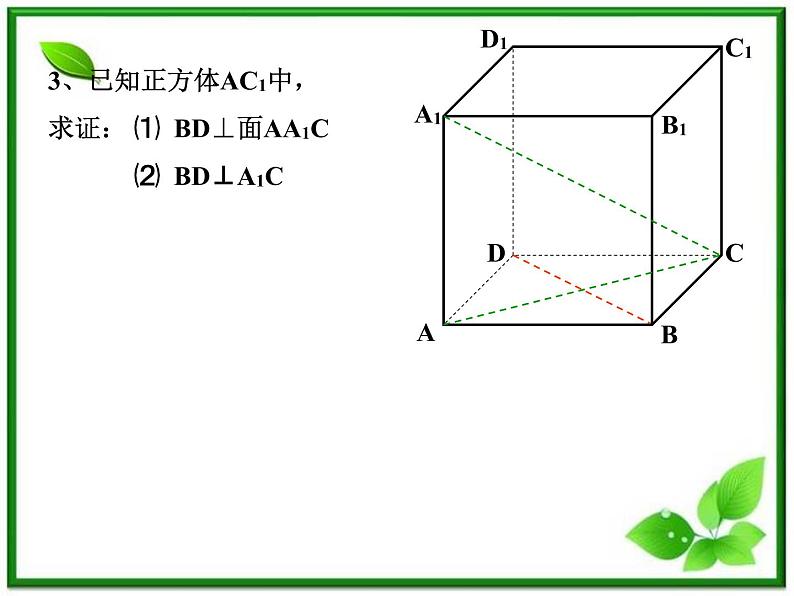
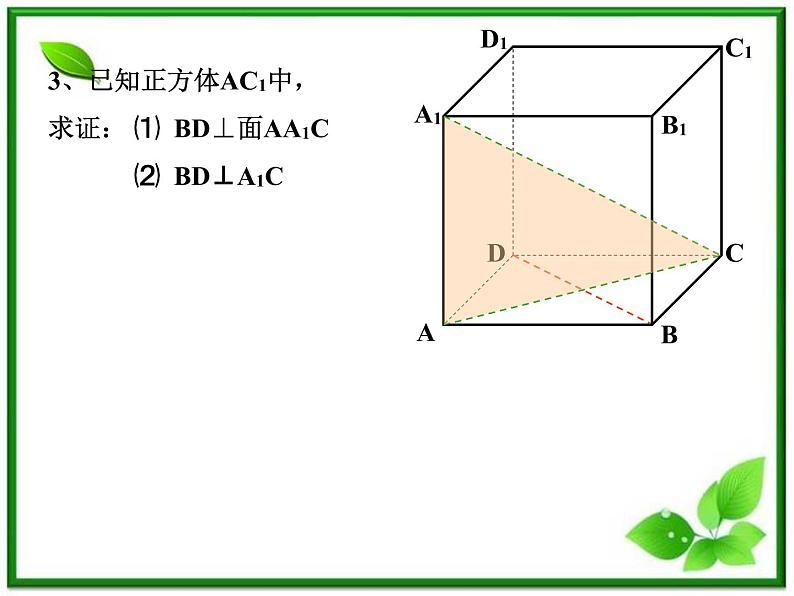
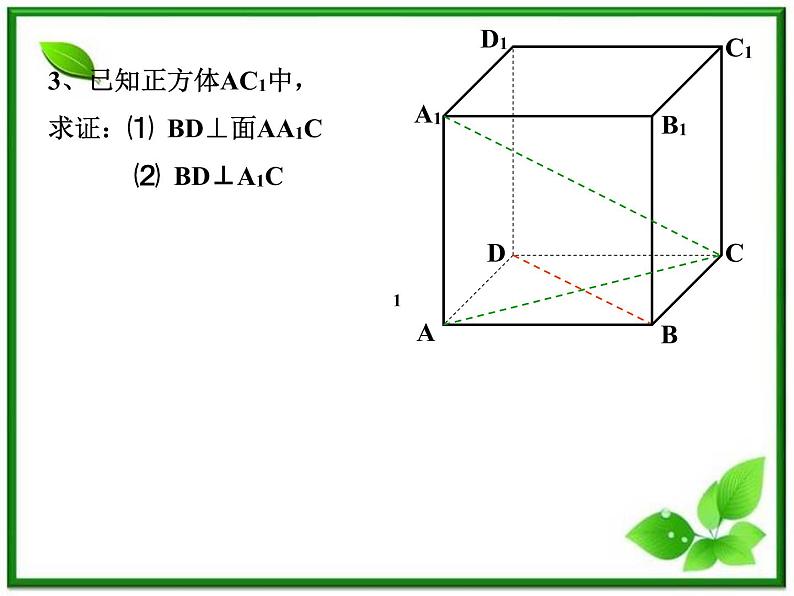
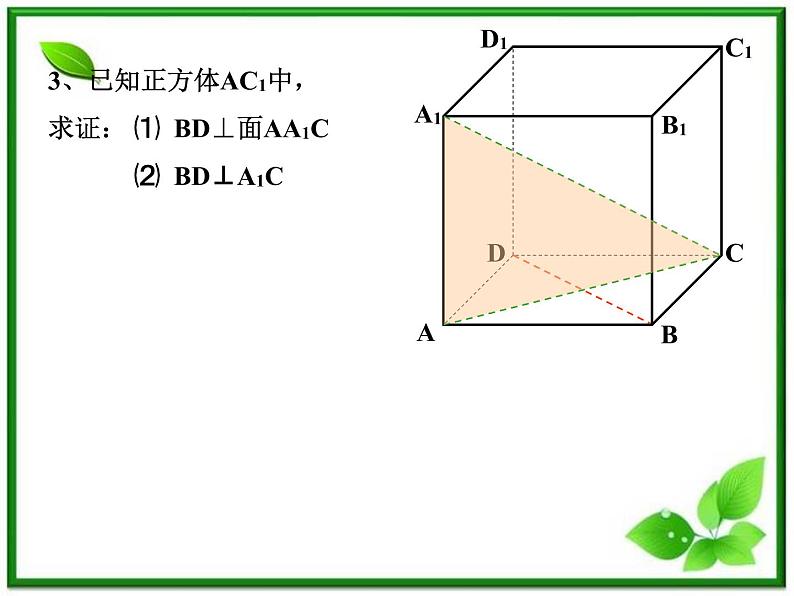
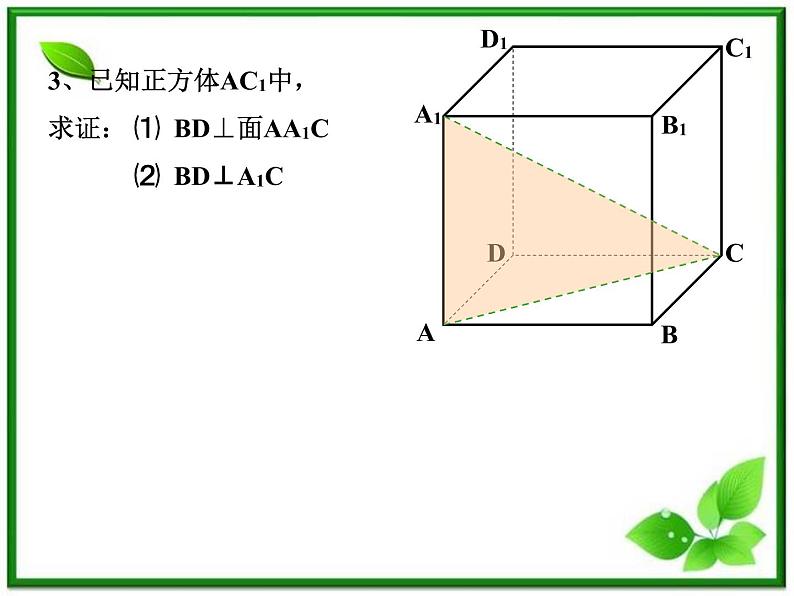
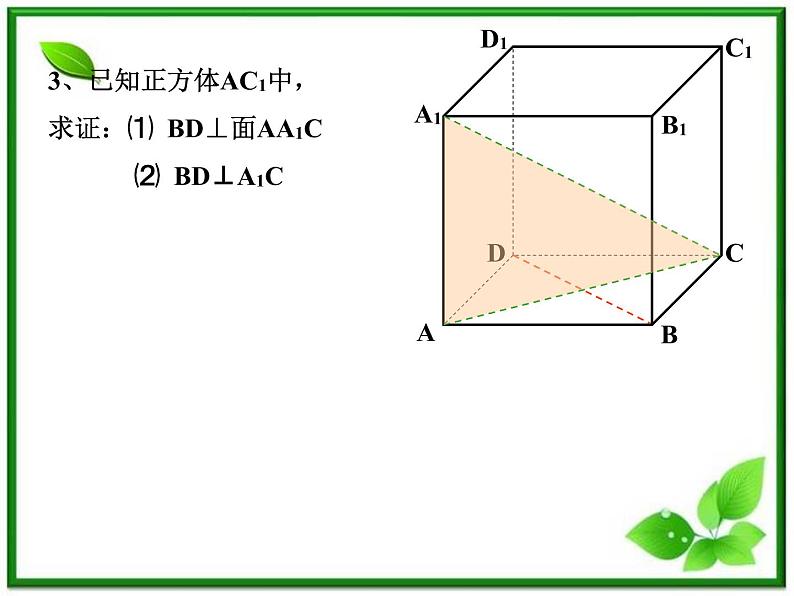
3、已知正方体AC1中，求证： ⑴ BD⊥面AA1C ⑵ BD⊥A1C
3、已知正方体AC1中，求证：⑴ BD⊥面AA1C ⑵ BD⊥A1C
证明：证明：⑴在正方体AC1中，AA1⊥面ABCD ∴AA1⊥BD又BD⊥AC AC∩AA1=A∴BD ⊥面AA1C ⑵ 由⑴知BD ⊥面AA1C A1C在面AA1C ∴BD⊥A1C
4、在正方体AC1中，AC1在平面ABCD、BB1C1C内的射影分别（ ） 平面 ABCD、BB1C1C内 的 直线BD、BC1分别 与 对应的斜线是否垂直？与对应的射影呢？
在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。
已知：PO、PA分别是平面α的 垂线、斜线， OA是 PA在平面α内的射影，且a在平面α 内， a ⊥ OA求证： a ⊥PA
证明：∵PO⊥平面α 垂 且a在平面α内∴PO ⊥ a 又a⊥ OA OA ∩ PO=O ∴a⊥面 PAO ∴a ⊥PA
关键：⑴ 寻找“垂面” ⑵ 确定“射影” ⑶判别“垂直”
三线：斜线、射影、面内一条直线
在平面内的一条直线、如果它和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直。
已知：如 图，正方体AC1中，E、F分别为棱AB、BC的中点求证：C1E⊥DF
证明：正方形ABCD 中，E、F分别为AB、BC中点，∴△DCF≌△CBE. ∠CDF＝ ∠BCE 又∠CDF＋ ∠DFC＝900 ∴ ∠BCE＋ ∠DFC＝900 ∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。　由三垂线定理知 C1E ⊥DF
1、已知：O为正方体AC1的底面ABCD的中点。求证：D1O⊥EF2、已知P为△ABC所在平面外一点， 若P在平面ABC 内的射影是△ABC的垂心。求证：PA⊥BC PB⊥AC PC⊥AB3、如图，PO是平面α 的斜线，O为斜足，PA⊥α于A，OC在平面 α内ABDC于B若PO与平面 α 成300角 ，∠AOB=450。PA=2cm求： ⑴PB的长⑵∠POB的大小