






数学沪教版15.5几何体的体积教案配套课件ppt
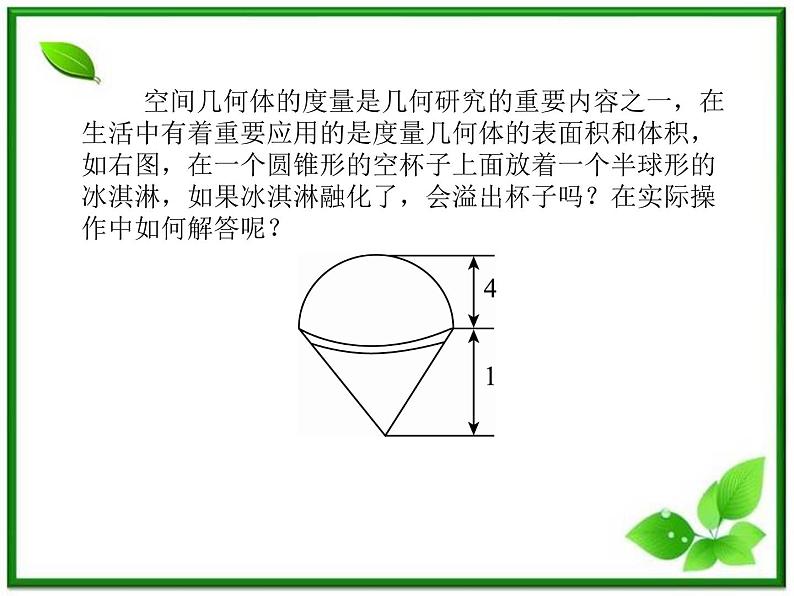
展开空间几何体的度量是几何研究的重要内容之一,在生活中有着重要应用的是度量几何体的表面积和体积,如右图,在一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?在实际操作中如何解答呢?
1.几何体的体积是几何体占有空间部分的大小,其主要性质有:①完全相同的几何体的体积________;②体积相等的几何体叫________;③两个等积体的几何体的形状________相同;④底面积相等、高相等的两个柱体(或锥体)体积________.2.①棱柱的体积公式:V柱体=_______(S为底面面积,h为柱体的高);②棱锥的体积公式:V锥体=_________(S为底面面积,h为棱锥的高);③台体的体积公式:V台体=________(S′、S为两底面面积,h为台体的高).
3.①圆柱的体积公式:V柱体=________(R为底面圆的半径,h为圆柱的高);②圆锥的体积公式:V圆锥体=________(R为底面圆的半径,h为圆锥的高);③圆台体的体积公式:V圆台体=______(r、R为两底面圆半径,h为台体的高).4.球的体积公式:V球=____(R为球半径),表面积公式为:S球=______.
棱、锥、台和球的体积公式
祖暅原理:“幂势既同,则积不容异”是推出以上公式的基础,由此我们不难概括出多面体和旋转体的体积性质:①完全相同的几何体的体积相等;②体积相等的几何体叫等积体;③两个等积体的几何体的形状不一定相同;④底面积相等、高相等的两个柱体(或锥体)体积相等,等积转化是今后求相关几何体的体积的重要策略.对于柱、锥、台的体积公式可以从它们间的转化关系上加强记忆:
对于球体的体积公式可以类比锥体的体积公式形象地记忆为 (4πR2)·R.
棱柱ABC-A′B′C′的侧面AA′C′C的面积为S,且这侧面与它相对的侧棱BB′之间的距离为a,求这棱柱的体积.
分析:此题若直接求底ABC的面积及其上的高,将是困难的,能否考虑采取补充或截割的办法,以已知面积的侧面为底来解呢?如右图设法补上一个与原三棱柱全等的三棱柱,成为一个平行六面体,再将面AA′C′C看作底求出.
解析:如右图过侧棱BB′、CC′分别作侧面AC′、AB′的平行平面,DD′是交线;再伸展两底面,得到平行六面体ABDC-A′B′D′C′.∵侧面AA′C′C的面积为S,设此面为底面,则平行六面体BDD′B-ACC′A′的高为a.
规律总结:这里几何体虽然是柱体,但在已知条件下不易求体积,此解法中将三棱柱补成平行六面体后便于求体积,要认真领会.
如右图所示,三棱锥的顶点为P,PA、PB、PC为三条侧棱,且PA、PB、PC两两互相垂直,又PA=2,PB=3,PC=4,求三棱锥P-ABC的体积V.
规律总结:锥体的高实质上是与锥体底面垂直的线段,由前面知识可知,只要一条直线与一个平面的两条相交直线垂直,则它就与这个平面垂直.本例中,由于PA⊥PB且PA⊥PC,而PB与PC相交于点P,所以PA垂直平面PBC,即PA为三棱锥A-PBC的高,从而顺利地求出其体积.本例中,不是先求出以ABC为底面的三棱锥的高,而是把它转化为三棱锥A-PBC的高,这种方法的依据是:三棱锥又称为四面体,它的每一个面都可当做底面来处理.这一方法叫做体积转移法(或称等积法),随着知识的增多,它的应用越来越广,因此必须熟练掌握.
1.已知三角形ABC的边长分别是AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得几何体的体积.
三棱台ABC-A1B1C1中,AB:A1B1=1:2,则三棱锥A1-ABC,B-A1B1C,C-A1B1C1的体积之比为________.
解析:如右图,三棱锥A1-ABC的顶点看做A1,底面看做ABC;三棱锥C-A1B1C1的顶点看做C,底面看做A1B1C1;三棱锥B-A1B1C可看做棱台减去两个三棱锥A1-ABC和C-A1B1C1后剩余的几何体,分别求几何体的体积,然后相比即可.
规律总结:(1)求台体体积的常用方法有三:一是利用台体的体积公式来求解,这就需要知道台体的上、下底面积和高;二是抓住台体是由锥体截割而来的这一特征,把它还原成锥体,利用锥体体积公式来求其台体的体积;三是利用割补法来求其体积.(如本例)(2)三棱柱、三棱台可以分割成三个三棱锥,分割后可由锥体的体积求柱体和台体的体积,在立体几何中,割补法是重要的思想方法.
2.已知一正四棱台的上底边长为4 cm,下底边长为8 cm,高为3 cm,求其体积.
三个球的半径之比是1:2:3,求证:最大球的体积等于其他两个球体积和的三倍.
分析:由三个球的半径之比为1:2:3,可设三个球半径分别为r、2r和3r,则三个球的体积都可以表示成r的代数式,然后再研究它们体积的数量关系.
规律总结:解决球的体积问题,首先要熟练掌握球的体积公式,它可以想象成以球的半径为半径,球的直径为高的圆柱的体积的三分之二.在求球的体积时,其关键是求球的半径.
3.一平面截一球得直径是6 cm的圆面,球心到这个平面的距离是4 cm,则该球的体积是________.
已知球的两平行截面的面积为5π和8π,它们位于球心的同一侧,且相距为1,求这个球的表面积.
分析:要求球的表面积,只需求出球的半径,因此要抓住球的轴截面(过球的直径的球的平面).解析:如图所示,设以r1为半径的截面面积为5π,以r2为半径的截面面积为8π,O1O2=1,球的半径为R,OO2=x,那么可得下列关系式:
规律总结:球的轴截面(球的过直径的截面)是将球的问题(立体问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.
4.用两个平行平面去截半径为R的球面,两个截面圆半径为r1=24 cm,r2=15 cm,两截面间的距离为d=27 cm,求球的表面积.
解析:显然,两平行平面所截得的两截面圆应在球心的异侧,设垂直于截面的大圆面交两截面圆于A1B1、A2B2,上述大圆垂直于A1B1的直径交A1B1、A2B2于O1、O2,如下图所示.
有关组合体的表面积和体积
求体积为V的正方体的外接球的表面积和体积.
分析:如右图所示,显然正方体的中心为其外接球的球心,过球心作平行于正方体任一面的截面,则其截面为圆内一正方形(正方形的各顶点均在内,而不是在圆上).因此这样的截面无法反映球的半径与正方体的棱长的关系.注意到球心必在正方体的一个对角面上,因此,以正方体的一个对角面作截面即可.
解析:如上图,过正方体的对角面ACC1A1作球的截面,则球心为AC1的中点,设正方体的棱长为x,则
规律总结:正方体外接球的轴截面不是圆内一正方形,而是圆内一矩形,因此在解决棱柱内切球和外接球的有关问题,必须谨慎地作其轴截面,切忌想当然地作图,平时学习时最好是自己动手做实物模型,由模型作出相应的轴截面即可.
5.如右图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF= ,EF与面AC的距离为2,求该多面体的体积.
分析:这个多面体是一个不规则的图形,其形状犹如木工常用的木楔,立体几何中把这种几何体称为楔体,所以必须运用割补的方法,将其化归为棱柱或棱锥进行体积计算.
方法点拨:(1)本题充分结合图形的特征,强化割补的思想方法,考查多面体体积的计算以及空间想象能力和运算能力.(2)某些立体几何问题,如果直接根据原有的图形解题困难时,那么不妨将此图形巧妙地分割或补形,转化为我们熟悉的柱、锥等比较规则的或易于研究的几何体来处理,从而实现化繁为简、化难为易,便于解决问题.(3)等积转化,亦称等积变换,通常是指用不同的方式求同一几何体的体积(或同一平面图形的面积).
棱柱、棱锥和棱台的体积
2.已知高为3的直棱柱ABC-A1B1C1的底面是边长为1的正三角形(如右图所示),则三棱锥B1-ABC的体积为________.
10.在三棱锥A-BCD中,P、Q分别在棱AC、BD上,连接AQ、CQ、BP、PQ,若三棱锥A-BPQ、B-CPQ、C-DPQ的体积分别为6、2、8,则三棱锥A-BCD的体积为________.
解析:如右图,VA-BPQ:VB-CPQ=6:2,VB-APQ:VB-CPQ=S△APQ :S△CPQ=6:2,类似地VA-DPQ:VC-DPQ=VD-APQ:VD-CPQ=S△APQ:S△CPQ=6:2.其中VC-DPQ=8.∴VA-DPQ:8=6:2,∴VA-DPQ=24,∴VA-BDC=6+2+8+24=40.答案:40
人教版新课标A选修4-1五 与圆有关的比例线段课文课件ppt: 这是一份人教版新课标A选修4-1五 与圆有关的比例线段课文课件ppt,共32页。PPT课件主要包含了第3题图,第4题图等内容,欢迎下载使用。
数学选修4-1四 弦切角的性质教学演示ppt课件: 这是一份数学选修4-1四 弦切角的性质教学演示ppt课件,共32页。
2021学年一 圆周角定理教课内容ppt课件: 这是一份2021学年一 圆周角定理教课内容ppt课件,共30页。PPT课件主要包含了解析如图所示等内容,欢迎下载使用。













