高中数学苏教版必修13.1.2 指数函数教案

这是一份高中数学苏教版必修13.1.2 指数函数教案，共3页。教案主要包含了知识归纳，针对训练等内容，欢迎下载使用。
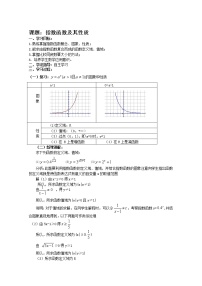
2．1．2指数函数（2）教学目标：1．掌握指数函数的图象和性质；2．能运用指数函数的图象和性质解决一些实际问题。3．培养从特殊到一般的抽象、概括、归纳能力。重点、难点：能运用指数函数的图象和性质解决一些实际问题一、知识归纳1．设，则它们的大小关系为                。2．若函数的图象经过第二、三、四象限，则一定有（    ）①    ② a>1，且b>0③    ④ a>1，且b<03．已知实数a，b满足等式，下列五个关系式①0<b<a；②a<b<0；③0< a < b；④b < a <0；⑤a=b=0。其中不可能成立的关系式有                         。4．若直线与函数的图象有两个公共点，则a的取值范围是                。5．函数的值域是             。6．当x>0时，函数的值总大于1，则实数a的取值范围是       。 二、例题选讲学点一：与指数函数相关的定义域、值域。例1．求下列函数的定义域与值域（1）； （2）      学点二：与指数函数相关的函数的单调性例2．讨论函数的单调性并求值域。      学点三：指函数的应用问题例3．某林区1999年木材蓄积量200万m3，由于采取了封山育林、严禁采伐等措施，使木材蓄积量的年平均递增率能达到5%。（1）若经过x年后，该林区的木材蓄积量为y万m3，求的表达式，并求此函数的定义域；（2）作出函数的图象，并应用图象求经过多少年后，林区的木材蓄积量能达到300万m3？     学点四：与指函数函数有关的奇偶性例4．已知函数是奇函数，求实数a的值。            三、针对训练1．某人2002年7月1日到银行存入一年期款a元，若按年利率x复利计算，则到2005年7月1日可取回           元。2．函数在[0，1]上最大值与最小值的和为3，则a=             。3．函数的单调增区间为             。4．已知（1）证明：是奇函数；（2）证明：在定义域内是增函数；（3）求的值域。     5．求函数的最大值和最小值。