
高中苏教版3.1.2 指数函数教学设计
展开2012高一数学 指数函数(3)学案
学习目标:
1. 理解指数函数的定义,初步掌握指数函数的图象,性质及其简单应用.
2. 通过指数函数的图象和性质的学习,培养学生观察,分析,归纳的能力,进一步体会数形结合的思想方法.
3. 通过对指数函数的研究,使学生能把握函数研究的基本方法,激发学生的学习兴趣.
课前预复习:
引例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是什么?
引例2:某种商品的价格从今年起每年降低15%,设原来的价格为1,x年后的价格为y,则y与x的函数关系式为
在,中指数x是自变量,底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个大于0且不等于1的常量的函数叫做指数函数.
问题解决:
1.指数函数的定义:函数叫做指数函数,其中x是自变量,函数定义域是R
探究1:为什么要规定a>0,且a1呢?
探究2:函数是指数函数吗?
2.指数函数的图象和性质:
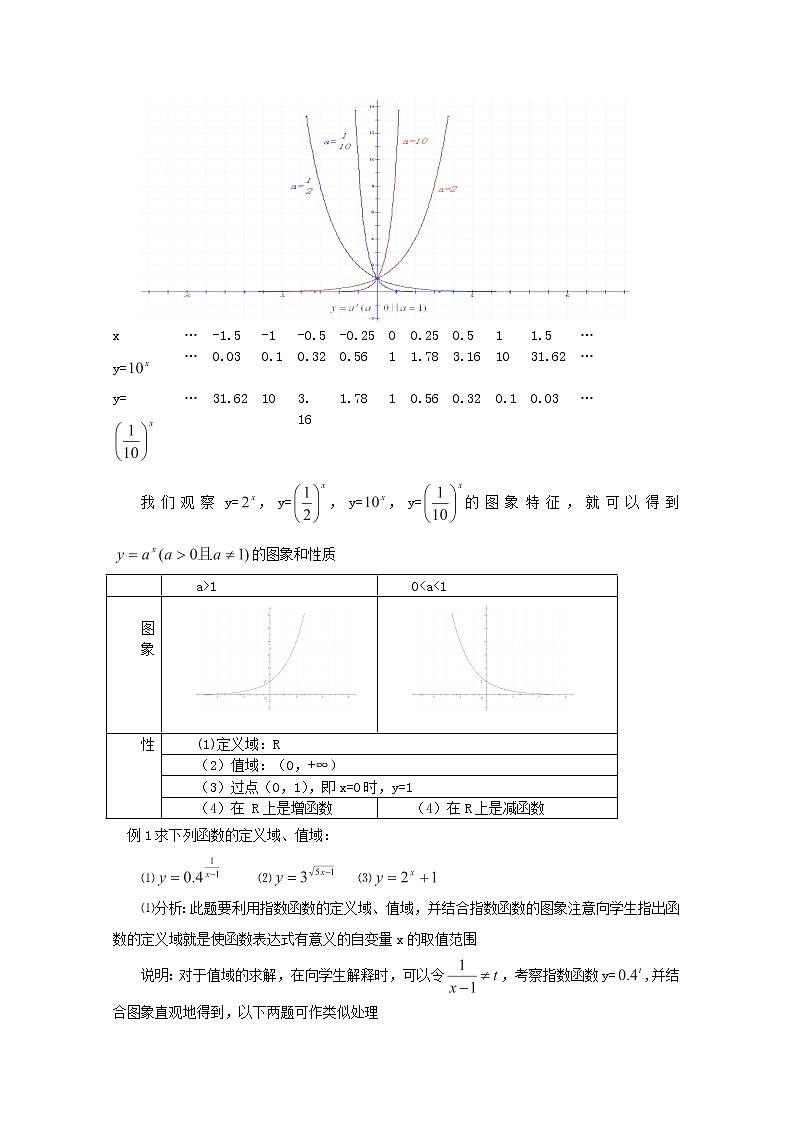
在同一坐标系中分别作出函数y=,y=,y=,y=的图象.
x | … | -3 | -2 | -1 | -0.5 | 0 | 0.5 | 1 | 2 | 3 | … |
y= | … | 0.13 | 0.25 | 0.5 | 0.71 | 1 | 1.4 | 2 | 4 | 8 | … |
y= | … | 8 | 4 | 2 | 1. 4 | 1 | 0.71 | 0. 5 | 0.25 | 0.13 | … |
x | … | -1.5 | -1 | -0.5 | -0.25 | 0 | 0.25 | 0.5 | 1 | 1.5 | … |
y= | … | 0.03 | 0.1 | 0.32 | 0.56 | 1 | 1.78 | 3.16 | 10 | 31.62 | … |
y= | … | 31.62 | 10 | 3. 16 | 1.78 | 1 | 0.56 | 0.32 | 0.1 | 0.03 | … |
我们观察y=,y=,y=,y=的图象特征,就可以得到的图象和性质
| a>1 | 0<a<1 |
图 象 | ||
性 | (1)定义域:R | |
(2)值域:(0,+∞) | ||
(3)过点(0,1),即x=0时,y=1 | ||
(4)在 R上是增函数 | (4)在R上是减函数 | |
例1求下列函数的定义域、值域:
⑴ ⑵ ⑶
⑴分析:此题要利用指数函数的定义域、值域,并结合指数函数的图象注意向学生指出函数的定义域就是使函数表达式有意义的自变量x的取值范围
说明:对于值域的求解,在向学生解释时,可以令,考察指数函数y=,并结合图象直观地得到,以下两题可作类似处理
通过此例题的训练,学会利用指数函数的定义域、值域去求解指数形式的复合函数的定义域、值域,还应注意书写步骤与格式的规范性
练习反馈:
求下列函数的定义域和值域:
⑴ ⑵
例2已知指数函数 (a>0,且a≠1)的图象经过点(3,π),求
f(0)、f(1)、f(-3)的值.
例3:比较下列各题中两个值的大小:
①,; ②,; ③,
小结:对同底数幂大小的比较用的是指数函数的单调性,必须要明确所给的两个值是哪个指数函数的两个函数值;对不同底数是幂的大小的比较可以与中间值进行比较.
练习反馈:
⑴比较大小: ,
⑵已知下列不等式,试比较m、n的大小:
m < n;m < n.
⑶比较下列各数的大小: ,
课堂小结 : 本节课学习了以下内容:指数函数概念,指数函数的图象和性质
课后巩固
基础训练:
- 函数是指数函数,则a的值为
- 已知,则函数的图像不经过第 象限
- 根据条件写出正数a的取值范围
(2)
- 函数的图像横过定点
- 求下列函数的定义域和值域
(1)
能力提升:
- 若集合
- 若函数在R上递减,则a的取值范围
- 函数在上的最大值和最小值的和为3,则a等于
- 函数和的图像关于 对称
- 将函数的图像向右平移2个单位,再向下平移1个单位,则所得函数的解析式
- 函数的解集
- 已知函数
(1)作出其图像
(2)由图像指出函数的单调区间
(3)由图像指出当x取何值时,函数有最值
- 已知函数在区间上的最大值为14,求a的值
高中数学苏教版必修13.2.2 对数函数教学设计及反思: 这是一份高中数学苏教版必修13.2.2 对数函数教学设计及反思,共4页。教案主要包含了学习目标,课前预复习,问题解决,练习反馈,要点归纳与方法小结,巩固练习等内容,欢迎下载使用。
高中数学苏教版必修13.2.2 对数函数教案: 这是一份高中数学苏教版必修13.2.2 对数函数教案,共2页。教案主要包含了情境问题,学生活动,数学运用等内容,欢迎下载使用。
2021学年3.1.2 指数函数教案: 这是一份2021学年3.1.2 指数函数教案,共4页。教案主要包含了填空题,解答题等内容,欢迎下载使用。













