苏教版必修13.2.2 对数函数教案设计

这是一份苏教版必修13.2.2 对数函数教案设计，共7页。教案主要包含了学习导航，互动探究，迁移应用等内容，欢迎下载使用。
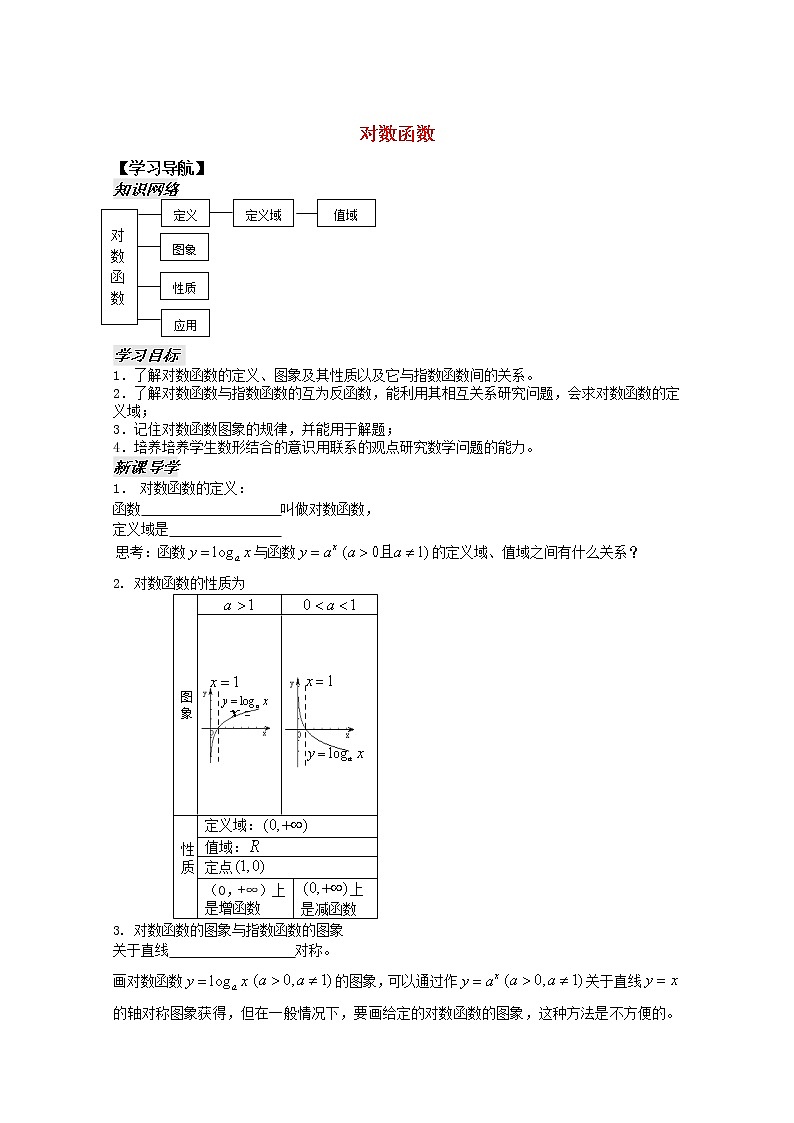
对数函数 【学习导航】 知识网络        学习目标 1．了解对数函数的定义、图象及其性质以及它与指数函数间的关系。2．了解对数函数与指数函数的互为反函数，能利用其相互关系研究问题，会求对数函数的定义域；3．记住对数函数图象的规律，并能用于解题；4．培养培养学生数形结合的意识用联系的观点研究数学问题的能力。新课导学1．   对数函数的定义：函数                    叫做对数函数，定义域是                思考：函数与函数的定义域、值域之间有什么关系？2. 对数函数的性质为图象            性质 定义域：值域：定点（0，+∞）上是增函数上是减函数3. 对数函数的图象与指数函数的图象关于直线                  对称。画对数函数的图象，可以通过作关于直线的轴对称图象获得，但在一般情况下，要画给定的对数函数的图象，这种方法是不方便的。所以仍然要掌握用描点法画图的方法，注意抓住特殊点（1，0）及图象的相对位置。4.指数函数定义域和值域分别是对数函数的               。【互动探究】例1：求下列函数的定义域（1）；             （2） ；   （3）      （4）[分析]：此题主要利用对数函数的定义域求解。               例2：利用对数函数的性质，比较下列各组数中两个数的大小：（1），；　（2），；（3），；    （4），，点评: 本例是利用对数函数的增减性比较两个对数的大小，当不能直接进行比较时，可在两个对数中间插入一个已知数（如1 或0），间接比较上述两个对数的大小。             例3说明函数与函数图像的关系。        例4画出函数的图像，并根据图像写出函数的单调区间。        【迁移应用】1.求函数的定义域，并画出函数的图象。     2. 比较下列各组数中两个值的大小：（1），； （2），；（3），.（4），，       3.解下列方程：（1）  （2）（3）（4）      4．解不等式：（1）（2） 答案2．    对数函数的定义：函数 叫做对数函数(logarithmic function),定义域是 思考：函数与函数的定义域、值域之间有什么关系？2. 对数函数的性质为图象            性质（1）定义域：（2）值域：（3）过点，即当时，（4）在（0，+∞）上是增函数（4）在上是减函数3. 对数函数的图象与指数函数的图象关于直线对称。画对数函数的图象，可以通过作关于直线的轴对称图象获得，但在一般情况下，要画给定的对数函数的图象，这种方法是不方便的。所以仍然要掌握用描点法画图的方法，注意抓住特殊点（1，0）及图象的相对位置。4.指数函数与对数函数称为互为反函数。指数函数的定义域和值域分别是对数函数的值域和定义域。5．一般地，如果函数存在反函数，那么它的反函数，记作思考：互为反函数的两个函数的定义域和值域有什么关系？原函数的定义域和值域分别是反函数的值域和定义域。例1：求下列函数的定义域（1）；             （2） ；   （3）       （4）[分析]：此题主要利用对数函数的定义域求解。（1）由得，∴函数的定义域是；（2）由得，∴函数 的定义域是 （3）得或∴函数的定义域是 （4）由  得∴，函数的定义域是例2：利用对数函数的性质，比较下列各组数中两个数的大小：（1），；　（2），；（3），；     （4），，【解】（1）对数函数在上是增函数，于是；（2）对数函数在上是减函数，于是；（3）．∵，  ，；（4）∵，而∴（1）点评: 本例是利用对数函数的增减性比较两个对数的大小，当不能直接进行比较时，可在两个对数中间插入一个已知数（如1 或0），间接比较上述两个对数的大小。例3若且，求的取值范围    （2）已知，求的取值范围；【解】（1）当时在上是单调增函数，当时在上是单调减函数，综上所述：的取值范围为（2）当，即时由，  解得： ∴当，即时由， 解得： ，此时无解。综上所述：的取值范围为点评:本题的关键是利用对数函数的单调性解不等式，一定要注意对数函数定义域。1.求函数的定义域，并画出函数的图象。2. 比较下列各组数中两个值的大小：（1），； （2），；（3），.（4），，3.解下列方程：（1）  （2）（3）（4）4．解不等式：（1）（2）答案：1．略  2．（1）（2）（3）当时，，      当时， （4）3．（1） （2）（3） （4）4．（1）  （2）