人教版新课标B必修21.2.3空间中的垂直关系图文课件ppt

这是一份人教版新课标B必修21.2.3空间中的垂直关系图文课件ppt，共12页。PPT课件主要包含了空间两条直线垂直，直线与平面垂直，求证lm等内容，欢迎下载使用。

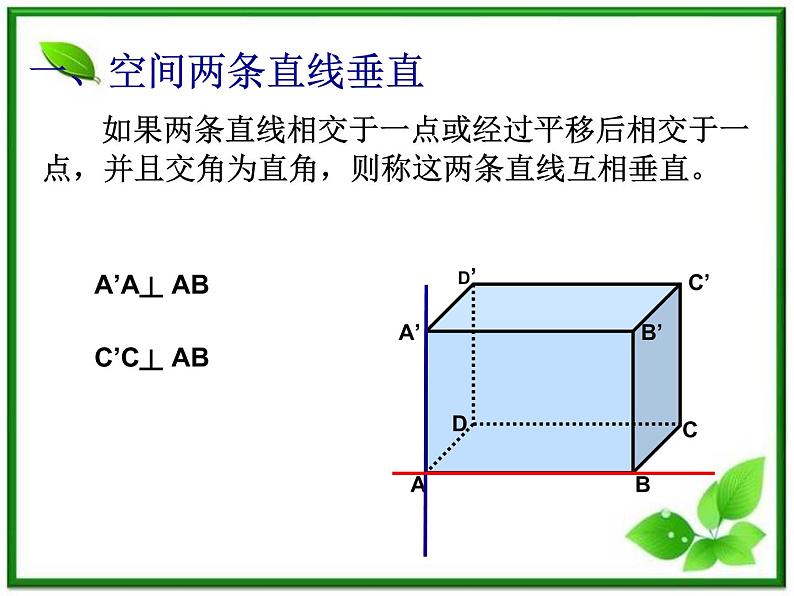
如果两条直线相交于一点或经过平移后相交于一点，并且交角为直角，则称这两条直线互相垂直。
如果一条直线AB和一个平面α相交于一点O，并且和这个平面内过交点O的任何直线都垂直，我们就说这条直线和这个平面垂直。
这条直线叫做平面的垂线，这个平面叫做直线的垂面。
交点叫做垂足,垂线上一点到垂足间的线段,叫做这个点到这个平面的垂线段,垂线段的长度叫做这个点到平面的距离。
如果一条直线垂直于一个平面，那么它就和平面内的任意一条直线垂直。
直线与平面垂直的判定定理
如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直。
如果在两条平行直线中,有一条垂直于平面,那么另一条直线和这个平面的位置关系如何？
问题：如果两条直线垂直于同一个平面，那么这两条直线是什么位置关系？
如果两条直线垂直于同一个平面,那么这两条直线平行。
直线与平面垂直的性质定理
已知：直线l⊥平面α，直线m⊥平面α,垂足分别为A、B。
证明：假设直线m不与直线l平行，
过直线m与平面α的交点B，作直线m’//l ,
由直线与平面垂直的判定定理的推论可知
设m和m’确定的平面为β，α与β的交线为a,
因为直线m和m’都垂直于平面α.
所以直线m和m’都垂直于交线a.
因为在同一平面内，通过直线上一点与已知直线垂直的直线不可能有两条。
所以直线m和m必重合，即l//m
定义 如果一条直线AB和一个平面α相交于一点O，并且和这个平面内过交点O的任何直线都垂直，我们就说这条直线和这个平面垂直。
判定定理 如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直。
推论 如果在两条平行直线中,有一条垂直于平面,那么另一条直线也和这个平面垂直。
性质定理 如果两条直线垂直于同一个平面,那么这两条直线平行.
例1过一点和已知平面垂直的直线只有一条。
已知：平面α和一点P。
求证：过点P与平面α垂直的直线只有一条。
例2 有一根旗杆AB高8m，它的顶端A挂着两条长10m的绳子，拉紧绳子，并把它的下端放在地面上的两点C,D（和旗杆脚不在同一条直线上），如果这两点都和旗杆脚B的距离是6m，那么旗杆就和地面垂直，为什么？