
数学必修21.2.3空间中的垂直关系当堂达标检测题
展开《空间中的垂直关系》
专题训练
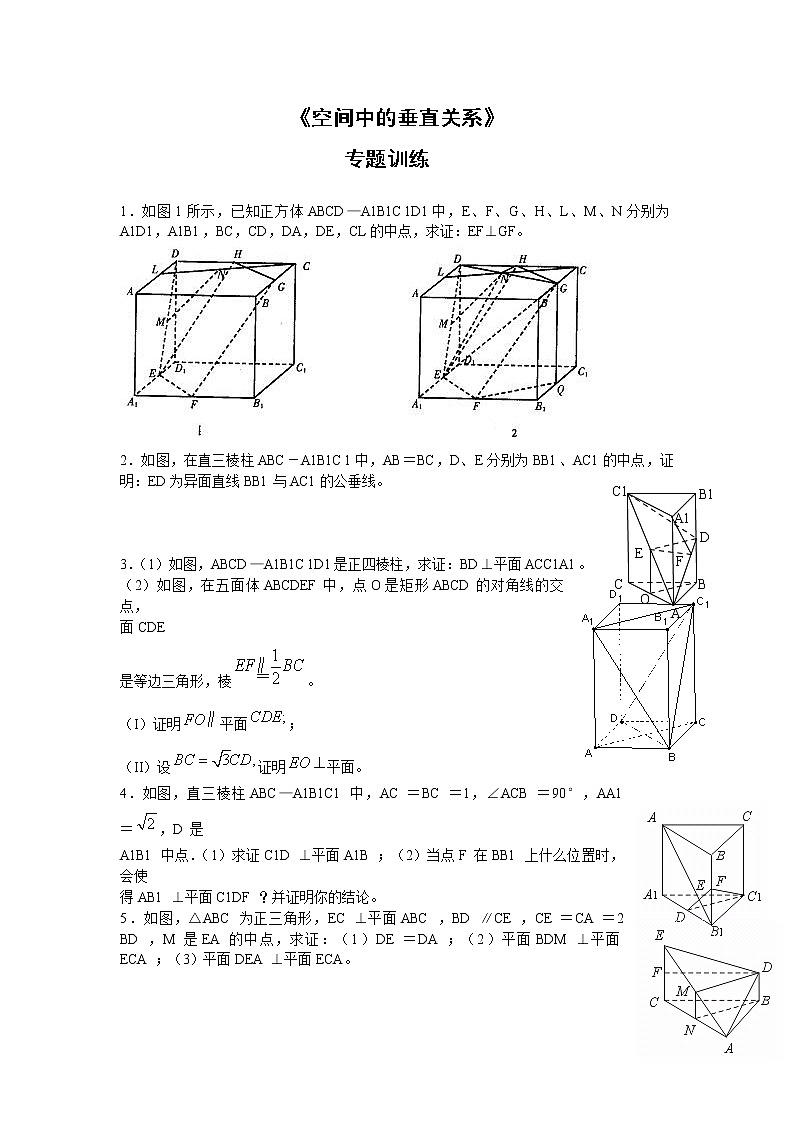
1.如图1所示,已知正方体ABCD—A1B1C1D1中,E、F、G、H、L、M、N分别为A1D1,A1B1,BC,CD,DA,DE,CL的中点,求证:EF⊥GF。
2.如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点,证明:ED为异面直线BB1与AC1的公垂线。
3.(1)如图,ABCD—A1B1C1D1是正四棱柱,求证:BD⊥平面ACC1A1。
(2)如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,
面CDE
是等边三角形,棱。
(I)证明平面;
(II)设证明平面。
4.如图,直三棱柱ABC—A1B1C1 中,AC =BC =1,∠ACB =90°,AA1 =,D 是
A1B1 中点.(1)求证C1D ⊥平面A1B ;(2)当点F 在BB1 上什么位置时,会使
得AB1 ⊥平面C1DF ?并证明你的结论。
5.如图,△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,CE =CA =2 BD ,M 是EA 的中点,求证:(1)DE =DA ;(2)平面BDM ⊥平面ECA ;(3)平面DEA ⊥平面ECA。
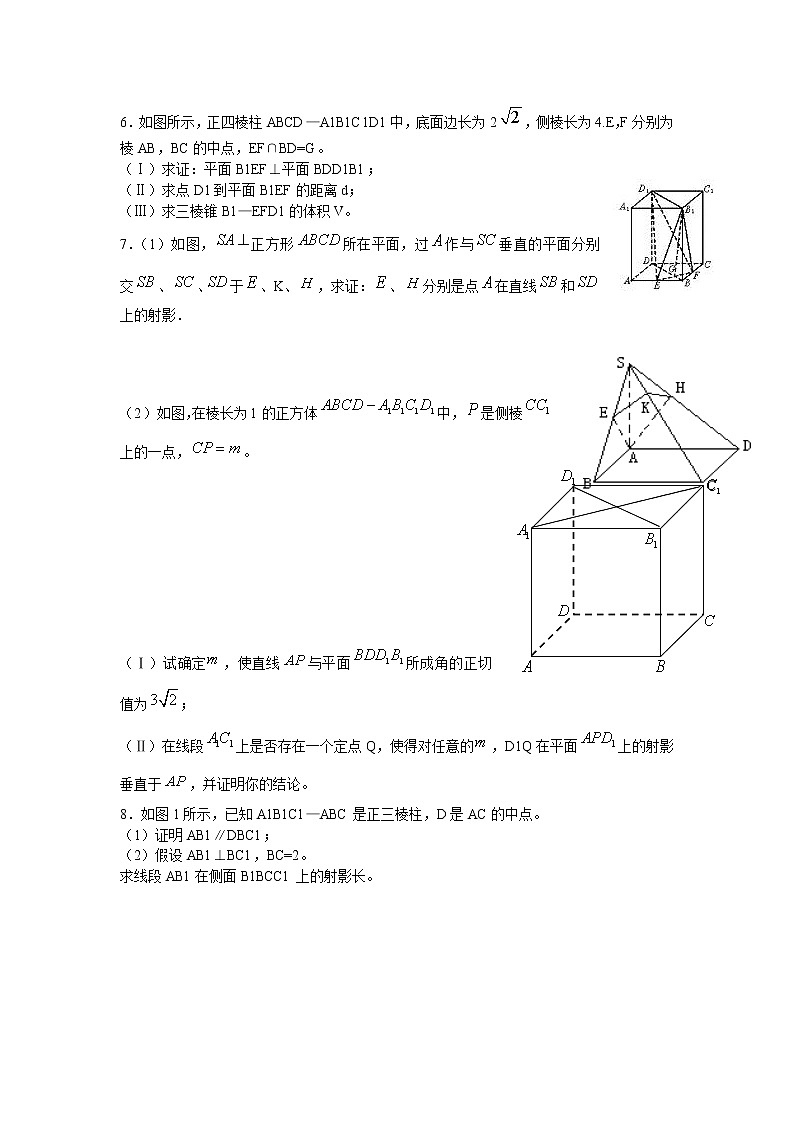
6.如图所示,正四棱柱ABCD—A1B1C1D1中,底面边长为2,侧棱长为4.E,F分别为棱AB,BC的中点,EF∩BD=G。
(Ⅰ)求证:平面B1EF⊥平面BDD1B1;
(Ⅱ)求点D1到平面B1EF的距离d;
(Ⅲ)求三棱锥B1—EFD1的体积V。
7.(1)如图,正方形所在平面,过作与垂直的平面分别交、、于、K、,求证:、分别是点在直线和上的射影.
(2)如图,在棱长为1的正方体中,是侧棱上的一点,。
(Ⅰ)试确定,使直线与平面所成角的正切值为;
(Ⅱ)在线段上是否存在一个定点Q,使得对任意的,D1Q在平面上的射影垂直于,并证明你的结论。
8.如图1所示,已知A1B1C1—ABC是正三棱柱,D是AC的中点。
(1)证明AB1∥DBC1;
(2)假设AB1⊥BC1,BC=2。
求线段AB1在侧面B1BCC1上的射影长。
9.已知是边长为的正三角形所在平面外一点,
,求异面直线与的距离。
10.如图,在空间四边形中,、、、分别是边、、
、的中点,对角线且它们所成的角为。
⑴求证:,⑵求四边形的面积。
11.如图(1)所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是图(2)的 (要求:把可能的图的序号都填上)
图(1)
图(2)
(2)命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥。
命题A的等价命题B可以是:底面为正三角形,且 的三棱锥是正三棱锥。
12.α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线.给出四个论断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: 。
答案:m⊥α,n⊥β,α⊥βm⊥n或m⊥n,m⊥α,n⊥βα⊥β
《空间中的垂直关系》答案
1.
证明:如图2,作GQ⊥B1C1于Q,连接FQ,则GQ⊥平面A1B1C1D1,且Q为B1C1的中点。
在正方形A1B1C1D1中,由E、F、Q分别为A1D1、A1B1、B1C1的中点可证明EF⊥FQ,
由三垂线定理得EF⊥GF。
2.证明:设O为AC中点,连接EO,BO,则EOC1C,又C1CB1B,所以EODB,
EOBD为平行四边形,ED∥OB。
∵AB=BC,∴BO⊥AC,
又平面ABC⊥平面ACC1A1,BO面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线。
点评:该题考点多,具有一定深度,但入手不难,逐渐加深,逻辑推理增强。
3.
证明:(1)∵ABCD—A1B1C1D1是正四棱柱,
∴CC1⊥平面ADCD,
∴BD⊥CC1
∵ABCD是正方形
∴BD⊥AC
又∵AC,CC1平面ACC1A1,
且AC∩CC1=C,
∴BD⊥平面ACC1A1。
(2)证明:
(I)取CD中点M,连结OM。
在矩形ABCD中, 又
则连结EM,于是四边形EFOM为平行四边形。
又平面CDE,且平面CDE,
平面CDE。
(II)连结FM。
由(I)和已知条件,在等边中,
且
因此平行四边形EFOM为菱形,从而。
平面EOM,从而
而所以平面
4.
分析:(1)由于C1D 所在平面A1B1C1 垂直平面A1B ,只要证明C1D 垂直交线A1B1 ,由直线与平面垂直判定定理可得C1D ⊥平面A1B。
(2)由(1)得C1D ⊥AB1 ,只要过D 作AB1 的垂线,它与BB1 的交点即为所求的F 点位置。
(1)证明:如图,∵ ABC—A1B1C1 是直三棱柱,
∴ A1C1 =B1C1 =1,且∠A1C1B1 =90°。
又 D 是A1B1 的中点,∴ C1D ⊥A1B1 。
∵ AA1 ⊥平面A1B1C1 ,C1D 平面A1B1C1 ,
∴ AA1 ⊥C1D ,∴ C1D ⊥平面AA1B1B。
(2)解:作DE ⊥AB1 交AB1 于E ,延长DE 交BB1 于F ,连结C1F ,则AB1 ⊥平面C1DF ,点F 即为所求。
事实上,∵ C1D ⊥平面AA1BB ,AB1 平面AA1B1B ,
∴ C1D ⊥AB1 .又AB1 ⊥DF ,DF C1D =D ,
∴ AB1 ⊥平面C1DF 。
5.
证明:(1)如图,取EC 中点F ,连结DF。
∵ EC ⊥平面ABC ,BD ∥CE ,得DB ⊥平面ABC 。
∴ DB ⊥AB ,EC ⊥BC。
∵ BD ∥CE ,BD =CE =FC ,则四边形FCBD 是矩形,DF ⊥EC。
又BA =BC =DF ,
∴ Rt△DEF ≌Rt△ABD ,所以DE =DA。
(2)取AC 中点N ,连结MN 、NB ,
∵ M 是EA 的中点,
∴ MN EC。
由BD EC ,且BD ⊥平面ABC ,可得四边形MNBD 是矩形,于是DM ⊥MN。
∵ DE =DA ,M 是EA 的中点,
∴ DM ⊥EA .又EA MN =M ,
∴ DM ⊥平面ECA ,而DM 平面BDM ,则平面ECA ⊥平面BDM。
(3)∵ DM ⊥平面ECA ,DM 平面DEA ,
∴ 平面DEA ⊥平面ECA。
6.
(Ⅰ)证法一:连接AC。
∵正四棱柱ABCD—A1B1C1D1的底面是正方形。
∴AC⊥BD,又AC⊥D1D,故AC⊥平面BDD1B1
∵E,F分别为AB,BC的中点,故EF∥AC,∴EF⊥平面BDD1B1
∴平面B1EF⊥平面BDD1B1。
证法二:∵BE=BF,∠EBD=∠FBD=45°,∴EF⊥BD.
∴平面B1EF⊥平面BDD1B1。
(Ⅱ)解:在对角面BDD1B1中,作D1H⊥B1G,垂足为H
∵平面B1EF⊥平面BDD1B1,且平面B1EF∩平面BDD1B1=B1G,
∴D1H⊥平面B1EF,且垂足为H,∴点D1到平面B1EF的距离d=D1H。
解法一:在Rt△D1HB1中,D1H=D1B1·sinD1B1H,
∵D1B1=A1B1=4,
sinD1B1H=sinB1GB=,
∴d=D1H=4·
解法二:∵△D1HB∽△B1BG,∴
∴d=D1H=。
解法三:如图所示,连接D1G,则三角形D1GB1的面积等于正方形DBB1D1面积的一半.即B1G·D1H=BB12。
∴d=。
(Ⅲ)·d·.
7.
证明:∵ 面,∴ ,
∵ 为正方形,∴ ,
∵ 与相交,∴ 面,面,
∴ .
由已知面,且面,
∴ ,
∵ ,∴ 面,面,∴ ,
即 为点在直线上的射影,
同理可证得为点在直线上的射影。
(2)
解法1:(Ⅰ)连AC,设AC与BD相交于点O,AP与平面相交于点,连结OG,
因为PC∥平面,平面∩平面APC=OG,
故OG∥PC,所以OG=PC=。
又AO⊥BD,AO⊥BB1,所以AO⊥平面,
故∠AGO是AP与平面所成的角。
在Rt△AOG中,tanAGO=,即m=。
所以,当m=时,直线AP与平面所成的角的正切值为。
(Ⅱ)可以推测,点Q应当是AICI的中点O1,
因为D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP平面ACC1A1,故 D1O1⊥AP。
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。
8.
证明:(1)如图2所示,∵A1B1C1—ABC是正三棱柱,
∴四边形B1BCC1是矩形。
连结B1C,交BC1于E,则BE=EC。
连结DE,在△AB1C中,∵AD=DC,
∴DE∥AB1,又因为AB1平面DBC1,DE平面DBC1,∴AB1∥平面DBC1。
(2)作AF⊥BC,垂足为F。因为面ABC⊥面B1BCC1,
∴AF⊥平面B1BCC1。连结B1F,则B1F是AB1在平面B1BCC1内的射影。
∵BC1⊥AB1,∴BC1⊥B1F。
∵四边形B1BCC1是矩形,∴∠B1BF=∠BCC1=90°,又∠FB1B=∠C1BC,∴△B1BF∽△BCC1,则==。
又F为正三角形ABC的BC边中点,因而B1B2=BF·BC=1×2=2。
于是B1F2=B1B2+BF2=3,∴B1F=,即线段AB1在平面B1BCC1内的射影长为。
9.
解析:分别取、
中点、,连
结(图⑴)。
连结、(图
⑵)
∵,
为公共边,,
∴≌ ∴
∵点为中点 ∴ 同理:(图⑶)
又,,
∴即为异面直线与的公垂线段
如图⑵,在中,,,,
∴ ∴异面直线与的距离。
点评:求异面直线的距离,必须先找到两条异面直线的公垂线段。
10.
解析:⑴在中,、分别是边、的中点,∴∥,
在中,、分别是边、的中点,∴∥,
∴∥且,
同理:∥且,
∵,∴,
∴四边形为菱形,∴。
⑵∵∥,∥,
∴(或的补角)即为异面直线与所成的角,
由已知得:(或),
∴四边形的面积为:。
11.
图(1)
图(2)
答案:②③
解析:∵面BFD1E⊥面ADD1A1,所以四边形BFD1E在面ADD1A1上的射影是③,同理,在面BCC1B1上的射影也是③。
过E、F分别作DD1和CC1的垂线,可得四边形BFD1E在面DCC1D1上的射影是②,同理在面ABB1A1,面ABCD和面A1B1C1D1上的射影也是②。
(2)
解析:要使命题B与命题A等价,则只需保证顶点在底面上的射影S是底面正三角形的外心即可,因此,据射影定理,得侧棱长相等。
12.
答案:m⊥α,n⊥β,α⊥βm⊥n或m⊥n,m⊥α,n⊥βα⊥β
2020-2021学年第十一章 立体几何初步11.4 空间中的垂直关系11.4.1 直线与平面垂直达标测试: 这是一份2020-2021学年第十一章 立体几何初步11.4 空间中的垂直关系11.4.1 直线与平面垂直达标测试,共23页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
高中数学人教版新课标B必修21.2.3空间中的垂直关系达标测试: 这是一份高中数学人教版新课标B必修21.2.3空间中的垂直关系达标测试,共3页。
高中数学1.2.3空间中的垂直关系随堂练习题: 这是一份高中数学1.2.3空间中的垂直关系随堂练习题,共4页。













