高中数学人教版新课标B必修21.2.3空间中的垂直关系达标测试

空间中的垂直关系

【目标要求】

1.了解直线和平面垂直的概念，掌握直线和平面垂直的判定定理.

2.使学生掌握两个平面垂直的性质定理及其证明．并能应用判定定理和性质定理解决简单问题；

3.了解射影等有关的概念，了解三垂线定理及其逆定理.

【巩固教材——稳扎马步】

1.直线l与平面内的两条直线都垂直，则直线l与平面的位置关系是 （   ）

A.平行     B.垂直      C.在平面内     D.无法确定

2.菱形ABCD在平面α内，PC⊥α，则PA与对角线BD的位置关系是　　　　　（    ）

A.平行   B.斜交    C.垂直相交    D.垂直但不相交

3.平面α上有不共线三点到平面β的距离相等，则α与β的位置关系为　　　　　（    ）

A.平行   B.相交    C.平行或相交    D.垂直

4.下列说法正确的是     （   ）

A.平面内的一条直线和平面内的无数条直线垂直，则平面⊥平面

B.过平面外一点P有且只有一个平面和平面垂直

C.直线l∥平面，l⊥平面，则⊥

D.垂直于同一平面的两个平面平行

【重难突破——重拳出击】

5.已知l⊥，m，则下面说法中正确的是                        （　　）

  ①∥则l⊥m      ②⊥则l∥m    ③l∥m则⊥   ④l⊥m则∥

A.①②           B.③④         C.②④         D.①③

6.设P、Q、R分别是长方体的棱AA1、AB、AD上异于点A的任意一点，则△PQR的形状

为　　　　　　　　　　　　　　　　　　　　　（    ）

A.直角三角形   B.锐角三角形    C.钝角三角形    D.以上都有可能

7.下列说法中正确的个数是                                           （     ）

①若直线a//平面，平面⊥平面，则a⊥;

②平面⊥平面，平面⊥平面γ，则⊥γ；

③直线a⊥平面，平面⊥平面，则a//；

④ 平面//平面，直线a平面，则a//．                    

A.1        B.2        C.3               D.4

8.若有平面与，且，则下列说法不正确的是      （     ）

A.过点且垂直于的直线平行于         B.过点且垂直于的平面垂直于

C.过点且垂直于的直线在内           D.过点且垂直于的直线在内

9.下面各选项中，不正确是                                          （    ）

1. 平行于同一直线的两个平面平行  

B.平行于同一平面的两个平面平行

   C.一条直线与两个平行平面中的一个相交，那么这条直线必和另一个平面相交

   D.垂直于同一直线的两个平面平行

10.过空间一点的三条直线两两垂直则由它们确定的平面中互相垂直的有（   ）

A.0对    B.1对   C.2对       D.3对

11.两个平面互相垂直，一条直线和其中一个平面平行，则这条直线和另一个平面的位置关

系是（   ）

A.垂直      B.相交或平行     C.平行或垂直         D.不能确定

12.经过平面外的两点作与该平面垂直的平面，那么         （    ）

A.有且只有1个      B.无数个    C. 1个或无数个        D. 最多有2个

【巩固提高——登峰揽月】

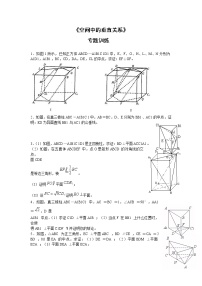
13.在正方体ABCD—A1B1C1D1，G为CC1的中点，O为底面ABCD的中心.

 求证：A1O⊥平面GBD.

14. 已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点.

（1）求证：MN⊥CD.

（2）若∠PDA=45°，求证MN⊥面PCD.

【课外拓展——超越自我】

15. 如图，在正方体ABCD—A1B1C1D1中，已知P，Q，R，S分别为棱A1D1，A1B1，AB，BB1的中点，求证：平面PQS⊥平面B1RC.

空间中的垂直关系答案：

【巩固教材——稳扎马步】

1.D  2.D  3.C  4.C 

【重难突破——重拳出击】

5.D 6.B  7.A  8.D  9.A 10.D  11.D 12.C

【巩固提高——登峰揽月】

13. 证明：

14. 证明：

【课外拓展——超越自我】

15. 证明：连结BC1交B1C于O，则O为BC1的中点

连结RO，AC1，∵R是AB的中点  ∴RO∥AC1

∵P,Q分别为A1D1，A1B1的中点，易知A1C1⊥PQ

∴AC1⊥PQ