高端精品高中数学一轮专题-等比数列（精讲）（带答案）教案

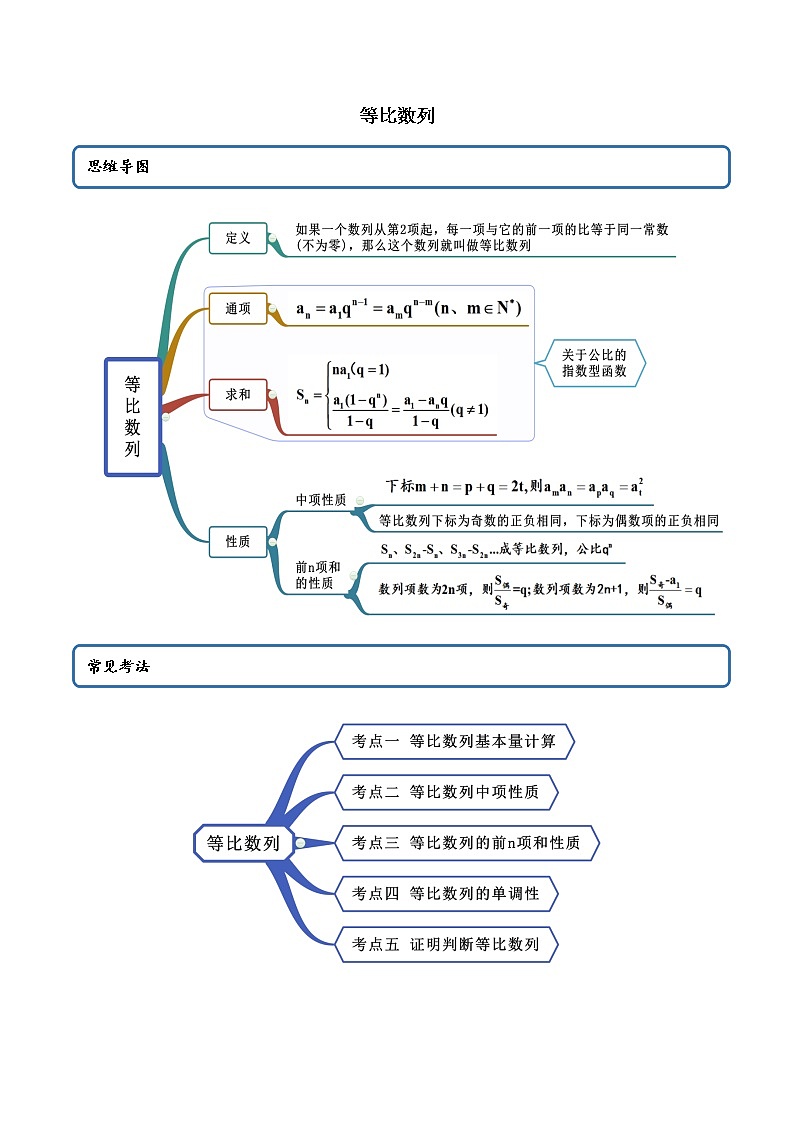
等比数列

考点一 等比数列基本量计算

【例1】（1）在等比数列中，，，则公比的值为（    ）

A． B．或1 C．－1 D．或－1

（2）已知各项均为正数的等比数列的前4项和为15，且，则（  ）

A．16 B．8 C．4 D．2

（3）等比数列的前项和，则=（   ）

A．-1 B．3 C．-3 D．1

【答案】（1）B（2）C（3）C

【解析】（1）由题意，解得或．故选：B．

【答案】C

（2）设正数的等比数列{an}的公比为，则，

解得，，故选C．

（3）因为数列是等比数列故满足 ， ，

代入得到 故答案选C．

【一隅三反】

1．已知是等比数列，a1=2,a4=,则公比q=（    ）

A． B．-2 C．2 D．

【答案】D

【解析】∵是等比数列，∴，∴．故选：D．

2．已知数列满足，若，则等于（    ）

A．1 B．2 C．64 D．128

【答案】C

【解析】因为数列满足，所以该数列是以为公比的等比数列，又，所以，即；故选C.

3．各项都是正数的等比数列中，成等差数列，则公比的值为（    ）

A． B．

C． D．或

【答案】B

【解析】由题得，所以，

因为是各项都是正数的等比数列，所以，所以.故选：B

4．已知各项均为正数的等比数列，且成等差数列，则的值是（    ）

A． B． C． D．

【答案】D

【解析】各项均为正数的等比数列的公比设为q，则q>0，

由成等差数列，可得，即，

所以，解得或（舍），

所以.故选：D.

5．设正项等比数列的前项和为，，则公比等于（    ）

A． B． C． D．

【答案】A

【解析】因为，所以

所以，即

因为，所以故选：A

考点二 等比数列中项性质

【例2】（1）等比数列的各项均为正数，且，则（    ）

A． B． C． D．

（2）在等比数列中，若，则（    ）

A． B． C． D．

【答案】（1）B（2）B

【解析】（1）由等比数列的性质可得：，所以.

则故选B.

（2）由等比中项的性质可得，解得，因此，.故选：B.

【一隅三反】

1．在等比数列中，是方程的根，则（    ）

A． B．

C． D．

【答案】A

【解析】由题得所以，因为，

所以所以.故答案为A

2．若三个数1，2，m成等比数列，则实数（    ）

A．8 B．4 C．3 D．2

【答案】B

【解析】因为为等比数列，故即，故选：B.

3．已知实数成等比数列，则椭圆的离心率为（    ）

A． B．2 C．或2 D．或

【答案】A

【解析】∵1，m，9构成一个等比数列，∴m2=1×9，则m=±3．

当m=3时，圆锥曲线+y2=1是椭圆，它的离心率是=；

当m=﹣3时，圆锥曲线+y2=1是双曲线，故舍去，则离心率为．故选A．

考点三 等比数列的前n项和性质

【例3】已知数列{an}是等比数列，Sn为其前n项和，若a1＋a2＋a3=4，a4＋a5＋a6=8，则S12=（    ）

A．40 B．60

C．32 D．50

【答案】B

【解析】由等比数列的性质可知，数列S3，S6−S3，S9−S6，S12−S9是等比数列，即数列4,8，S9−S6，S12−S9是等比数列，因此S12=4＋8＋16＋32=60，选B．

【一隅三反】

1．已知是各项都为正数的等比数列，是它的前项和，若，，则（    ）

A． B．90 C．105 D．106

【答案】C

【解析】由等比数列的性质得成等比数列，

所以成等比数列，所以.故选：C

2．等比数列的前n项和为，若，则（    ）

A． B． C． D．

【答案】C

【解析】因为数列为等比数列，则，，成等比数列，

设，则，则，

故，所以，得到，所以.故选：C.

3．若等比数列{an}的前n项和为Sn，且S5＝10，S10＝30，则S20＝（    ）

A．80 B．120 C．150 D．180

【答案】C

【解析】因为数列是等比数列，故可得依然成等比数列，

因为，故可得，故该数列的首项为，公比为2，

故可得.故选：.

4．设是等比数列，且，，则（    ）

A．12 B．24 C．30 D．32

【答案】D

【解析】设等比数列的公比为，则，

，

因此，.故选：D.

考点四 等比数列的单调性

【例4】已知数列满足，.

（1）求证：数列是等比数列；

（2）求数列的通项公式.

【答案】（1）证明见解析；（2）.

【解析】（1），，

因此，数列是等比数列；

（2）由于，所以，数列是以为首项，以为公比的等比数列，，因此，.

【一隅三反】

1．已知为等比数列，，，以表示的前项积，则使得达到最大值的是（    ）

A．4 B．5 C．6 D．7

【答案】A

【解析】为等比数列，，，

，，，，．

故是一个减数列，前4项都大于1，从第五项开始小于1，

以表示的前项积，则使得达到最大值的是4，

故选：．

2．已知单调递减的等比数列中，，则该数列的公比的取值范围是（    ）

A． B． C． D．

【答案】D

【解析】因为等比数列单调递减，所以，，

因为，所以，

又因为，所以，所以，故选：D

3．若是公比为的等比数列，记为的前项和，则下列说法正确的是（    ）

A．若是递增数列，则

B．若是递减数列，则

C．若，则

D．若，则是等比数列

【答案】D

【解析】A选项中，，满足单调递增，故A错误；

B选项中，，满足单调递减，故B错误；

C选项中，若，则，故C错误；

D选项中，，所以是等比数列.故D正确.

故选：D.

4．设等比数列的公比为，其前项的积为，并且满足条件，，．给出下列结论：

①；②；③的值是中最大的；④使成立的最大自然数等于198

其中正确的结论是（    ）

A．①③ B．①④ C．②③ D．②④

【答案】B

【解析】①，，．

，．

又，，且．，即①正确；

②，，即，故②错误；

③由于，而，故有，故③错误；

④中，

，故④正确．

正确的为①④，

故选：．

考点五 证明判断等比数列

【例5】已知正项数列的前项和为，若数列是公差为的等差数列，且是等差中项.

（1）证明数列等比数列；

（2）求数列的通项公式.

【答案】（1）证明见解析（2）

【解析】（1）因为数列是公差为的等差数列，所以，

故，所以，所以数列是公比为3的等比数列.

（2）因为是的等差中项，所以，所以，

解得，数列的通项公式为.

【一隅三反】

1．数列（   ）

A．既不是等差数列又不是等比数列 B．是等比数列但不是等差数列

C．既是等差数列又是等比数列 D．是等差数列但不是等比数列

【答案】D

【解析】数列是无穷数列，从第二项开始起，每一项与它前一项的差都等于常数，符合等差数列的定义，所以数列是等差数列，根据等比数列的定义可知，等比数列中不含有为的项，所以数列不是等比数列，故选D.

2．已知数列是等比数列，那么下列数列一定是等比数列的是（   ）

A． B． C． D．

【答案】AD

【解析】时，，数列不一定是等比数列，

时，，数列不一定是等比数列，

由等比数列的定义知和都是等比数列．

故选AD．

3．已知数列满足，．设．

（1）证明：数列为等比数列；

（2）求的通项公式．

【答案】（1）详见解析；（2）．

【解析】（1），，由条件可得，即，又，

所以是首项为1，公比为2的等比数列．

（2）由（1）可得，，所以．