高端精品高中数学一轮专题-数学归纳法（精讲）教案

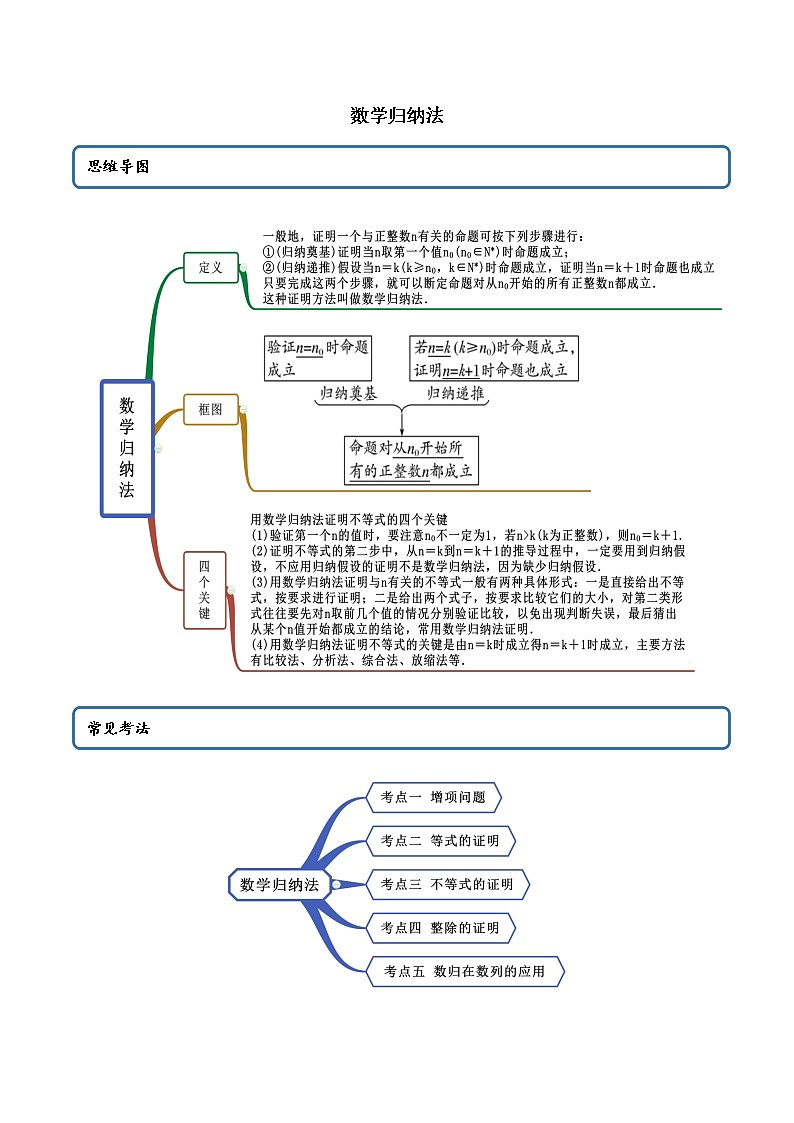
这是一份高端精品高中数学一轮专题-数学归纳法（精讲）教案，共5页。教案主要包含了增项问题，等式的证明，不等式的证明，整除问题，数归在数列的应用等内容，欢迎下载使用。
数学归纳法考点一 增项问题【例1】用数学归纳法证明的过程中，当从到时，等式左边应增乘的式子是（    ）A． B．C． D． 【一隅三反】1．()，那么共有（    ）项.A． B． C． D．以上都不对 2．用数学归纳法证明不等式的过程中，由递推到时，不等式左边（    ）A．增加了     B．增加了C．增加了  D．增加了 3．用数学归纳法证明等式（n∈N*）的过程中，第二步假设n=k时等式成立，则当n=k+1时应得到（ ）A．B．C．D．4．用数学归纳法证明“”，由到时，不等式左边应添加的项是（    ）A． B．C． D． 考点二 等式的证明【例2】．用数学归纳法证明.   【一隅三反】1．用数学归纳法证明等式.  2．用数学归纳法证明：.  考点三 不等式的证明【例3】用数学归纳法证明：.   【一隅三反】1．证明：不等式，恒成立.  2．试用数学归纳法证明.    考点四 整除问题【例4】用数学归纳法证明：能被133整除．   【一隅三反】1．求证：能被整除．   2．用数学归纳法证明：对任意正整数能被9整除．    考点五 数归在数列的应用【例5】设数列的前项和为，且对任意的正整数都满足．（1）求，，的值，猜想的表达式；（2）用数学归纳法证明（1）中猜想的的表达式的正确性．   【一隅三反】1．已知数列的前项和为，，且.（1）求、、；（2）由（1）猜想数列的通项公式，并用数学归纳法证明．    2．已知等比数列的公比，且，是，的等差中项，数列满足：数列的前项和为．（1）求数列、的通项公式；（2）数列满足：，，证明    3．若，且.（1）求，， ，，（2）归纳猜想通项公式，用数学归纳法证明.