





高中数学一轮总复习课件2.6 对数与对数函数
展开1.理解对数的概念和运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数.2.通过具体实例,了解对数函数的概念.3.能用描点法或借助计算工具画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点.4.知道对数函数y=lgax与指数函数y=ax互为反函数(a>0,且a≠1).
作为另一种重要的基本初等函数,对数函数比指数函数在高考中更加常见,除了基本的对数运算、图象与性质外,对数运算还经常与其他知识综合考查.解题时要重视对数的真数大于0这一条件,重视其图象以及单调性等性质的应用,提升数学抽象素养与应用数形结合思想解题的能力.
第一环节 必备知识落实
第二环节 关键能力形成
第三环节 学科素养提升
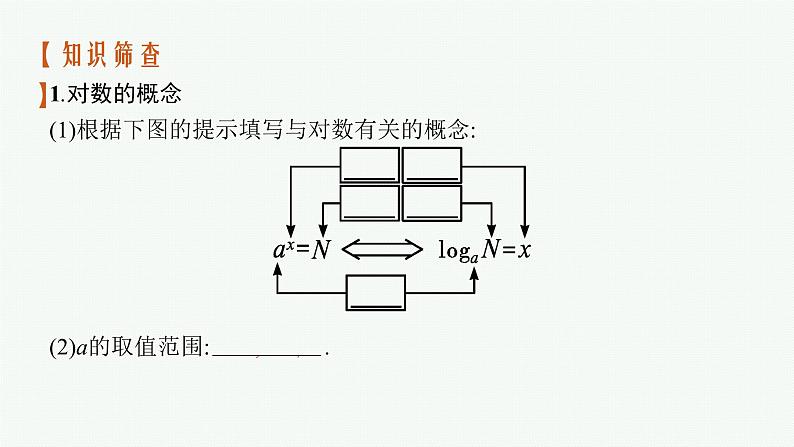
1.对数的概念(1)根据下图的提示填写与对数有关的概念: (2)a的取值范围: a>0,且a≠1 .
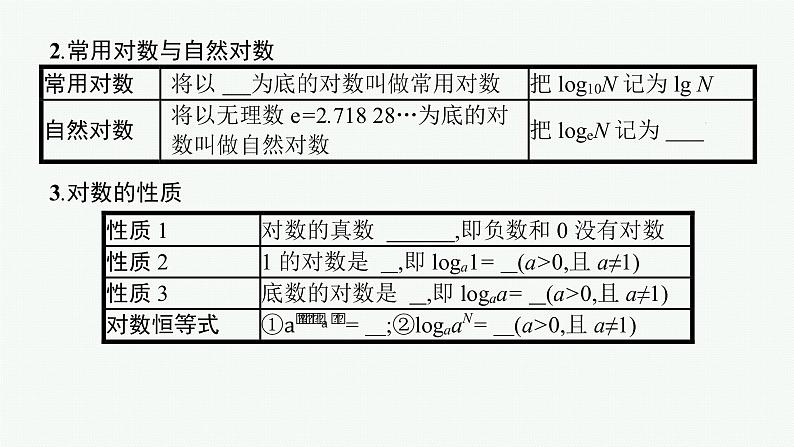
2.常用对数与自然对数
6.对数函数的图象与性质
7.反函数对数函数y=lgax(a>0,且a≠1)与指数函数y=ax(a>0,且a≠1)互为反函数.互为反函数的两个函数的图象关于直线 y=x 对称.它们的定义域与值域正好互换.
1.换底公式的两个重要结论
其中a>0,且a≠1,b>0,且b≠1,m≠0,n∈R.
2.对数函数的图象与底数大小的比较如图,作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数,故0
当a>1时,函数y=lgax的图象为选项B,D中过点(1,0)的曲线,此时函数y=-x+a的图象与y轴的交点的纵坐标a应满足a>1,选项B,D中的图象都不符合要求;当0
当x=2时,函数y=lga(x-1)+2(a>0,且a≠1)的值为2,所以图象恒过定点(2,2).
解题心得对数运算的一般思路:(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后用对数的运算性质化简合并.(2)将对数式化为同底数对数的和、差、倍数运算,逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
(2)原式=(lg 2)2+(1+lg 5)lg 2+lg 52=(lg 2+lg 5+1)lg 2+2lg 5=(1+1)lg 2+2lg 5=2(lg 2+lg 5)=2.
例2 (1)已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=ln(x+1),则函数f(x)的大致图象为( )
先作出当x≥0时,f(x)=ln(x+1)的图象,显然图象经过点(0,0),再作此图象关于y轴对称的图象,可得函数f(x)在R上的大致图象,如选项C中图象所示.
解题心得应用对数型函数的图象可求解的问题:(1)对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想.(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.
对点训练2(1)已知函数y=lga(x+c)(a,c为常数,其中a>0,a≠1)的图象如图,则下列结论成立的是( ) A.a>1,c>1B.a>1,0
A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)
命题角度3 对数型函数的综合问题例5 已知函数f(x)=lga(ax-1)(a>0,且a≠1).(1)求f(x)的定义域;(2)讨论函数f(x)的单调性.
解 (1)由ax-1>0,得ax>1.当a>1时,x>0;当0
且y=lg2x在区间(0,+∞)内单调递增,所以lg23>lg2e>lg22=1,即c>a>1.因为y=ln x在区间(0,+∞)内单调递增,且b=ln 2,所以ln 2
(2)若不等式lgx(2x2+1)
对数型复合函数的单调性与奇偶性问题
命题角度1 对数型复合函数的单调性问题典例1 求下列函数的单调区间;
解题提示本题主要考查复合函数单调区间的求法,求解时要先求函数的定义域.
解题心得对数型复合函数单调性的求解策略(1)对数型复合函数一般可分两类:一类是对数函数为外函数,即y=lgaf(x) (a>0,且a≠1)型;另一类是对数函数为内函数,即y=f(lgax)(a>0,且a≠1)型.(2)对于y=lgaf(x)(a>0,且a≠1)型函数的单调性,有以下结论:y=lgaf(x)(a>0,且a≠1)的单调性与u=f(x)(f(x)>0)的单调性在a>1时相同,在0
高考复习 2.6 对数与对数函数课件PPT: 这是一份高考复习 2.6 对数与对数函数课件PPT,共47页。PPT课件主要包含了x=logaN,nlogaM,0+∞,减函数,增函数,y=x,答案D,答案B,答案A,3+∞等内容,欢迎下载使用。
高考数学一轮复习第2章2.6对数与对数函数课件: 这是一份高考数学一轮复习第2章2.6对数与对数函数课件,共46页。PPT课件主要包含了内容索引,必备知识预案自诊,知识梳理,nlogaM,0+∞,增函数,减函数,ylogax,常用结论,考点自诊等内容,欢迎下载使用。
新教材高考数学一轮复习第2章2.6对数与对数函数课件: 这是一份新教材高考数学一轮复习第2章2.6对数与对数函数课件,共46页。PPT课件主要包含了内容索引,必备知识预案自诊,知识梳理,nlogaM,0+∞,增函数,减函数,ylogax,常用结论,考点自诊等内容,欢迎下载使用。












