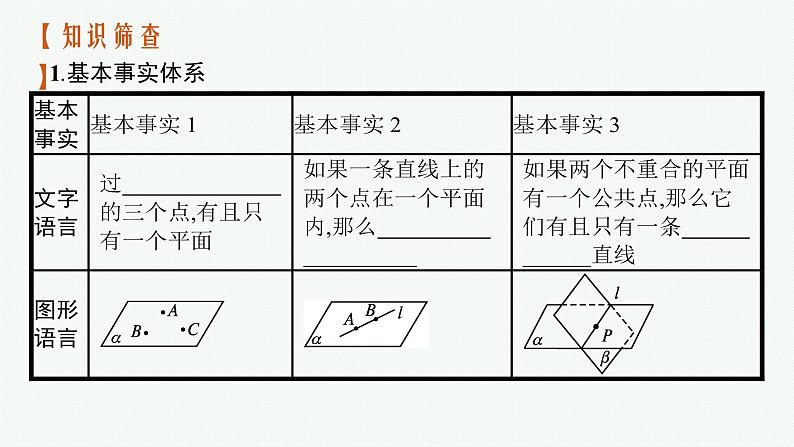
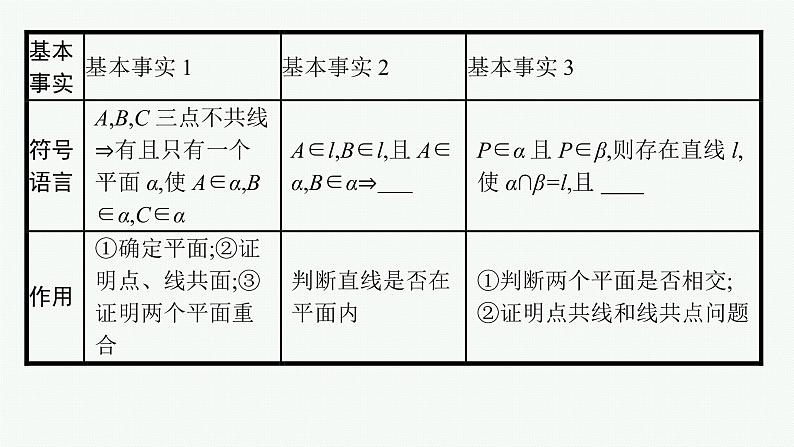
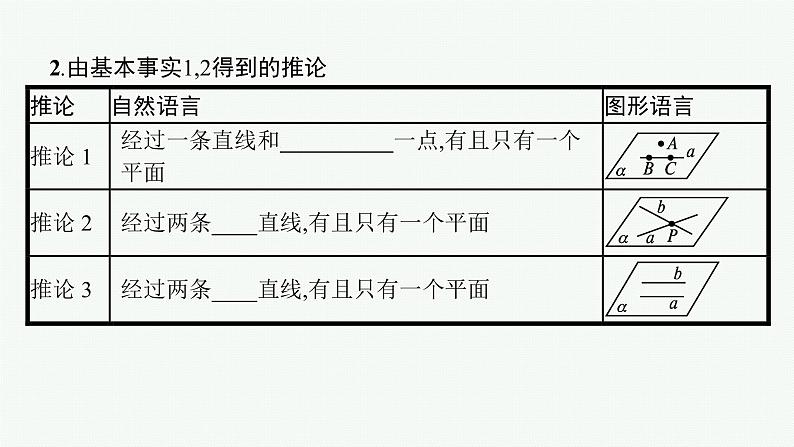
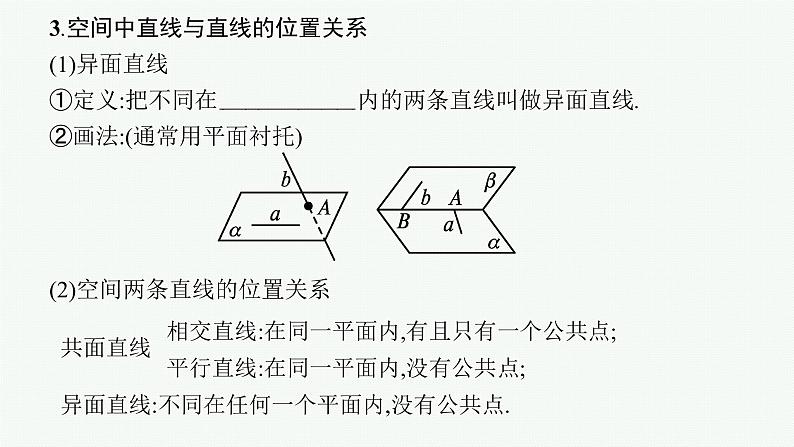
高中数学一轮总复习课件7.2　空间点、直线、平面之间的位置关系

这是一份高中数学一轮总复习课件7.2　空间点、直线、平面之间的位置关系，共47页。PPT课件主要包含了课标要求，备考指导，内容索引，知识筛查，基本事实体系，知识巩固，ACBD等内容，欢迎下载使用。
1.借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义.2.了解基本事实1—4和等角定理.
本节的基本事实是立体几何位置关系的基础,复习时应结合图形和符号语言理解记忆.能准确把握对点、线、面及关系的逻辑表达,为后面空间位置关系的证明打好基础,培养空间想象的数学素养.
第一环节　必备知识落实
第二环节　关键能力形成
第三环节　学科素养提升
2.由基本事实1,2得到的推论
3.空间中直线与直线的位置关系(1)异面直线①定义:把不同在任何一个平面内的两条直线叫做异面直线.②画法:(通常用平面衬托)
(2)空间两条直线的位置关系
(3)重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A∉α,B∈α,l⊂α,B∉l⇒AB与l是异面直线(如图).
问题思考分别在不同平面内的两条直线一定是异面直线吗?
不一定,如图,虽然有a⊂α,b⊂β,即a,b分别在两个不同的平面内,但是因为a∩b=O,所以a与b不是异面直线.
4.空间中直线与平面的位置关系
5.空间中平面与平面的位置关系
温馨提示平面与平面之间无特别说明,一般不讲“重合”.
6.基本事实4与等角定理(1)基本事实4
(2)等角定理如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
温馨提示定理中的两个角的三种位置情况:(1)两个角的两条边分别对应平行且方向相同,此时两个角相等;(2)两个角的两条边分别对应平行且方向相反,此时两个角相等;(3)两个角的两条边分别对应平行,且其中一条边方向相同,另一条边方向相反,此时两个角互补.
1.下列说法正确的画“√”,错误的画“×”.(1)两个不重合的平面只能把空间分成四个部分.(　　)(2)两个平面α,β有一个公共点A,就说α,β相交于A点,记作α∩β=A.(　　)(3)已知a,b是异面直线,直线c平行于直线a,则c与b不可能平行.(　　)(4)如果两个不重合的平面α,β有一条公共直线a,那么平面α,β相交,并记作α∩β=a.(　　)(5)若a,b是两条直线,α,β是两个平面,且a⊂α,b⊂β,则a,b是异面直线.(　　)
2.在空间中可以确定一个平面的条件是(　　)A.两条直线B.一点和一条直线C.三个点D.一个梯形
A中,若两条直线是异面直线,则不能确定一个平面;B中,若点在直线上,则不能确定一个平面;C中,若三个点在同一条直线上,则不能确定一个平面;D中,梯形有两条边平行,而两条平行直线能确定一个平面.
3.如图,在正方体ABCD-A1B1C1D1中,E,F分别为BC,BB1的中点,则下列直线中与直线EF相交的是(　　)A.直线AA1B.直线A1B1C.直线A1D1D.直线B1C1
只有B1C1与EF在同一平面内,且相交,选项A,B,C中直线与EF都是异面直线,故选D.
4.设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个结论:①P∈a,P∈α⇒a⊂α;②a∩b=P,b⊂β⇒a⊂β;③a∥b,a⊂α,P∈b,P∈α⇒b⊂α;④α∩β=b,P∈α,P∈β⇒P∈b.其中正确的结论是　　　　　.(填序号) 
①直线a与平面α可能相交于点P,故①不正确;②直线a与平面β可能相交,故②不正确;③④正确.
5.如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则 (1)当AC,BD满足条件　　　　　　　时,四边形EFGH为菱形; (2)当AC,BD满足条件　　　　　　　　　　时,四边形EFGH为正方形.
AC=BD,且AC⊥BD
命题角度1 证明点、线共面问题例1　已知一条直线与另外三条互相平行的直线都相交,证明:这四条直线共面.
证明 如图所示.(方法一)∵a∥b,∴a,b确定平面α.又l∩a=A,l∩b=B,∴l上有两点A,B在α内,即直线l⊂α.∴a,b,l共面.同理,a,c,l共面,即c也在a,l确定的平面内.故a,b,c,l共面.
(方法二)∵a∥b,∴a,b确定平面α.又A∈a,B∈b,∴AB⊂α,即l⊂α.又b∥c,∴b,c确定平面β.而B∈b,C∈c,∴BC⊂β,即l⊂β.∴b,l⊂α,b,l⊂β,而b∩l=B,∴α与β重合,故a,b,c,l共面.
命题角度2 证明点共线例2　如图,△ABC在平面α外,AB∩α=P,AC∩α=Q,BC∩α=R.求证:P,Q,R三点共线.
证明 (方法一)∵AB∩α=P,∴P∈AB,P∈α.又AB⊂平面ABC,∴P∈平面ABC.由基本事实3可知点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上,∴P,Q,R三点共线.
(方法二)∵AP∩AQ=A,∴直线AP与直线AQ确定平面APQ.又AB∩α=P,AC∩α=Q,∴平面APQ∩α=PQ.∵B∈平面APQ,C∈平面APQ,∴BC⊂平面APQ.∵R∈BC,∴R∈平面APQ,又R∈α,∴R∈PQ,∴P,Q,R三点共线.
命题角度3 证明线共点例3　如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AA1的中点,求证:(1)E,C,D1,F四点共面;(2)CE,D1F,DA三线共点.
证明 (1)如图,连接EF,CD1,A1B.∵E,F分别是AB,AA1的中点,∴EF∥A1B.又A1B∥CD1,∴EF∥CD1,∴E,C,D1,F四点共面.(2)∵EF∥CD1,EF