高端精品高中数学一轮专题-导数综合检测卷4试卷

这是一份高端精品高中数学一轮专题-导数综合检测卷4试卷，共6页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
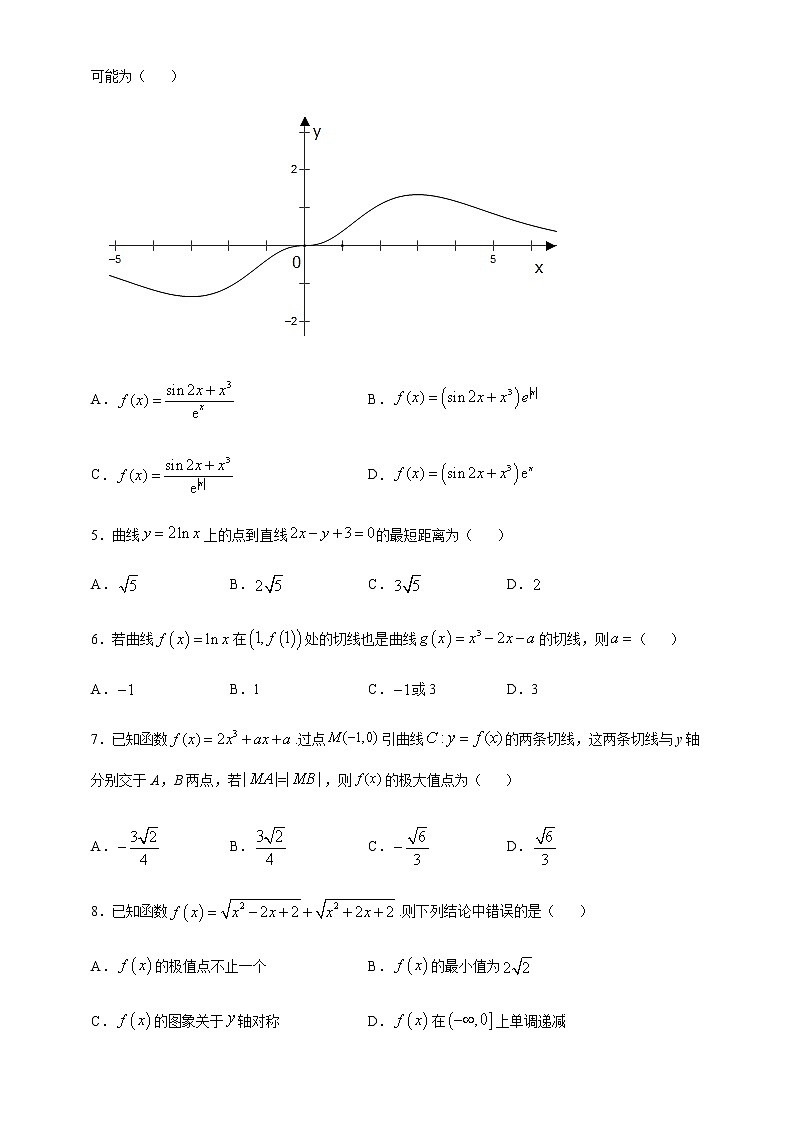
导数综合检测卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知函数的图象如图所示，下面四个图象中的图象大致是 （  ） A． B．C． D．2．若函数，则与的大小关系是（    ）A． B．C． D．不确定3．设直线与函数，的图象分别交于点，，则当达到最小时的值为（    ）A．1 B． C． D．4．著名数学家华罗庚先生曾说过：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休.”在数学的学习和研究中，经常用函数的图象来研究函数的性质，也经常用函数的解析式来琢磨函数的图象的特征，已知函数，的部分图像如图所示 ，则的解析式可能为（    ）A． B．C． D．5．曲线上的点到直线的最短距离为（    ）A． B． C． D．6．若曲线在处的切线也是曲线的切线，则（    ）A． B．1 C．或3 D．37．已知函数.过点引曲线的两条切线，这两条切线与y轴分别交于A，B两点，若，则的极大值点为（    ）A． B． C． D．8．已知函数.则下列结论中错误的是（    ）A．的极值点不止一个 B．的最小值为C．的图象关于轴对称 D．在上单调递减二、多选题9．函数在定义域R内可导，若，且，若，则a，b，c的大小关系正确的有（    ）A． B． C． D．10．已知函数有两个互异的极值点，下列说话正确的是（    ）A．B．有三个零点的充要条件是C．时，在区间上单调递减D．时，为极大值，为极小值11．若存在，使得对任意恒成立，则函数在上有下界，其中为函数的一个下界；若存在，使得对任意恒成立，则函数在上有上界，其中为函数的一个上界.如果一个函数既有上界又有下界，那么称该函数有界.下列说法正确的是（    ）A．2是函数的一个下界 B．函数有下界，无上界C．函数有上界，无下界 D．函数有界12．如图，在四面体中，点，，分别在棱，，上，且平面平面，为内一点，记三棱锥的体积为，设，对于函数，则下列结论正确的是（    ）A．当时，函数取到最大值B．函数在上是减函数C．函数的图象关于直线对称D．不存在，使得(其中为四面体的体积).三、填空题13．设存在导函数且满足，则曲线上的点处的切线的斜率为______________.14．在中，分别为角的对边，若函数有极值点，则的范围是__________．15．对于三次函数，给出定义：设是函数的导数，是的导数，若方程=0有实数解，则称点(，)为函数的“拐点”.经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.设函数，则=__________.16．如图，在矩形与扇形拼接而成的平面图形中，，，，点在弧上，在上，.设，则当平面区域（阴影部分）的面积取到最大值时__________ 四、解答题17．已知二次函数.（1）求在点处的切线方程；（2）讨论函数的单调性18．如图，某市地铁施工队在自点M向点N直线掘进的过程中，因发现一地下古城(如图中正方形所示区域)而被迫改道.原定的改道计划为：以M点向南，N点向西的交汇点为圆心，为半径做圆弧，将作为新的线路，但由于弧线施工难度大，于是又决定自点起，改为直道.已知千米，点A到OM，ON的距离分别为千米和1千米，，且千米，记.（1）求的取值范围；（2）已知弧形线路的造价与弧长成正比，比例系数为3a，直道PN的造价与长度的平方成正比，比例系数为a，当θ为多少时，总造价最少？19．已知函数（1）若存在极值点1，求的值；（2）若存在两个不同的零点，求证：20．已知函数.（1）讨论函数的单调性；（2）若存在两个极值点，求证：.21．已知函数.（1）求函数的单调区间；（2）若不等式恒成立，求实数的取值范围；（3）当时，求证：.22．已知函数，为的导函数.（1）若，恒成立，求的取值范围；（2）证明：函数在上存在唯一零点.