高端精品高中数学一轮专题-极值与最值3试卷

这是一份高端精品高中数学一轮专题-极值与最值3试卷，共5页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
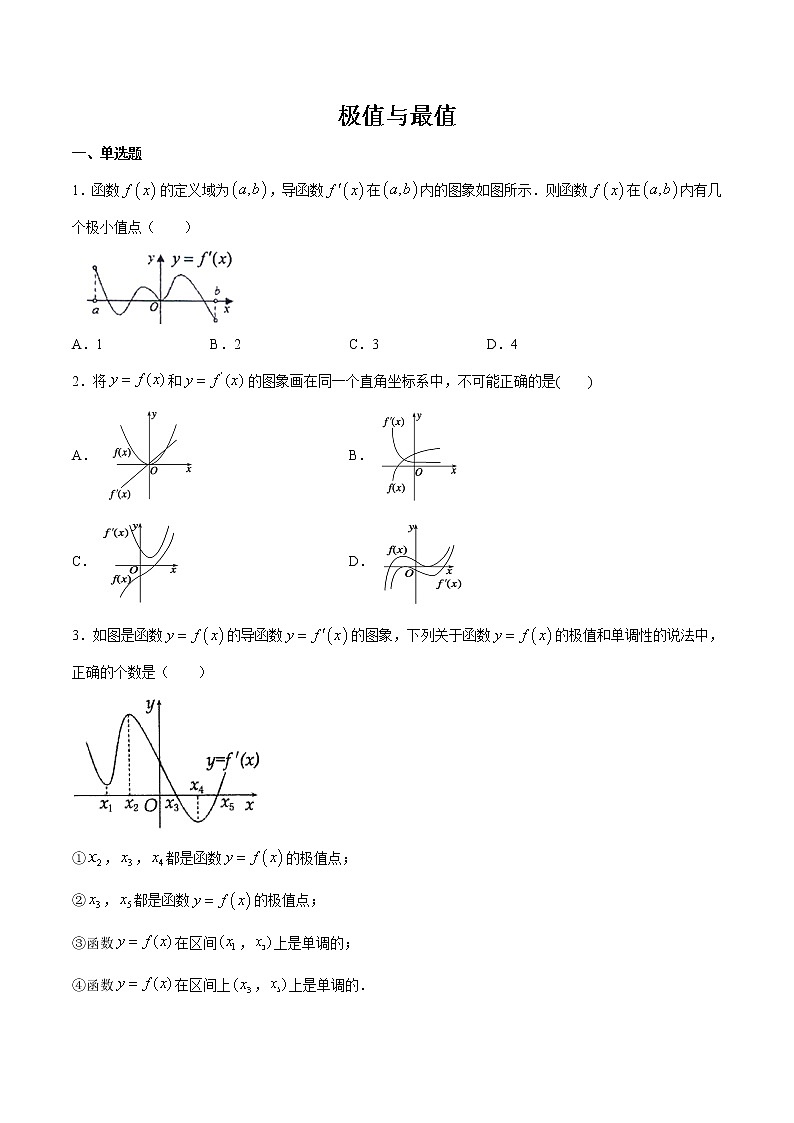
极值与最值一、单选题1．函数的定义域为，导函数在内的图象如图所示．则函数在内有几个极小值点（    ）A．1 B．2 C．3 D．42．将和的图象画在同一个直角坐标系中，不可能正确的是(    )A． B．C． D．3．如图是函数的导函数的图象，下列关于函数的极值和单调性的说法中，正确的个数是（    ）①，，都是函数的极值点；②，都是函数的极值点；③函数在区间，上是单调的；④函数在区间上，上是单调的．A．1 B．2 C．3 D．44．如图是函数的导数的图象，则下面判断正确的是（    ）A．在内是增函数B．在时取得极大值C．在内是增函数D．在时取得极小值5．已知函数在处取得极大值，则c的值为（    ）A．2 B．6 C．4 D．6．已知函数在处有极值10，则等于(   )A．1 B．2 C．—2 D．—17．已知函数，，若，，则的大小为（    ）A． B． C． D．8.若函数在上是单调函数，则a的取值范围是（    ）A． B．C． D．二、多选题9．定义在上的可导函数的导函数的图象如图所示，以下结论正确的是（    ）A．-3是的一个极小值点；B．-2和-1都是的极大值点；C．的单调递增区间是；D．的单调递减区间是．10．已知函数的导函数的图象如图所示，那么下列图象中不可能是函数的图象的是（    ）A． B．C． D．11．已知函数的定义域为，则（    ）A．为奇函数B．在上单调递增C．恰有4个极大值点D．有且仅有4个极值点12．若函数在定义域上单调递增，则称函数具有性质.下列函数中所有具有性质的函数为（    ）.A． B． C． D．三、填空题13．函数的极小值为_______________．14．已知函数的图象如图所示，则不等式的解集为______．15．如图是的导函数的图象，现有四种说法．（1）在上是增函数，（2）是的极小值点（3） 在上是增函数，（4）是的极小值点以上说法正确的序号是_________16．若函数在区间单调递增，则的取值范围是______；若函数在区间内不单调，则的取值范围是______.四、解答题17．已知函数．（1）求曲线在点处的切线方程；（2）求函数的极值．18．已知函数.（1）当时，求曲线在点处的切线方程；（2）求的单调区间；19．已知函数在处有极值．（1）求a,b的值；（2）求的单调区间．20．已知函数在与时都取得极值.（1）求，的值；（2）求函数的单调区间，并指出与是极大值还是极小值.21．已知函数f（x）＝ax3+bx2﹣3x在x＝﹣1和x＝3处取得极值.（1）求a，b的值（2）求f（x）在[﹣4，4]内的最值.22．已知函数（1）求函数的极值（2）求函数在区间上的最值．