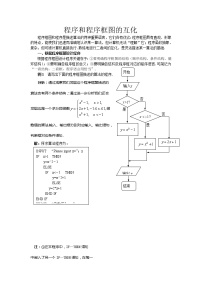
2020-2021学年2.4.2空间两点的距离公式教学设计
展开巧思妙想 坐标来帮忙
有些立体几何问题转化为平面几何问题后对逻辑推理能力的要求也比较高,而且有时容易出错,这时若能换个角度,用解析几何知识来解决,则往往思路清晰、简捷明了.
用坐标法解题,需要分析清楚对象的几何关系,有时需要根据题设条件构造某一几何关系,然后在适当的坐标系下通过运算才能加以解决.
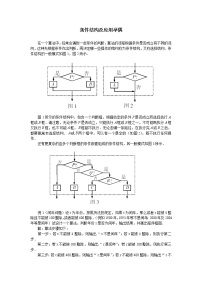
例1 如图1,已知在直三棱柱中,,,,,是的中点.求证:.
解析:由题设可得平面,连结,则是在平面上的射影,因此只需证明就行了,将平面分离出来,如图2,建立直角坐标系.由已知可得,,,.
又∵,,,∴.∴.
例2 在正方体中,为的中点,求截面和截面所成二面角的度数.
解析:如图3,连结,交于点,连结,可知,是所求二面角的平面角,在平面中,如图4,建立直角坐标系,设,则,,,.
∴.
∴.
∴.
∴所求二面角的度数为90°.
例3 如图5,已知平行六面体的底面是菱形,且.
(1)证明:;
(2)假设,,记平面为,平面为,求二面角的平面角的余弦值;
(3)当的值为多少时,能使平面?请给出证明.
解析:(1),(2)略.
(3)由(1)知.
又∵,
∴平面.
∴.
要使平面,
则需,又在平面上的射影为(为的交点),从而需证.
在平面上建立直角坐标系,如图6,设,,易求出各点的坐标为,,,,
由,得,
∴,
整理得.
∴或(舍去).
∴.
例4 已知在正三棱柱中,,,求线段在侧面上的射影长.
解析:如图7,取面为参照面,过点作于点.
连结,由,知,,.
设,以,线段所在直线为坐标轴,建立如图所示坐标系,
则(1,0),(2,0),(2,),(0,).
由,得,
解得,故.
高中数学人教版新课标B必修22.4.2空间两点的距离公式教案设计: 这是一份高中数学人教版新课标B必修22.4.2空间两点的距离公式教案设计,共4页。教案主要包含了利用线面垂直关系建系,利用面面垂直关系建系等内容,欢迎下载使用。
数学必修22.4.2空间两点的距离公式教学设计: 这是一份数学必修22.4.2空间两点的距离公式教学设计,共1页。
高中数学人教版新课标B必修22.4.2空间两点的距离公式教案设计: 这是一份高中数学人教版新课标B必修22.4.2空间两点的距离公式教案设计,共2页。