数学必修22.3.1圆的标准方程教案

这是一份数学必修22.3.1圆的标准方程教案，共20页。PPT课件主要包含了则PA⊥PB，轨迹法，待定系数法，圆心两条直线的交点，半径圆心到圆上一点，A11，B2-2，弦AB的垂直平分线，公式法等内容，欢迎下载使用。

(1) 求到点C(1, 2)距离为2的点的轨迹方程.
∴ (x 1)2 + ( y  2)2 = 4
(2) 方程(x 1)2 + ( y  2)2 = 4表示的曲线是什么？
以点C(1, 2)为圆心， 2为半径的圆.
知识探究一：圆的标准方程
设圆上任意一点P(x,y),
平面内与定点的距离等于定长的点的集合(轨迹)叫做圆.
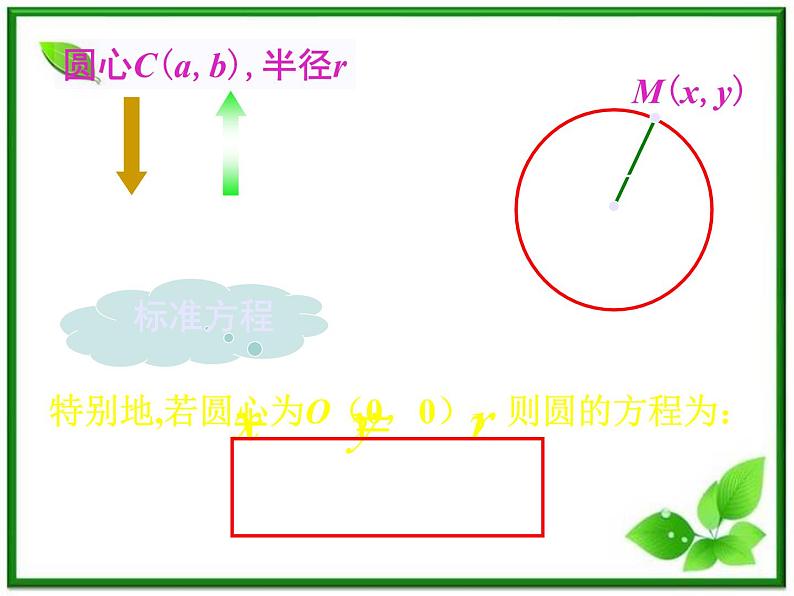
圆心为C(a, b), 半径为r的圆的标准方程.
(x  a)2 + ( y  b)2 = r2
圆心C(a,b),半径r
特别地,若圆心为O（0，0），则圆的方程为：
3. 特殊位置的圆的方程:
x2 + y2 = r2 (r≠0)
(x  a)2 + y2 = r2 (r≠0)
x2+ (y  b)2 = r2 (r≠0)
(x  a)2 + (y-b)2 = b2 (b≠0)
圆心在x轴上且过原点:
(x  a)2 + y2 = a2 (a≠0)
圆心在y轴上且过原点:
x 2 + (y-b)2 = b2 (b≠0)
(x  a)2 + (y-b)2 = a2+b2 (a2+b2≠0)
(x  a)2 + (y-b)2 = a2 (a≠0)
圆与x,y轴都相切:
(x  a)2 + (y±a)2 = a2 (a≠0)
1.说出下列圆的方程： (1) 圆心在原点,半径为3. (2) 圆心在点C(3, -4), 半径为7.
2. 说出下列方程所表示的圆的圆心坐标和半径：
(1) (x + 7)2 + ( y  4)2 = 36
(2) x2 + y2  4x + 10y + 28 = 0
x 2 + y 2 =9
圆心C( 7, 4), r = 6
圆心C(2， 5), r = 1
圆心C(a, 0), r = |m|
(3) (x  a)2 + y 2 = m2
(x  3)2 +( y+4) 2 = 49
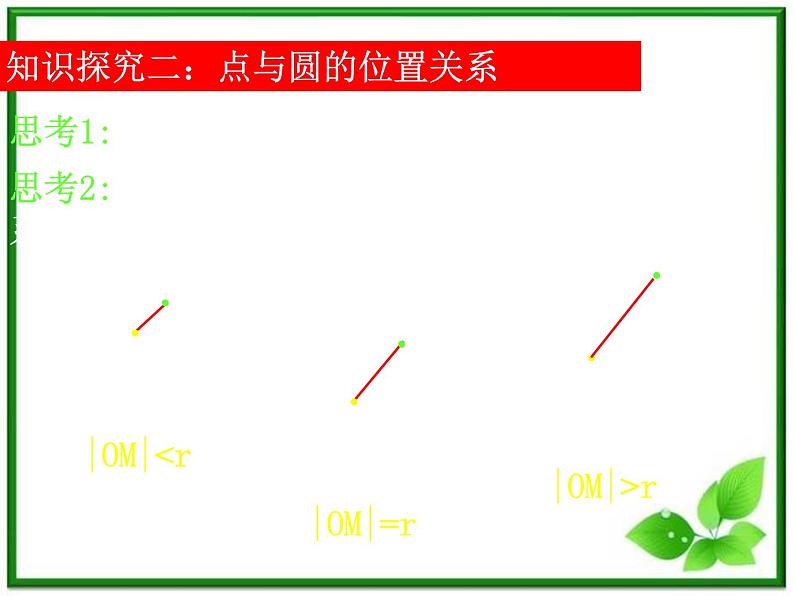
知识探究二：点与圆的位置关系
思考1:在平面几何中,点与圆有哪几种位置关系？
思考2:在平面几何中，如何确定点与圆的位置关系？
思考3:在直角坐标系中，已知点M(x0，y0)和圆C： ，如何判断点M在圆外、圆上、圆内？
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2思考4:经过三个不共线的点分别可以作多少个圆？
思考5:集合{(x，y)|(x-a)2+(y-b)2≤r2}表示的图形是什么？
不等式表示：(x-a)2+(y-b)2=r2的圆及其内部
不共线的三个点确定唯一一个圆
由公式得圆的标准方程为：
例1已知两点P1(4, 9)和P2(6, 3)，求以P1P2为直径的圆的方程.
5.圆的方程的求法:
①公式法:求出圆心，半径，代入圆方程
(x  5)2 + ( y  6)2 = 10
步骤1:设出圆的方程
步骤3:写出圆的方程
思考:一般地，已知点A(x1，y1)，B(x2，y2)，则以线段AB为直径的圆方程如何？
(x-x1)(x-x2)+(y-y1)(y-y2)=0
设圆上任意一点P(x,y),
解：设所求圆的方程为：
因为A(5,1),B (7,-3),C(2,8)都在圆上
例2 ⊿ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求它的外接圆的方程.
例3.己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
解:∵A(1,1),B(2,-2)
∴圆心C(-3,-2)
圆经过A(1,1),B(2,-2)
∵圆心在直线l:x-y+1=0上
例5.求以(1，3)为圆心，并且和直线 3x-4y-7=0相切的圆的方程.
分析：要确定圆的方程需要几个独立条件?已经知道几个条件？还需要什么条件？
解:∵圆心C(1，3),
圆C和直线3x-4y-7=0相切,
∴半径ｒ等于圆心C到直线3x-4y-7=0的距离.
由点到直线的距离公式,得:
2 .求满足下列条件的圆的方程：
1.点(2a, 1  a)在圆x2 + y2 = 4的内部,求实数 a 的取值范围.
(x  6)2 + y2 = 25或(x + 2)2 + y2 = 25
 < a < 1
(1) 圆心在 x 轴上,半径为5,且过点A(2, 3).
(2)过点A(3,1)和B( 1，3),且圆心在直线3x-y-2=0上.
(x  2)2 + ( y  4)2 = 10
(3)求以点C(1，3)为圆心,并且和直线3x-4y-7=0相切的圆的方程.
(x  1)2 + ( y  3)2 =
3.求满足下列条件的圆的方程：
(x + 2)2 + y2 = 50
x2 + ( y  6)2 = 10
(x  8)2 + ( y + 3)2 = 25
(1) 经过点A(3,5)和B(3,7),并且圆心在 x 轴上.
(2) 经过点A(3,5)和B(3,7),并且圆心在 y 轴上.
(3) 经过点P(5,1),且圆心在C(8, 3).
(4)求圆心C在直线 x+2y+4=0 上,且过两定点A(1,1), B(1,-1)的圆的方程。