高中数学2.3.3直线与圆的位置关系教案设计

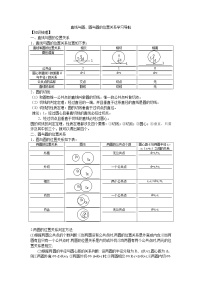
这是一份高中数学2.3.3直线与圆的位置关系教案设计，共2页。教案主要包含了复习准备，讲授新课，巩固练习等内容，欢迎下载使用。
学习要求：能根据给定圆的方程，判断圆与圆的位置关系；
学习重点：能根据给定圆的方程，判断圆与圆的位置关系
学习难点：用坐标法判断两圆的位置关系
学习过程：
一、复习准备
1． 两圆的位置关系有哪几？
2．设两圆的圆心距为d.
当时，两圆 ， 当时，两圆
当 时，两圆 ，当时，两圆
当时，两圆
３．如何根据圆的方程，判断两圆之间的位置关系？(探讨)
二、讲授新课：
1.两圆的位置关系利用半径与圆心距之间的关系来判断
已知圆，圆，试判断圆与圆的关系？
方法（一）（配方→圆心与半径→探究圆心距与两半径的关系）
方法（二）解方程组
探究：相交两圆公共弦所在直线的方程。
两圆的位置关系利用圆的方程来判断
方法：通常是通过解方程或不等式和方法加以解决 （以例1为例说明）
例2．圆的方程是:圆的方程是: ,
m为何值时,两圆(1)相切.(2)相交(3)相离(4)内含
思路：联立方程组→讨论方程的解的情况（消元法、判别式法）→交点个数→位置关系）
练习：已知两圆与，问m取何值时，两圆相切。
例3．已知两圆和圆的交点为A、B,
（1）求AB的长； （2）求过A、B两点且圆心在直线上的圆的方程.
3.小结：判断两圆的位置关系的方法:
(1)由两圆的方程组成的方程组有几组实数解确定.
(2)依据连心线的长与两半径长的和或两半径的差的绝对值的大小关系.
三、巩固练习：
1．求经过点M(2,-2),且与圆与交点的圆的方程
2．已知圆C与圆相外切,并且与直线相切于点,求圆C的方程.
3．求两圆和的外公切线方程