人教版新课标B1.2.3空间中的垂直关系导学案

这是一份人教版新课标B1.2.3空间中的垂直关系导学案，共23页。PPT课件主要包含了情境引入，图形语言，符号语言，数学理论，已知点Aa，存在性，因为B∈C∈，唯一性，数学运用，证法一等内容，欢迎下载使用。
1.你是怎样来认识一个平面的?怎样 来表示一个平面?它的记法是什么?
2.空间中的点,线,面之间的位置关系 是怎样用符号来表示的?
问题1：为什么当一个人在学会走路之前总会有一段爬行的人生经历，同时也有一段拄着拐杖的人生历程？在爬行与拄拐杖这两件事情中是否隐含着什么数学理论呢？
问题2：用两个合页和一把锁就可以固定一扇门，为什么？
问题3：自行车的撑脚一般安装在自行车的什么位置？能不能安装在前后轮一条直线的地方 ？
问题4：照相机支架需要几条腿？两条行不行？三条在一条线上行不行？
根据上面的实例，你得到怎么样的一个结论？如何用数学语言描述上述事实？
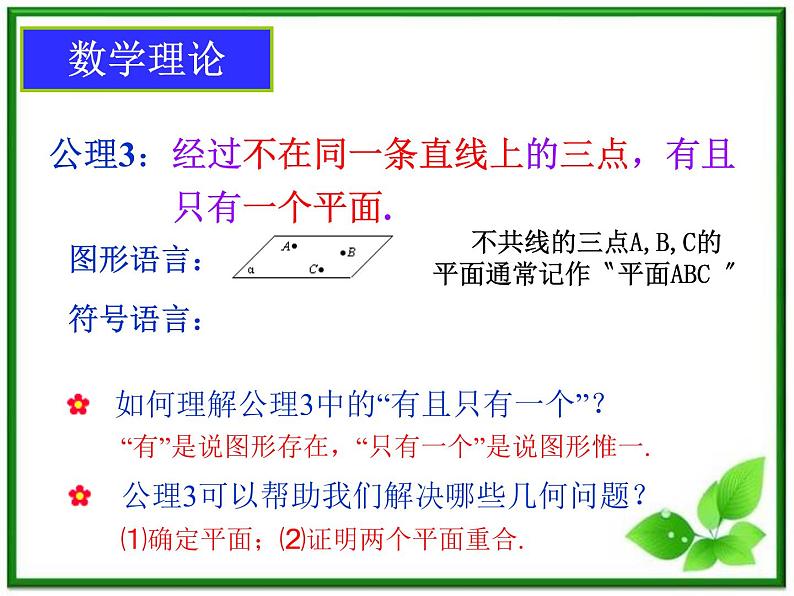
公理3：经过不在同一条直线上的三点，有且 只有一个平面.
如何理解公理3中的“有且只有一个”？
“有”是说图形存在，“只有一个”是说图形惟一.
公理3可以帮助我们解决哪些几何问题？
⑴确定平面；⑵证明两个平面重合.
不共线的三点A,B,C的平面通常记作〝平面ABC 〞
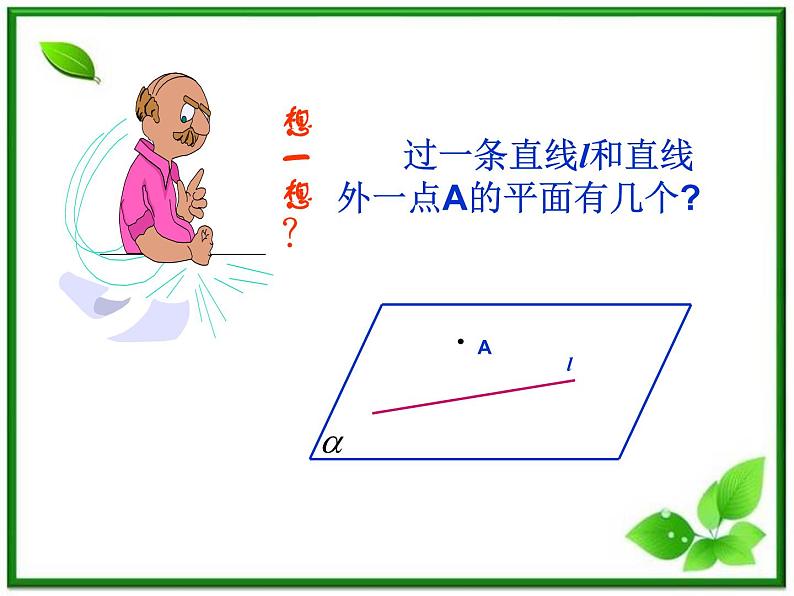
过一条直线l和直线外一点A的平面有几个?
推论1：经过一条直线和这条直线外的一点有 且只有一个平面.
　　分析：先在直线l上任取两点Ｂ,Ｃ，这样Ａ,Ｂ,Ｃ三点就能确定一个平面，再证明l在这个平面内．
推论1  经过一条直线和这条直线外一点,有且只有一个平面.
求证：过点A和直线a可以确定一个平面.
因为A a，在a上任取两点B，C.
所以过不共线的三点A，B，C有一个平面.（公理3）
所以a∈.（公理1）
故经过点A和直线a有一个平面.
如果经过点A和直线a的平面还有一个平面，那么A∈，a  
因为B∈a， C∈a，所以B∈，C∈β.（公理1）
故不共线的三点A，B，C既在平面内又在平面内.所以平面和平面重合.（公理3）
所以经过点A和直线a有且只有一个平面 .
即直线AD、BD、CD共面．
推论2：经过两条相交直线，有且只有一个 平面.
推论2：经过两条相交直线有且只有一个平面.
在a上取不同于点P的点A．
即：过 a，b 有且只有一个平面．
　　右图是一张倒置的课桌，你能用所学的知识检查一下桌子的四条腿是否在同一个平面内？
【例2】两两相交且不共点 的三条直线必在同 一个平面内.
已知：AB∩AC=A，AB∩BC=B，AC∩BC=C
求证：直线AB，BC，AC共面.
所以直线AB，AC确定一个平面.（推论2）
因为B∈AB，C∈AC，所以B∈，C∈，
故BC.（公理1）
因此直线AB，BC，CA共面.
因为A 直线BC上，
所以过点A和直线BC确定平面.（推论1）
因为A∈， B∈BC，所以B∈.
故AB  ，同理AC  ，
所以AB，AC，BC共面.
因为A，B，C三点不在一条直线上，
所以过A，B，C三点可以确定平面.（公理3）
因为A∈，B∈，所以AB  .（公理1）
同理BC  ，AC  ，
所以AB，BC，CA三直线共面.
要证各线共面，先确定一个平面，再证明其他直线也在这个平面内．
推论3：经过两条平行的直线有且只有一个 平面.
推论3：经过两条平行的直线有且只有一个平面.
设点A为直线a上任一点
又由推论1，过点A和直线b的平面只有一个
【例3】一条直线和三条平行线都相交, 求证这四条直线共面.
已知：a∥b∥c , a∩l = A, b∩l = B ,c∩l = C．求证：a, b ,c , l共面．
有二位同学证明如下，请判断正误：
又∵a∩l=A,b∩l=B,
∴a, b, c, l共面.
∵经过两条相交直线有且只有一个平面.
2.如图,平面 , , ,且 = a, = b, = c, a b = A. 求证: A ∈ c .
1．平面的基本性质(公理与推论）．
2．三个推论的应用（共点、共线、 共面问题）．