高中人教版新课标B1.2.3空间中的垂直关系学案
展开课 题 | 空间中的平行关系
| 课型 | 新课 |
| ||||
主备人 |
| 上课教师 |
| 上课时间 | 45 分钟 | |||
学习目标 | 以所学过的作为推理依据的一些公理和定理为基础,通过直观感知,操作确认,思辨论证,归纳出空间中线、面平行的有关判定定理和性质定理。能运用已获得的结论证明一些空间位置关系的简单命题。 | |||||||
教学重点 | 平面的基本性质与推论以及它们的应用;线线平行及平行线的传递性和面面平行的定义与判定。 | |||||||
教学难点 | 自然语言与数学图形语言和符号语言间的相互转化与应用;如何由平行公理以及其他基本性质推出空间线、线,线、面和面、面平行的判定和性质定理,并掌握这些定理的应用。 | |||||||
教师准备 | 多媒体教学 | |||||||
教学过程 | 集备修正 | |||||||
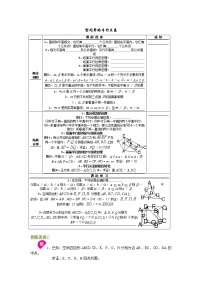
(二)平面中的平行关系 1. 平行直线 (1)空间两条直线的位置关系 ①相交:在同一平面内,有且只有一个公共点; ②平行:在同一平面内,没有公共点。 (2)初中几何中的平行公理: 过直线外一点有且只有一条直线和这条直线平行。 【说明】此结论在空间中仍成立. (3)公理4(空间平行线的传递性): 平行于同一条直线的两条直线互相平行.即:如果直线a // b,c // b,那么a // c。 【说明】此公理是判定两直线平行的重要方法:寻找第三条直线分别与前两条直线平行。 2. 等角定理 等角定理:如果一个角的两边和另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。 需要说明的是:对于等角定理中的条件:“方向相同”。 (1)若仅将它改成“方向相反”,则这两个角也相等。 (2)若仅将它改成“一边方向相同,而另一边方向相反”,则这两个角互补。此定理及推论是证明角相等问题的常用方法。 3. 空间图形的平移 如果空间图形F的所有点都沿同一方向移动相同的距离到F'的位置,则说图形F在空间做了一次平移。 注意:图形平移后与原图形全等,即对应角和对应两点间的距离保持不变。 图形平移有如下性质: (1)平移前后的两个图形全等; (2)对应角的大小平移前后不变; (3)对应两点的距离平移前后不变; (4)对应两平行直线的位置关系在平移前后不变; (5)对应两垂直直线的位置关系在平移前后不变。 4. 证明空间两直线平行的方法 (1)利用定义 用定义证明两条直线平行,需证两件事:一是两直线在同一平面内;二是两直线没有公共点。 (2)利用公理4 用公理4证明两条直线平行,只需证一件事:就是需找到直线c,使得a // c,同时b//c,由公理4得a // b。 例1. 已知四面体ABCD中,M、N分别是和的重心。 求证:(1)面ABD;(2)面CMN 分析:首先根据条件画出图形,如图所示,证明线面平行最常用的方法是利用判定定理,利用反推的思想,要证面ABD,只要证明MN平行于面ABD内的某一条直线即可。根据M、N分别为的重心的条件,连接CM、CN并延长分别交AB、AD于G、H,连接GH。若有,则结论可证,或连接AM、AN并延长交BC、CD于E、F,连接EF,若有,,结论可证。 解析:(1)如图所示,连接CM、CN并延长分别交AB、AD于G、H,连接GH、MN ∵M、N分别为的重心
∴MN∥GH 又面ABD,面ABD ∴MN∥面ABD (2)连接AM、AN并延长分别交BC、CD于E、F,连结EF 同理MN∥EF 又E、F分别为BC、CD的中点 ∴BD∥EF ∴BD∥MN 又面CMN,CMN ∴BD∥面CMN 点评:证明线面平行的常用方法有两种,其一是利用定义,一般借助反证法去完成;其二是利用判定定理,思路一般是从结论入手,用反推的思想方法分析出解题思路,然后完成证明过程。 |
| |||||||
作业 |
| |||||||
板书 |
| |||||||
课后反思 |
| |||||||
数学必修21.2.3空间中的垂直关系导学案: 这是一份数学必修21.2.3空间中的垂直关系导学案,共5页。学案主要包含了典型例题等内容,欢迎下载使用。
人教版新课标B必修21.2.3空间中的垂直关系学案: 这是一份人教版新课标B必修21.2.3空间中的垂直关系学案,共5页。学案主要包含了知识结构,重点,教法建议,例题解析,练习,小结等内容,欢迎下载使用。
数学必修21.2.3空间中的垂直关系学案设计: 这是一份数学必修21.2.3空间中的垂直关系学案设计,共3页。学案主要包含了教学目标,引入,教学过程,例题解析,练习,小结等内容,欢迎下载使用。