高中数学人教版新课标B必修21.2.3空间中的垂直关系学案
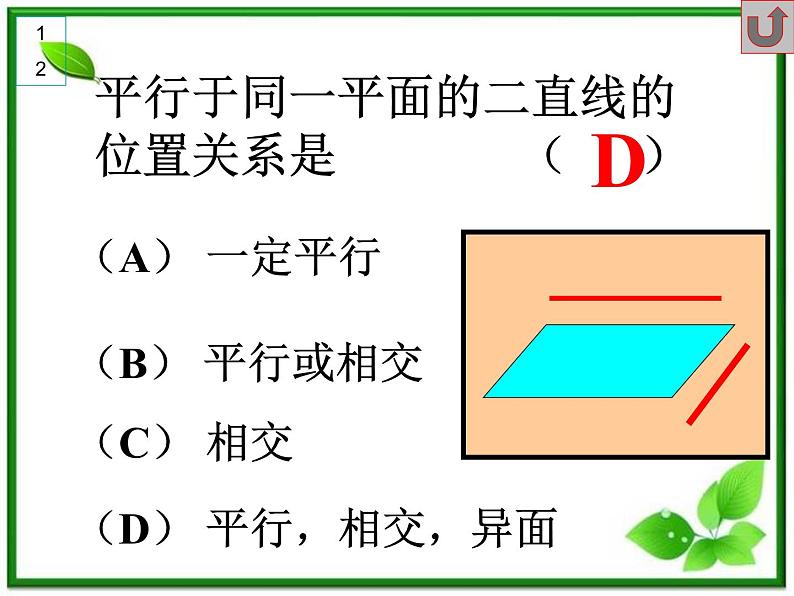
展开平行于同一平面的二直线的位置关系是 ( )
(D) 平行,相交,异面
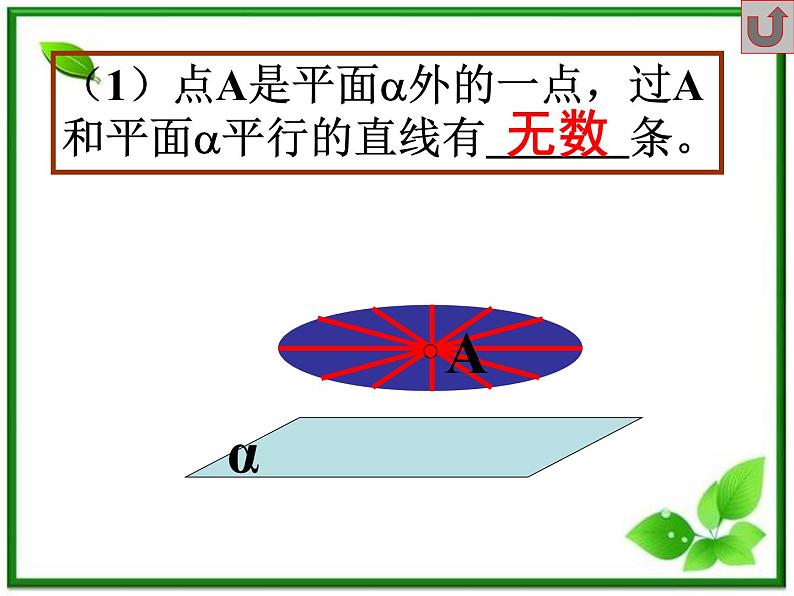
(1)点A是平面外的一点,过A和平面平行的直线有 条。
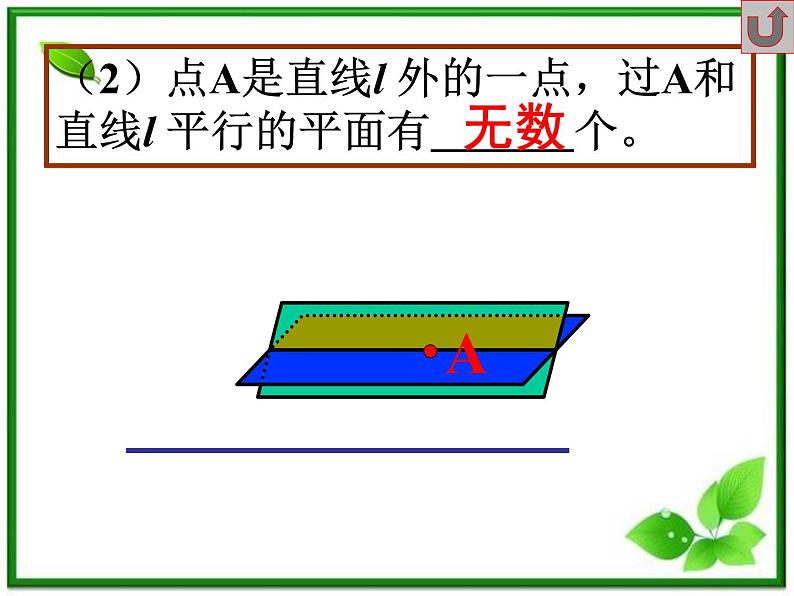
(2)点A是直线l 外的一点,过A和直线l 平行的平面有 个。
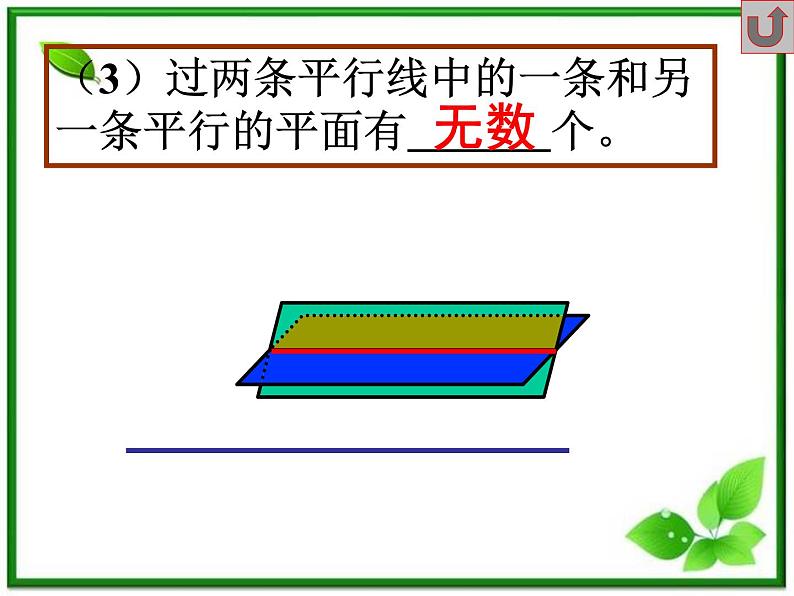
(3)过两条平行线中的一条和另一条平行的平面有 个。
(4)过两条异面直线中的一条和另一条平行的平面有 个。
(5)如果l1 // l2 , l1 平行于平面, 则l2 平面
(6)如果两直线a ,b 相交,a平行于平面,则b与平面的位置关系是 。
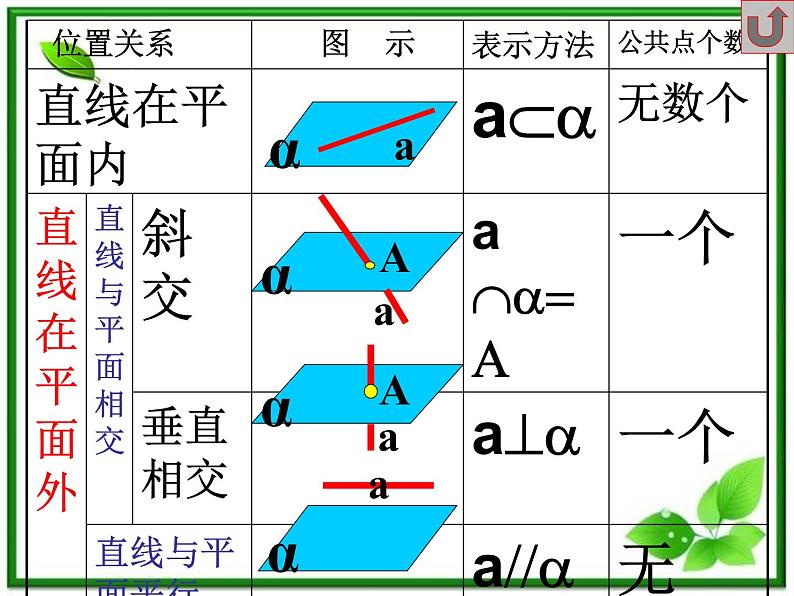
(1) 定义——直线与平面没有公共点
(2) 定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
已知:a b a//b
(1) a,b确定平面,=b
(2) 假设a与不平行
(3) 这与已知a//b矛盾
(4) ∴a //
如图,空间四面体P-ABC, M,N分别是面PCA和面PBC的重心 求证:MN//面BCA
∴ MN //面BCA
如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCE
∴ MN //面BCE
∵△AFN∽ △BNH
∴ AN/NH=FN/BN
∴ AN/NH=AM/MC
在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1E
∴ DB1 //面A1C1E
在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1B
(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点
(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线
(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。
已知:a//,a, =b
如果平面外的两条平行线中的一条与这个平面平行,则另一条直线与这个平面也平行
如果一条直线和两个相交平面都平行,则这条直线与它们的交线平行
已知:a // , a// , =l
如图,a,b是异面直线,O为AB的中点,过点O作平面与两异面直线a,b都平行MN交平面于点P,求证:MP=PN
一、两个平面平行的判定方法
1、两个平面没有公共点
2、一个平面内有两条相交 直线都平行于另一个平面
3、都垂直于同一条直线的 两个平面
二、两个平面平行的性质
判断下列命题是否正确?
1、平行于同一直线的两平面平行
2、垂直于同一直线的两平面平行
3、与同一直线成等角的两平面平行
4、垂直于同一平面的两平面平行
5、若α∥β,则平面α内任一直线a ∥β
例题、如图,在正方体ABCD-A1B1C1D1 中,求证:面AB1D1∥面BDC1
B1D1∩AB1=B1
面AB1D1∥面BDC1
变形1:如图,在正方体ABCD-A1B1C1D1 中,E,F,G分别为A1D1, A1B1, A1A的中点求证:面EFG∥面BDC1
变形2:若O为BD上的点求证:OC1 ∥面EFG
由上知面EFG∥面BDC1
变形3:如图,在正方体ABCD-A1B1C1D1 中,E,F,M,N分别为A1B1, A1D1, B1C1, C1D1 的中点
求证:面AEF∥面BDMN
2021学年1.2.3空间中的垂直关系学案设计: 这是一份2021学年1.2.3空间中的垂直关系学案设计,共17页。PPT课件主要包含了一平行直线,公理4的符号表述为,线∥线,线∥面,面∥面等内容,欢迎下载使用。
人教版新课标B必修21.2.3空间中的垂直关系导学案及答案: 这是一份人教版新课标B必修21.2.3空间中的垂直关系导学案及答案,共4页。学案主要包含了复习知识,基础训练,典例精析,归纳小结等内容,欢迎下载使用。
数学1.2.3空间中的垂直关系导学案: 这是一份数学1.2.3空间中的垂直关系导学案,共11页。学案主要包含了课标要求,命题走向,要点精讲,典例解析,命题立意,思维总结等内容,欢迎下载使用。