数学7.3等比数列导学案

这是一份数学7.3等比数列导学案，共4页。学案主要包含了教学内容分析，教学目标设计，教学重点及难点，教学用具准备，教学流程设计，教学过程设计，教学设计思想等内容，欢迎下载使用。
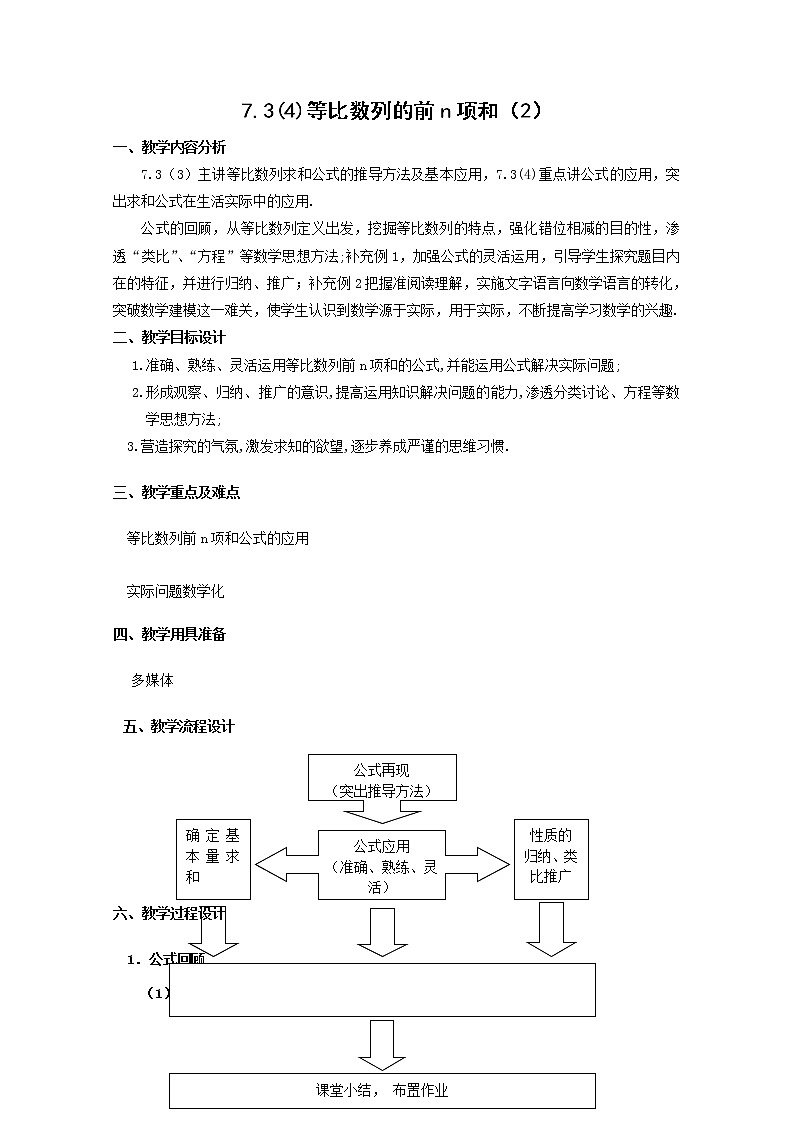
7.3(4)等比数列的前n项和（2）一、教学内容分析7.3（3）主讲等比数列求和公式的推导方法及基本应用，7.3(4)重点讲公式的应用，突出求和公式在生活实际中的应用.公式的回顾，从等比数列定义出发，挖掘等比数列的特点，强化错位相减的目的性，渗透“类比”、“方程”等数学思想方法;补充例1，加强公式的灵活运用，引导学生探究题目内在的特征，并进行归纳、推广；补充例2把握准阅读理解，实施文字语言向数学语言的转化，突破数学建模这一难关，使学生认识到数学源于实际，用于实际，不断提高学习数学的兴趣.二、教学目标设计1.准确、熟练、灵活运用等比数列前n项和的公式,并能运用公式解决实际问题;2.形成观察、归纳、推广的意识,提高运用知识解决问题的能力,渗透分类讨论、方程等数学思想方法;3.营造探究的气氛,激发求知的欲望,逐步养成严谨的思维习惯.三、教学重点及难点等比数列前n项和公式的应用实际问题数学化四、教学用具准备多媒体五、教学流程设计 六、教学过程设计1．公式回顾（1）等比数列前n项公式推导方法①     错位相减(突出错项相减的目的性)②     方程思想 (突出构造方程的思想)③     定义出发运用等比定理(突出转化思想)(2)公式的再认识      ①公式的形式(分类思想)②公式的应用(方程思想)(3)巩固练习①求和 (突出项数变化)②求和 (培养观察的意识,突出分类思想)2.公式应用例1.已知等比数列中, ,求.设问1:能否根据条件求和q ？ 如何求？ 一定要求q吗？(基本量的确定)设问2:等比数列中每隔4项的和组成什么数列？ (探究等比数列内在的联系)设问3:若题变: 数列是等比数列,且求引导学生归纳:若是等比数列,公比为q,则每隔n项的和组成一个首项为,公比为的等比数列.(学生类比等差数列相关结论)[说明]解题首先考虑的是通法,先确定基本量然后再求和，其次分析题目的特点、内在结构,探索规律,并从特殊向一般推广，注意培养学生思维的严谨性.例2.某商店采用分期付款的方式促销一款价格每台为6000元的电脑.商店规定，购买时先支付货款的，剩余部分在三年内按每月底等额还款的方式支付欠款，且结算欠款的利息.已知欠款的月利率为0.5%（1）       到第一个月底，货主在第一次还款之前，他欠商店多少元？（2）       假设货主每月还商店元，写出在第i(i=1,2,36)个月末还款后，货主对商店欠款数的表达式.（3）       每月的还款额为多少元（精确到0.01）？引导学生,认真阅读题目,理解题意,月底等额还款,即每月末还款数一样，第i个月底还款后的欠款数与第i-1个月底还款后的欠款数的关系是,(学生分析)三年内还清转化为数学语言是: 解(1)因为购买电脑时,货主欠商店的货款,即6000=4000(元),又按月利率0.5%到第一个月底的欠款数应为4000(1+0.5%)=4020(元).即到第一个月底,欠款余额为4020元.   (2)设第i个月底还款后的欠款数为y,则有    y=4000(1+0.5%)-   y=y(1+0.5%)-     =4000(1+0.5%)-(1+0.5%)-   y=y(1+0.5%)-     =4000(1+0.5%)-(1+0.5%)-(1+0.5%)-                       y=y(1+0.5%)-=4000(1+0.5%)-(1+0.5%)-(1+0.5%)- -,   整理得      y=4000(1+0.5%)-.(=1,2,36)      (3)因为y=0,所以         4000(1+0.5%)-=0   即每月还款数         =(元)   所以每月的款额为121.69元.[说明] 解应用题先要认真阅读题目,一般分为粗读,细读,精读,准确理解题意,尤其是一些关键词:”等额还款”,”月利率”,”第i个月末还款后欠款表达式”等;理解题意后,引导学生将文字语言向数字语言转化,建立数学模型,再用数学知识解决问题,并使原问题得到尽可能圆满的解答.3.课堂练习  1.如果将例4的还款期限从三年改为一年,其他条件不变,那么每次付款额将是多少?  2.一套住房的建筑面积为100平方米,房价为9000元/平方米.买房者若先付房价的,其余款进行商业贷款,次月开始还贷款,按每月等额还款的方式十年还清欠款,贷款十年的月利率是0.54%.按月结息,买房者每月应还款多少元?(精确到元)数学建模的方法；关注学生解题的规范性,准确度及速度.4.课堂小结 (引导学生归纳,教师提炼)(1)主要内容:公式的灵活运用,求和公式解决应用问题;(2)数学思想方法:分类讨论、方程、转化与化归等.5.作业
 习题7.3  A组 11  12习题7.3  B组 9   10  七、教学设计思想数列求和问题中,蕴涵着许多重要数学思想方法.如方程思想,函数思想,递推,归纳,分类讨论等.数学教学既要使学生获得知识,更重要的是通过知识获得的过程来发展学生的思维能力.等比数列前n项和公式第(1)节课主要是公式的推导和基本应用，第(2)节课侧重于公式的灵活应用及应用公式解决实际问题,该节内容是发展学生应用能力、渗透数学思想方法的很好素材.公式的回顾主要再现公式推导思路,强化方法,巩固练习突出项数变化,分类讨论思想，补充的例1可以用通法先确定基本量再求和,但根据该题的结构特点,教师为学生探究学习创设平台,鼓励学生发现规律,推广结论,严格推理，使学生的思维向深层次发展；例2较抽象， 教师设计了三个设问,教学生如何理解题意，把文字语言转化为数学语言,把实际问题抽象成数学问题,把复杂问题转化成简单问题,强化学生应用的意识.