鲁教版 (五四制)九年级下册6 直线和圆的位置关系教学课件ppt

这是一份鲁教版 (五四制)九年级下册6 直线和圆的位置关系教学课件ppt，共15页。PPT课件主要包含了三角形与圆的位置关系，知识回顾，解∵∠A68°，∵点P是内心，∴∠1+∠256°，∴∠BPC124°，例题讲解，变式练习等内容，欢迎下载使用。
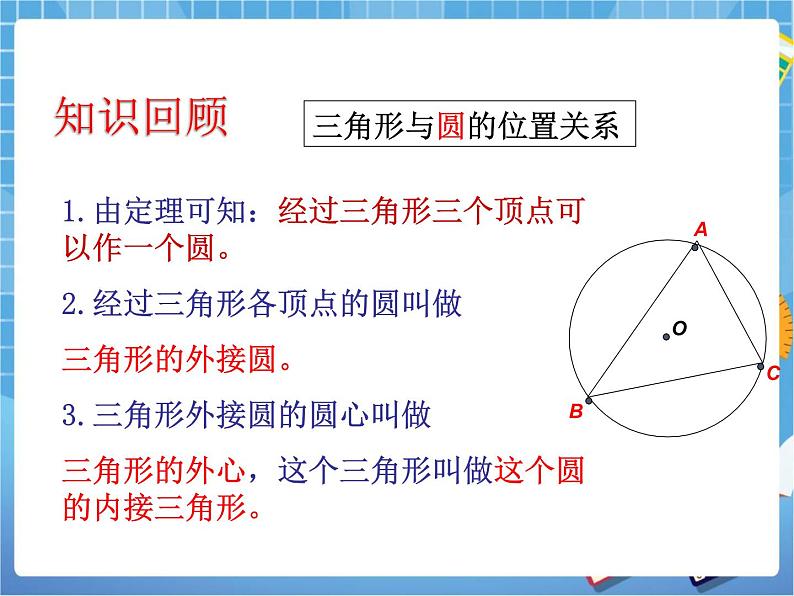
1.由定理可知：经过三角形三个顶点可以作一个圆。2.经过三角形各顶点的圆叫做三角形的外接圆。3.三角形外接圆的圆心叫做三角形的外心，这个三角形叫做这个圆的内接三角形。
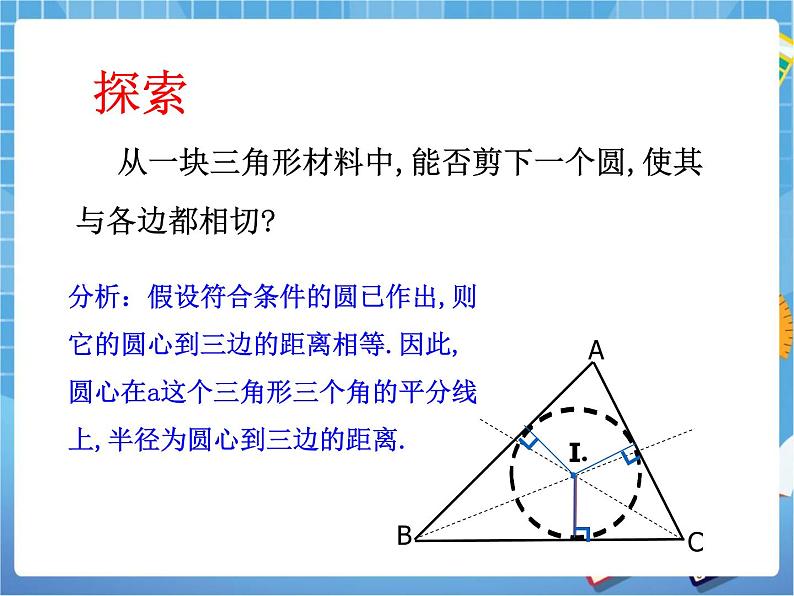
从一块三角形材料中,能否剪下一个圆,使其与各边都相切?
分析：假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在a这个三角形三个角的平分线上,半径为圆心到三边的距离.
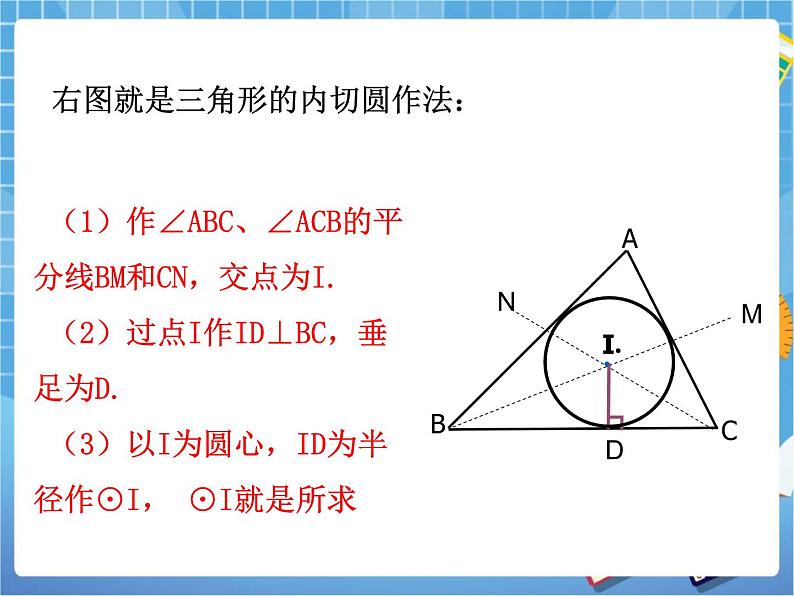
右图就是三角形的内切圆作法：
（1）作∠ABC、∠ACB的平分线BM和CN，交点为I. （2）过点I作ID⊥BC，垂足为D. （3）以I为圆心，ID为半径作⊙I， ⊙I就是所求
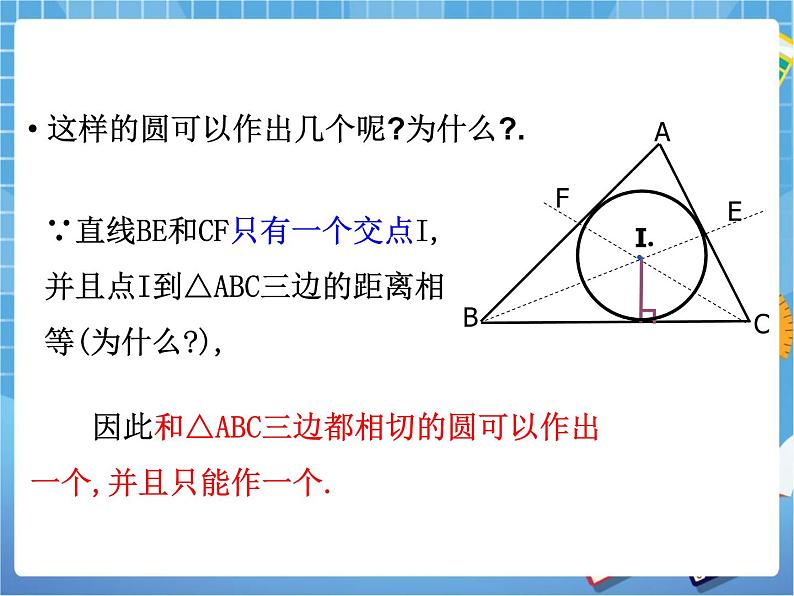
这样的圆可以作出几个呢?为什么?.
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
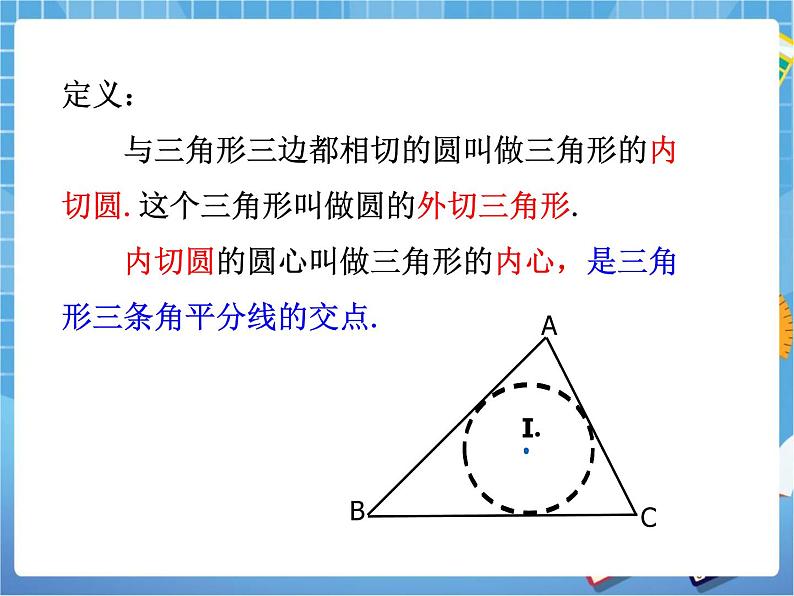
定义： 与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形. 内切圆的圆心叫做三角形的内心，是三角形三条角平分线的交点.
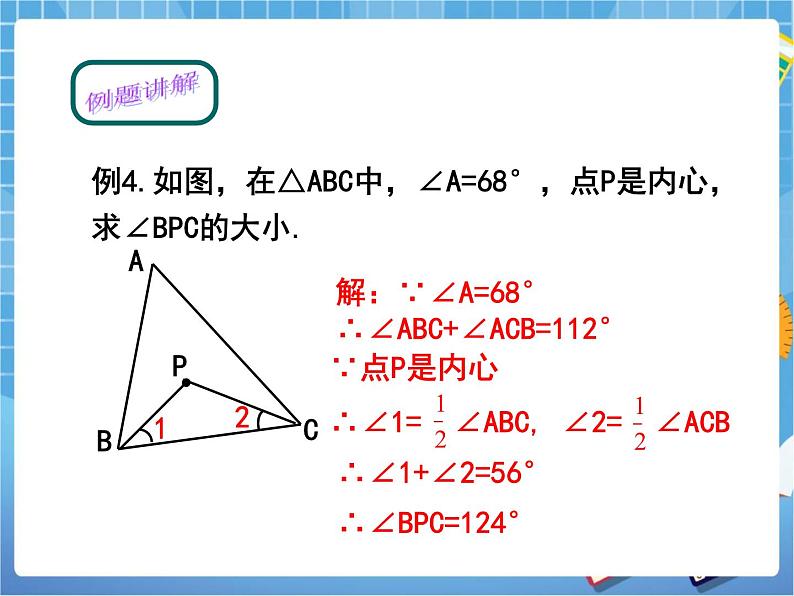
例4.如图，在△ABC中，∠A=68°，点P是内心，求∠BPC的大小.
∴∠ABC+∠ACB=112°

如图，在△ABC中，点O是内心，（1）若∠ABC=50°， ∠ACB=70°，求∠BOC的度数
（2）若∠A=80 °，则∠BOC= 度。（3）若∠BOC=110 °，则∠A= 度。
（4）试探索： ∠A与∠BOC之间存在怎样的数量关系？请说明理由。
1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?
2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?
提示:先确定圆心和半径,尺规作图要保留作图痕迹.
判断题：1、三角形的内心到三角形各个顶点的距离相等（ ）2、三角形的外心到三角形各边的距离相等 （ ）3、等边三角形的内心和外心重合； （ ）4、三角形的内心一定在三角形的内部（ ）5、菱形一定有内切圆（ ）6、矩形一定有内切圆（ ）
1.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,∠AC=3,BC=4.求⊙O的半径r.
2.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.求⊙O的半径r.
Rt△的三边长与其内切圆半径间的关系
1、已知:如图,△ABC的面积S=4cm2,周长等于10cm.求内切圆⊙O的半径r.
2、已知:如图,△ABC的面积为S,三边长分别为a,b,c.求内切圆⊙O的半径r.
斜△的三边长及面积与其内切圆半径间的关系