2012高中数学一轮复习课件《最大值、最小值》（北师大选修1-1）教案

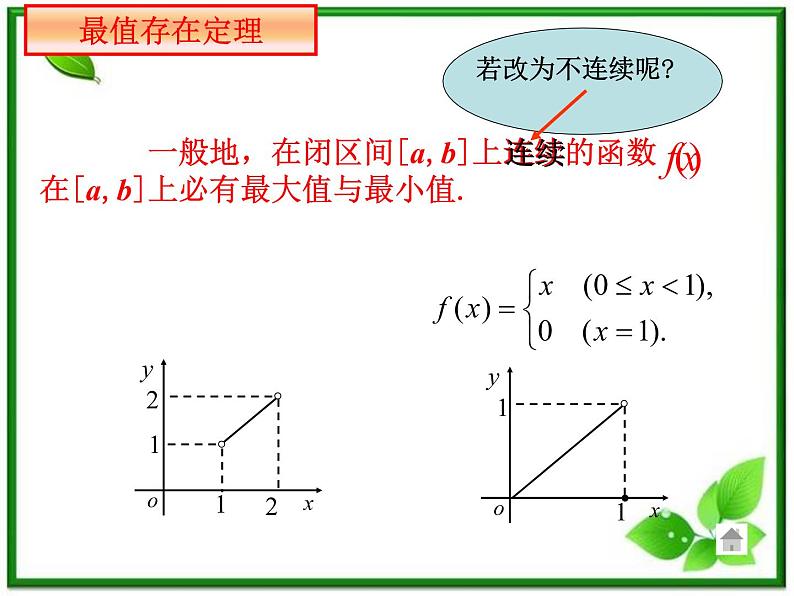
§3.8 函数的最大值与最小值高三数学选修（Ⅱ）第三章 导数与微分Maximum Value & Minimum Value of Function 实际问题 如图，有一长80cm宽60cm的矩形不锈钢薄板，用此薄板折成一个长方体无盖容器，要分别过矩形四个顶点处各挖去一个全等的小正方形，按加工要求, 长方体的高不小于10cm且不大于20cm,设长方体的高为xcm，体积为Vcm3．问x为多大时，V最大?并求这个最大值．解：由长方体的高为xcm， 可知其底面两边长分别是（80－2x） cm，（60－2x)cm, (10≤x≤20). 所以体积V与高x有以下函数关系V=（80－2x）（60－2x）x=4（40－x）（30－x）x.最值存在定理最值存在定理求 上的连续函数 的最大值与最小值的步骤:②将 f (x)的各极值与f (a)、f (b)比较，其中最大的 一个是最大值，最小的一个是最小值．求[a,b]上连续函数 最值的方法例题讲解从表上可知，最大值是13，最小值是4．13454132(1,2)1(0,1)0(-1,0)-1(-2,-1)-2+0—0+0—当x 变化时， 的变化情况如下表：单调性（2）将 的解对应的函数值f(x)与f(a)、f(b)比较，其 中最大的一个是最大值，最小的一个是最小值．例题讲解从上表可知，最大值是13，最小值是4．13454132(1,2)1(0,1)0(-1,0)-1(-2,-1)-2+0—0+0—例题讲解∴所求最大值是13，最小值是4．又（2）将 的解对应的函数值f(x)与f(a)、f(b)比较，其 中最大的一个是最大值，最小的一个是最小值．求 上的连续函数 的最大值与最小值的简化步骤:课堂练习实际问题所以体积V与高x有以下函数关系 2.求闭区间上连续函数的最值的方法与步骤; 1.在闭区间[a,b]上连续的函数在[a,b]上必有最大 值与最小值;课堂小结课外作业:教材P139 练习1、2、3. 3.利用导数求闭区间[a,b]上的连续函数最值的关键是 求得方程 (x∈ [a,b]) 的根所对应的函数值. 谢谢大家！