2020-2021学年2.1不等式的基本性质学案

知识与技能目标

1掌握与型不等式的解法，并能熟练地应用它解决问题；掌握分类讨论的方法解决含多个绝对值的不等式以及含参数的不等式；

2．理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法；掌握掌握简单的分式不等式和特殊的高次不等式的解法.

3．掌握用韦达定理解决含参二次方程的实根分布的基本方法

过程与方法目标

学生通过“回顾－反思－巩固－小结”的过程中

培养学生划归的数学思想。

情感,态度与价值观目标

数学活动充满着探索与创造，让他们在学习活动中培养独立的分析的能力。

重点

理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法

难点

理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法

活动流程图

活动内容和目的

活动1  课前热身－练习

重温概念领会新知

活动2  概念性质－反思

深刻理解定义，注意定义的内涵与外延

活动3  提高探究－实践

掌握一般方法。

活动4  归纳小结－感知

让学生在合作交流的过程总结知识和方法

活动5  巩固提高－作业

巩固教学、个体发展、全面提高

问题与情境

师生行为

设计意图

活动1课前热身（资源如下）

1、下列不等式与 同解的是（    ）

(A)    (B)   （c）(D)

2、不等式(x－2)2·(x－1)>0的解集为                .

3、不等式的整数解是_____________

4、不等式的解集为                    .

5、不等式x2+ax+b>0的解是x<－2或x>1则a=____________________,b=___________________

                .

C

1,-2

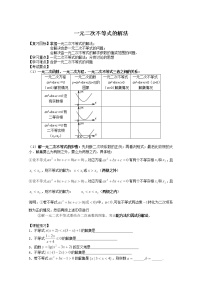
活动2知识点归纳

1解一元一次不等式

①  ②

2一元二次不等式的解法步骤

对于一元二次不等式，设相应的一元二次方程的两根为，，则不等式的解的各种情况如下表：

方程的根→函数草图→观察得解，对于的情况可以化为的情况解决

注意：含参数的不等式ax＋bx＋c>0恒成立问题含参不等式ax＋bx＋c>0的解集是R；其解答分a＝0(验证bx＋c>0是否恒成立)、a≠0（a<0且△<0）两种情况

3、分式不等式的解法：先移项通分标准化，则

4．绝对值不等式

含有绝对值的不等式性质

（1）当时，或

（2）

当且仅当时，且

当且仅当时，且

与型不等式与型不等式的解法与解集：

不等式的解集是;

不等式的解集是

不等式的解集为 ;

不等式的解集为

活动3提高探究

资源1、1、 解不等式（1）；（2）

解：（1）原不等式化为：

（2）原不等式化为： 

2、解不等式：|x-3|-|x+1|<1

分析：关键是去掉绝对值

方法1：零点分段讨论法（利用绝对值的代数定义）

∴原不等式的解集为{x|x>}

方法2：数形结合

从形的方面考虑，不等式|x-3|-|x+1|<1表示数轴上到3和-1两点的距离之差小于1的点

∴原不等式的解集为{x|x>}

资源2、解不等式变式

资源3、

1、已知不等式

解：由题意可知 且－5和1是方程的两根

故的值分别为

2、设关于x的不等式ax2+bx+c>0的解集为{x|α<x<β,α>0}用α、β表示关于x的不等式cx2－bx+a>0的解集

资源4、

1、关于x的不等式(m+1)x2－2(m－1)x+3(m－1)<0的解是一切实数，求实数m的取值范围.

2、已知，使不等式成立的x的值也满足关于x的不等式2x2－ax+a0，求a的取值范围.

3、若不等式对于x取任何实数均成立，求k的取值范围

解：∵

(∵4x2+6x+3恒正)，

∴原不等式对x取任何实数均成立，等价于不等式2x2-2(k-3)x+3-k>0对x取任何实数均成立

∴=[-2(k-3)]2-8(3-k)<0k2-4k+3<01<k<3

∴k的取值范围是（1，3）

活动4归纳小结

分式与高次不等式的解题基础是一元二次不等式的解法，常用方法是序轴标根法，但是要注意标根时的起点位置

活动5巩固提高

附作业

巩固发展提高