2020-2021学年6.4 一元一次方程的应用教案设计

这是一份2020-2021学年6.4 一元一次方程的应用教案设计，共7页。教案主要包含了列方程解应用题方法归纳，自主小结，布置作业等内容，欢迎下载使用。
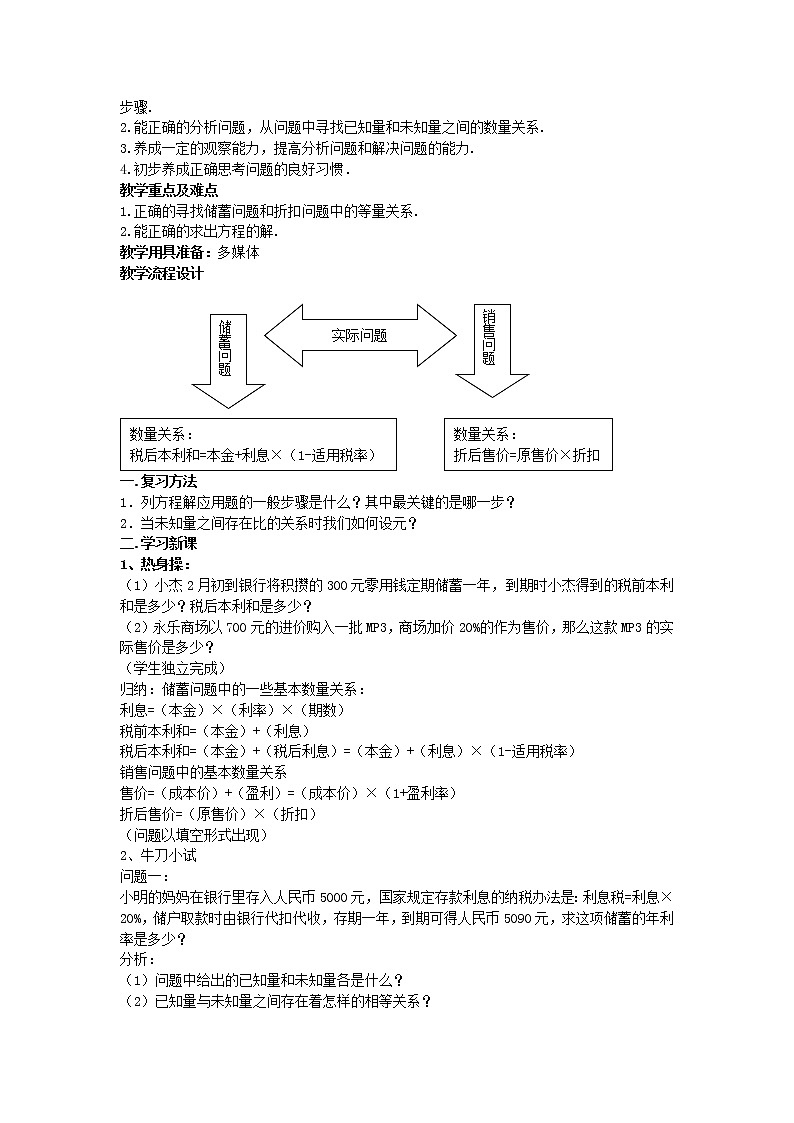
6．4（1）一元一次方程的应用教学目标1.在解决实际问题的过程中，初步掌握一元一次方程解简单应用题的方法和步骤；并会列出一元一次方程解简单的应用题.2.能正确的分析问题，从问题中找出已知量和未知量之间的数量关系.3.具有一定的观察能力，提高分析问题和解决问题的能力.4.初步养成正确思考问题的良好习惯．教学重点及难点1．元一次方程解简单的应用题的方法和步骤．2．找等量关系.3．于未知量之间存在比的关系如何设元教学用具准备：奥运图片教学流程设计   教学过程设计  一、情景引入，了解列方程解应用题优越性看一看：北京奥运的会标和吉祥物.想一想：2008年中国将举办北京奥运会.中国政府提出了“节俭办奥运”的新理念，将建造国家体育馆的预算资金调整为26亿元，比原预算节约资金35%，问原建造国家体育馆的预算资金为多少亿元？（学生独立完成，选择用算术方法解题和列方程解题的同学板演.）解法一：26÷（1-35%）=40（亿元）解法二：设原建造国家体育馆的预算资金为x亿元.x-35%x=26解方程，得x=40答：原建造国家体育馆的预算资金为40亿元.想一想：在小学算术中，我们已经学习了用算术方法解决实际问题的有关知识，而实际问题也能应用一元一次方程来解决呢.用一元一次方程解应用题与用算术方法解应用题相比较，它有什么优越性呢？ 归纳：算术方法不易思考，而应用设未知数，列出方程并通过解方程求得应用题的解的方法，有一种化难为易之感，这就是我们学习运用一元一次方程解应用题的目的之一．方程是一个含有未知数的等式，而等式表示了一个相等关系．因此对于任何一个应用题中提供的条件，应首先从中找出一个相等关系，然后再将这个相等关系表示成方程．本节课，我们就通过实例来说明怎样寻找一个相等的关系和把这个相等关系转化为方程的方法和步骤．二、研究列方程解应用题的一般步骤和方法图片引出问题：   在2004年雅典奥运会闭幕式上，中国表演队必须用8分49秒表演舞动北京、中华武术、少儿京剧等节目，其中表演的时间之比是10：8：5，那么舞动北京、中华武术、少儿京剧等节目表演的时间各是多少秒？师生共同分析：1．本题中给出的已知量和未知量各是什么？2．已知量与未知量之间存在着怎样的相等关系？舞动北京的表演时间+中华武术的表演时间+少儿京剧的表演时间=8分49秒3．若设舞动北京的表演时间为x秒，那么中华武术的表演时间和少儿京剧的表演时间如何用x表示？4．若设舞动北京的表演时间为10x秒，那么中华武术的表演时间和少儿京剧的表演时间如何用x表示？这里的x表示什么？5．在解决这个实际问题时还需要注意哪个问题？（单位问题）解：设舞动北京的表演时间为10x秒，那么中华武术的表演时间和少儿京剧的表演时间分别为8x秒和5x秒.10x+8x+5x=52923x=529x=23所以，10x=230，8x=184，5x=115.答：舞动北京的表演时间为230秒，中华武术的表演时间为184秒，少儿京剧的表演时间为115秒.练一练：书P49  1、2三、列方程解应用题方法归纳1、想一想：你能根据刚才列方程解应用题的过程说一说列方程解应用题的一般步骤吗？设未知数（元）     列方程     解方程      检验并作答许多实际问题中的已知量与未知量之间存在着等量关系，把这种等量关系式写出来，得到方程的解，通过检验获得实际问题的解，称这样的方法为方程的思想方法.2、想一想：当实际问题中未知量之间存在比的关系时，我们如何设元？四、自主小结：今天这节课你最大的收获是什么？五、布置作业：略6．4（2）一元一次方程的应用教学目标1.在解决储蓄问题和折扣问题的过程中，进一步掌握列一元一次方程解简单应用题的方法和步骤.2.能正确的分析问题，从问题中寻找已知量和未知量之间的数量关系.3.养成一定的观察能力，提高分析问题和解决问题的能力.4.初步养成正确思考问题的良好习惯．教学重点及难点1.正确的寻找储蓄问题和折扣问题中的等量关系.2.能正确的求出方程的解.教学用具准备：多媒体教学流程设计        教学过程设计一.复习方法1．列方程解应用题的一般步骤是什么？其中最关键的是哪一步？2．当未知量之间存在比的关系时我们如何设元？二.学习新课1、热身操：（1）小杰2月初到银行将积攒的300元零用钱定期储蓄一年，到期时小杰得到的税前本利和是多少？税后本利和是多少？（2）永乐商场以700元的进价购入一批MP3，商场加价20%的作为售价，那么这款MP3的实际售价是多少？（学生独立完成）归纳：储蓄问题中的一些基本数量关系：利息=（本金）×（利率）×（期数）税前本利和=（本金）+（利息）税后本利和=（本金）+（税后利息）=（本金）+（利息）×（1-适用税率）销售问题中的基本数量关系售价=（成本价）+（盈利）=（成本价）×（1+盈利率）折后售价=（原售价）×（折扣）（问题以填空形式出现）2、牛刀小试问题一：小明的妈妈在银行里存入人民币5000元，国家规定存款利息的纳税办法是：利息税=利息×20%，储户取款时由银行代扣代收，存期一年，到期可得人民币5090元，求这项储蓄的年利率是多少？分析：（1）问题中给出的已知量和未知量各是什么？（2）已知量与未知量之间存在着怎样的相等关系？本金+利息×1-适用税率=税后本利和解 设这项储蓄的年利率是x.根据题意，得  5000+5000×x×1×（1-20%）=5090                5000+4000x=50904000x=90x=0.0225所以x=2.25%答：这项储蓄的年利率是2.25%.问题二：一种节能型冰箱，商店按原售价的九折出售，降价后的新售价是每台2430元，因为商店按进价加价20%作为售价，所以降价后商店还能赚钱，请问，这种节能型冰箱的进价是多少元？按降价后的新售价出售，商店每台还可赚多少元？分析：（1）问题中给出的已知量和未知量各是什么？（2）已知量与未知量之间存在着怎样的相等关系？原售价×折扣=折后售价（3）如果设这种节能型冰箱的进价是x元，那么这台节能型冰箱的原售价如何用x表示呢？解 设这种节能型冰箱的进价是x元，那么每台冰箱原售价是（1+20%）x.根据题意，得    （1+20%）x·90%=2430                        1．08x=2430x=22502430-2250=180（元）答：这种节能型冰箱的进价是2250元.按降价后的新售价出售，商店每台还可赚180元.1、              练一练：P51  1、2三.学习心得交流1、今天我学会了解决哪些实际问题？2、这些实际问题中存在哪些基本数量关系？四.布置作业：1、基本作业：略 2、拓展作业：请自编一道有关储蓄问题和销售问题的应用题.6．4（3）一元一次方程的应用教学目标1.在解决行程问题的过程中，进一步掌握列一元一次方程解简单应用题的方法和步骤.2.在不同类型的行程问题中能正确的分析问题，从问题中寻找已知量和未知量之间的数量关系.3.提高分析问题和解决问题的能力，初步体会分类讨论的数学思想.4.初步养成正确思考问题的良好习惯．教学重点及难点：在不同类型的行程问题中能正确的分析问题，从问题中寻找已知量和未知量之间的数量关系.教学用具准备：多媒体设备、课前体育课中的跑步竞赛教学过程设计一.复习旧知识1、在小学你会解决哪些实际问题？在行程问题中的基本数量关系是什么？路程=速度×时间速度=路程÷时间=时间=路程÷速度=（S=vt、、其中，S：路程，v：速度，t：时间）2、看你行不行（学生独立完成）甲，乙两地相距162千米，甲地有一辆货车，速度为每小时48千米，乙地有一辆客车，速度为每小时60千米，求：（1）若两车同时相向而行，多长时间可以相遇？（2）若两车同时背向而行，多长时间两车相距270千米？（3）若两车相向而行，货车先开1小时，再过多长时间可以相遇？分析：在行程问题，我们可以先画示意图，从图中就可以得到等量关系解（1）设x小时可以相遇则由题意可列：48x+60x=162解得x=1.5答：1.5小时后可以相遇.（2）设x小时两车相距270千米则由题意可列：48x+162+60x=270解得x=1答：1小时后两车相距270千米.（3）设再过x小时两车可以相遇则由题意可列：48(x+1)+60x=162解得答：小时两车可以相遇.二.学习新课1、回顾跑步比赛：在环行跑道上游戏，老师安排了几种比赛形式？这两种不同的的形式有什么区别？2、解决新问题：问题一：如右图：小杰、小丽分别在400米环形跑道上练习跑步与竞走，小杰每分钟跑320米，小丽每分钟跑120米，两人同时由同一点出发，问几分钟后，小丽与小杰第一次相遇？分析：（1）       问题中给出的已知量和未知量各是什么？（2）       图中给出了什么信息？（3）如果设x分钟后，小丽与小杰第一次相遇，请试着完成下表：  路程速度时间小丽   小杰   （4）已知量与未知量之间存在着怎样的相等关系？小杰跑的路程-小丽走的路程=环形跑道一周的长解：设x分钟后，小丽与小杰第一次相遇.320x-120x=400解方程得          x=2答：2分钟后，小丽与小杰第一次相遇.问题二：小杰、小丽分别在400米环形跑道上练习跑步与竞走，小杰每分钟跑320米，小丽每分钟跑120米，两人同时由同一点反向而跑，问几分钟后，小丽与小杰第一次相遇？分析：已知量与未知量之间存在着怎样的相等关系？小杰跑的路程+小丽走的路程=环形跑道一周的长解：设x分钟后，小丽与小杰第一次相遇.320x+120x=400解方程得           x=答：分钟后，小丽与小杰第一次相遇.问题三：小杰、小丽分别在400米环形跑道上练习跑步与竞走，小杰每分钟跑320米，小丽每分钟跑120米，两人同时由同一点出发，问几分钟后，小丽与小杰第一次相遇？分析：此问题会有几种情况出现？已知量与未知量之间存在着怎样的相等关系？情况一：小杰跑的路程-小丽走的路程=环形跑道一周的长情况二：小杰跑的路程+小丽走的路程=环形跑道一周的长3、练一练：P 51  3、4三.自主小结1.今天我学会解决了哪一类的行程问题？2.在分析行程问题中的等量关系时我们有哪几种方法？3.在解决行程问题中我们要注意什么？（单位换算问题）四、布置作业1.基本练习：略2.拓展练习：甲，乙两地相距162千米，甲地有一辆货车，速度为每小时48千米，乙地有一辆客车，速度为每小时60千米，求：（1）若两车同时相向而行，货车在路上耽误了半小时，多长时间可以相遇？（3）       若两车相向而行，同时出发，多长时间两车相距54千米？