2021学年7.6 余角、补角教案

这是一份2021学年7.6 余角、补角教案，共4页。教案主要包含了教学目标，教学重点，教学难点，教学过程等内容，欢迎下载使用。
【教学重点】1. 理解余角、补角的概念，会求已知角的余角或补角.2. 理解余角（补角）的性质，会用性质及建立方程的思想方法求有关角的度数.
【教学难点】1.理解余角（补角）的性质，会用性质及建立方程的思想方法求有关角的度数.2. 理解互余（及互补）两角的等式表示方法.
【教学过程】
一．情景引入
1.观察与思考：出示图1、图2，当∠ABC=90°，∠DEF=180°时，图中∠1与∠2、∠3与∠4之间有什么特殊关系？

图1 图2
说明：让每位学生通过观察得出∠1+∠2=90°，∠3+∠4=180°。即两个角之和正好成一直角，或两个角之和正好成一平角，在这种情况下，我们给出两个新的概念。
二．学习新课
（一）阅读课本P103页的第二段后，找出概念中的关键词并交流。
1．互为余角定义：如果两个角的度数的和是90度，那么这两个角叫做互为余角，简称互余。其中一个角称为另一个角的余角。
2．互为补角定义：如果两个角的度数的和是180度，那么这两个角叫做互为补角．简称互补。其中一个角称为另一个角的补角。
3.那么图中互余两角的数学式子表示：
若∠1+∠2=90°，那么∠1与∠2互余，∠1是∠2的余角，同样∠2也是∠1的余角；用等式表示是∠2=90⁰-∠1，∠1=90⁰-∠2
反之若∠1与∠2互余，那么∠1+∠2=90°
4．互补两角的数学式子表示：
若∠1+∠2=180°，那么∠1与∠2互补，即∠1是∠2的补角，同样∠2也是∠1的补角；
用等式表示是∠2=180⁰-∠1，∠1=180⁰-∠2
反之若∠1与∠2互补，那么∠1+∠2=180°。
说明：要让学生理解余角（补角）是对另一个角而言，而互余（互补）是表示两个角之间的关系.这里要让学生体验几何语言的表述的简洁性；互余两角的数学式子表示可以在教师的启发下，由学生归纳出，而互补两个角的数学式子由学生模仿独立说出、写出，培养学生对知识的迁移能力和概括归纳能力.
5.练习：
（1）在一副三角尺中，有没有互余的两个角？
（2）图中给出的各角中,哪些互为余角?哪些互为补角?

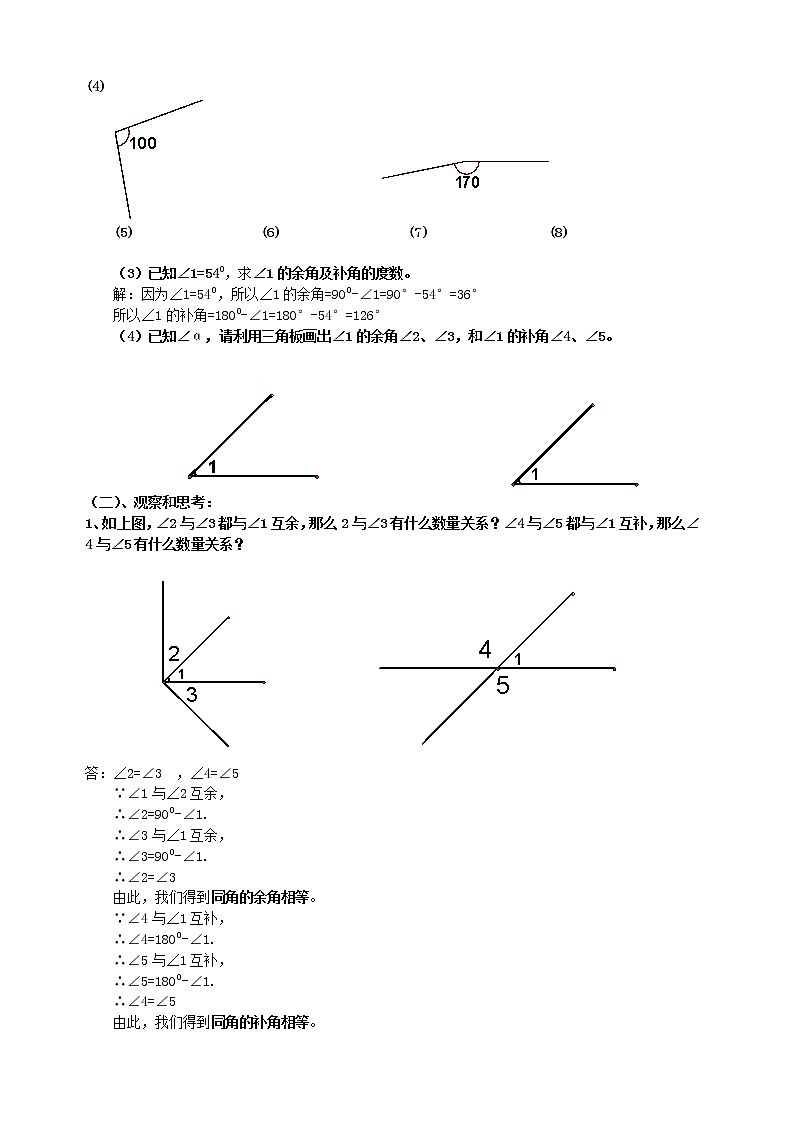
（1） (2) (3) (4)


(5) (6) (7) (8)
（3）已知∠1=54⁰，求∠1的余角及补角的度数。
解：因为∠1=54⁰，所以∠1的余角=90⁰-∠1=90°-54°=36°
所以∠1的补角=180⁰-∠1=180°-54°=126°
（4）已知∠α，请利用三角板画出∠1的余角∠2、∠3，和∠1的补角∠4、∠5。
（二）、观察和思考：
1、如上图，∠2与∠3都与∠1互余，那么2与∠3有什么数量关系？∠4与∠5都与∠1互补，那么∠4与∠5有什么数量关系？
答：∠2=∠3 ，∠4=∠5
∵∠1与∠2互余，
∴∠2=90⁰-∠1.
∴∠3与∠1互余，
∴∠3=90⁰-∠1.
∴∠2=∠3
由此，我们得到同角的余角相等。
∵∠4与∠1互补，
∴∠4=180⁰-∠1.
∴∠5与∠1互补，
∴∠5=180⁰-∠1.
∴∠4=∠5
由此，我们得到同角的补角相等。同样可得：等角的余角相等。等角的补角相等。
2.练习：如图所示，已知∠AOC=∠BOD=90⁰，
（1）∠AOD与∠BOC有什么关系？为什么？
（2）若∠DOC=35⁰，则∠AOD、∠AOB等于多少度？
（3）若∠AOB=150⁰，则∠DOC等于多少度？
解：（1）∠AOD=∠BOC.理由如下：由已知∠AOC=∠BOD=90⁰,
∠AOD+∠DOC=90⁰,∠BOC+∠DOC=90⁰,
所以∠AOD=∠BOC(同角的余角相等)。
（2）由已知∠DOC=35⁰,
所以∠AOD=∠BOC=90⁰-35⁰=55⁰，
所以∠AOB=∠AOD+∠DOC+∠BOC=55⁰+35⁰+55⁰=145⁰.
(3)由已知∠AOC=∠BOD=90⁰，∠AOB=150⁰，
所以∠AOD=∠AOB-∠BOD=150⁰-90⁰=60⁰，
所以∠DOC=∠AOC-∠AOD=90⁰-60⁰=30⁰.
（三）、角的度量单位
1、思考：角是有大小的，它的度量单位有那些？
角的度量单位有度、分、秒，它们的关系是：
1⁰=60’，1’=60”.这是60进位制。
说明：重点让学生掌握60进位制.
2.练习：
（1）90°=89° ′；180°=179° ′
（2）32°27′=31° ′；125°66′= °6′
3.例题分析
（1）例题1：计算下列各式：
（1）77°54′36″+34°27′44″；
（2）89°6′4″-24°27′35″；
（3）90°-35°24′15″
（4）180°-125°36′48″
（2）例题2：已知∠1=53°38′，求∠1的余角及补角的度数.
（3）例题3：已知一个角的补角是这个角的余角的3倍，求这个角的度数.
分析：要求这个角怎样用含未知数的代数式表示这个角的补角和这个角的余角？
说明：例题1的四个小题，主要让学生能够熟练进行角的和差的计算以及度、分、秒三种单位之间的换算，强调两点，一是同级单位进行加减，二是如果计算结果中出现超过60分或60秒，必须分别向上一级单位进位，三是在减法中，遇到被减数中的分、秒数小于减数的分、秒数，那么要向上一级单位借.在学生笔算的基础上，再让学生分别用计算器进行验算检查刚才计算是否正确.在例题1的基础上，容易求出例题2的结果.例题3重点让学生掌握方程是解决实际问题常用的数学方法.
三.课堂小结：
今天我们学习到了什么？你感兴趣的是什么？
四．课堂检测：
1、填空题：
（1）、已知：∠1=20°，∠2=30°，∠3=60°，∠4=150°，则∠2是 的余角，
是∠4的补角。
（2）、若∠1+∠2=90°，∠3+∠2=90°，∠1=40°，则∠3= 。
（3）、∠1和∠3互余，∠2和∠3互补
①若∠3=15°，则∠1= ，∠2= ；
②若∠3=36°，则∠1= ，∠2= ；
③若∠3=70°，则∠1= ，∠2= ；
④若∠3=x°，则∠1= ，∠2= ；
二、计算下列各式：
4、72°51′3″+34°7′24″ 5、82°6′43″-24°27′35″
6、90°-35°23′15″ 7、180°-113°34′44″
三、如图：已知∠AOB=72°，射线OC平分∠AOB，OD⊥OC，求∠AOD的度数
四、已知一个角的补角是这个角的余角的4倍，求这个角的度数。
五．布置作业：习题7.6