初中数学苏科版七年级上册6.5 垂直随堂练习题

这是一份初中数学苏科版七年级上册6.5 垂直随堂练习题，共14页。试卷主要包含了5垂直练习，下列说法错误的是等内容，欢迎下载使用。

一、单选题
1.点P为直线外一点，点A、B在直线l上，若PA=4cm，PB=5cm，则点P到直线l的距离是( )
A. 4cm B. 小于4cm C. 不大于4cm D. 5cm
2.如图， P 是直线 l 外一点，从点 P 向直线 l 引 PA ， PB ， PC ， PD 几条线段，其中只有 PB 与 l 垂直，这几条线段中长度最短的是（ ）
A. PA B. PB C. PC D. PD
3.点P为直线l外一点，点A、B、C为直线l上三点，PA=4cm、PB=5cm、PC=2cm，则点P到直线l的距离（ ）
A. 等于4cm B. 等于2cm C. 小于2cm D. 不大于2cm
4.下列说法错误的是（ ）
A. 平面内过一点有且只有一条直线与已知直线平行
B. 平面内过一点有且只有一条直线与已知直线垂直
C. 两点之间的所有连线中，线段最短
D. 对顶角相等
5.如图, P 为直线 l 外一点,点 A 、 B 、 C 在直线 l 上,且 PB⊥l ,垂足为 B , ∠APC=90° ,则下列说法错误的是（ ）
A. 线段 PB 的长叫做点 P 到直线 l 的距离 B. PA 、 PB 、 PC 三条线段中, PB 最短
C. 线段 AC 的长等于点 P 到直线 l 的距离 D. 线段 PA 的长叫做点 A 到直线 PC 的距离
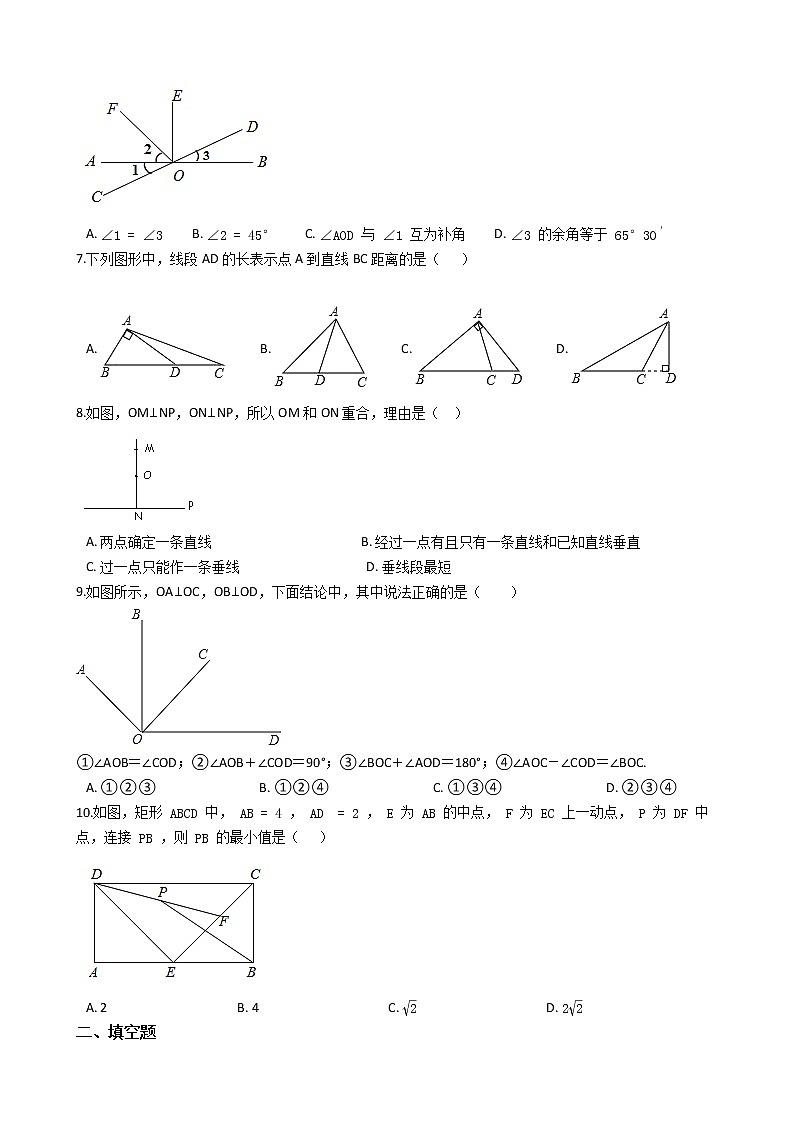
6.如图，直线 AB,CD 相交于点 O,OE⊥AB 于点 O,OF 平分 ∠AOE,∠1=25°30' ，则下列结论中不正确的是（ ）
A. ∠1=∠3 B. ∠2=45° C. ∠AOD 与 ∠1 互为补角 D. ∠3 的余角等于 65°30′
7.下列图形中，线段AD的长表示点A到直线BC距离的是（ ）

A. B. C. D.
8.如图，OM⊥NP，ON⊥NP，所以OM和ON重合，理由是（ ）
A. 两点确定一条直线 B. 经过一点有且只有一条直线和已知直线垂直
C. 过一点只能作一条垂线 D. 垂线段最短
9.如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（ ）
①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.
A. ①②③ B. ①②④ C. ①③④ D. ②③④
10.如图，矩形 ABCD 中， AB=4 ， AD=2 ， E 为 AB 的中点， F 为 EC 上一动点， P 为 DF 中点，连接 PB ，则 PB 的最小值是（ ）
A. 2 B. 4 C. 2 D. 22
二、填空题
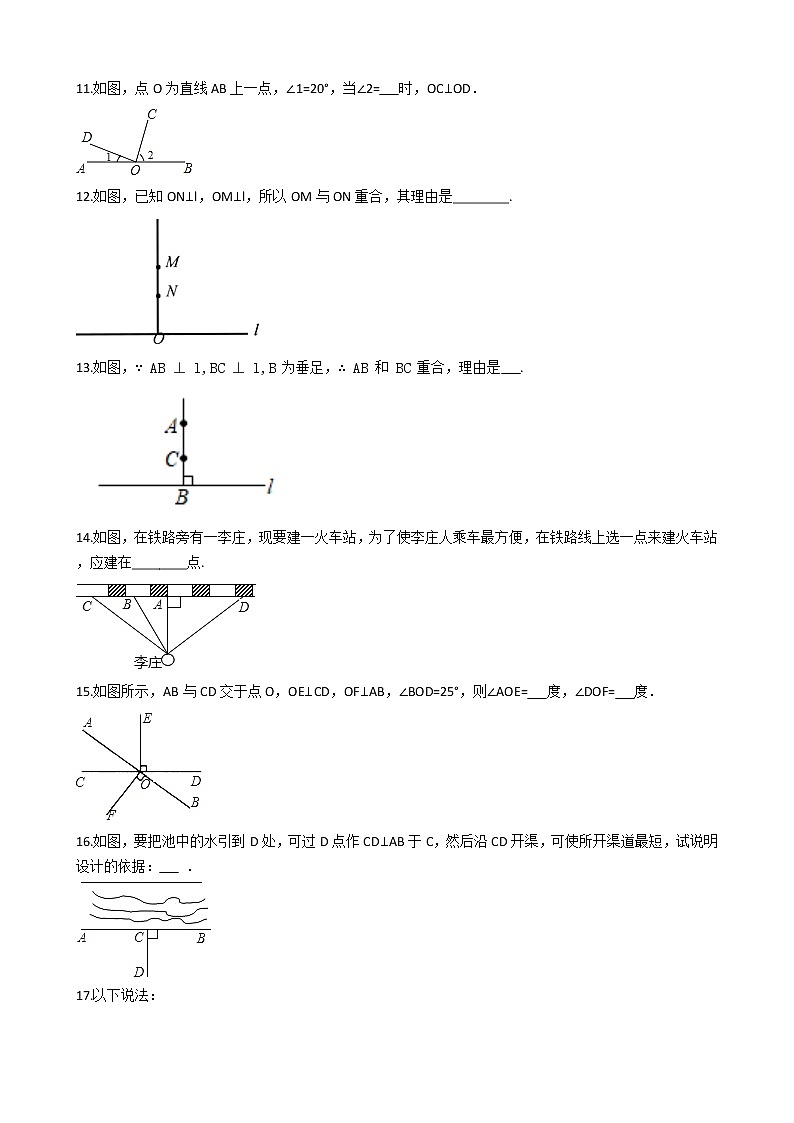
11.如图，点O为直线AB上一点，∠1=20°，当∠2= 时，OC⊥OD．
12.如图，已知ON⊥l，OM⊥l，所以OM与ON重合，其理由是________.
13.如图，∵ AB⊥l,BC⊥l,B 为垂足，∴ AB 和 BC 重合，理由是 .
14.如图，在铁路旁有一李庄，现要建一火车站，为了使李庄人乘车最方便，在铁路线上选一点来建火车站，应建在________点.
15.如图所示，AB与CD交于点O，OE⊥CD，OF⊥AB，∠BOD=25°，则∠AOE= 度，∠DOF= 度．
16.如图，要把池中的水引到D处，可过D点作CD⊥AB于C，然后沿CD开渠，可使所开渠道最短，试说明设计的依据： ．
17.以下说法：
①两点确定一条直线；
②一条直线有且只有一条垂线；
③不相等的两个角一定不是对顶角；
④若|a|=﹣a，则a＜0；
⑤若a，b互为相反数，则a，b的商必定等于﹣1．
其中正确的是 ． （请填序号）
18.如图，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周，在旋转的过程中，当第 秒时，直线CD恰好与直线MN垂直．
三、解答题
19.如图所示，射线OM与直线交于点O，OM平分∠AOB，求∠AOM度数，并用符号表示OM与AB的位置关系．
20.如图所示，已知AO⊥BC于O，DO⊥OE，∠1=65°，求∠2的度数．
21.如图，直线AB与直线CD相交于点O，OE⊥AB，已知∠BOD＝45°，求∠COE的度数．
22.如图，直线AB与直线CD相交于点O，OE⊥AB，已知∠BOD=45°，求∠COE的度数．
23.如图，OA⊥OB，OC⊥OD，∠BOC﹣∠AOD=40°，求∠BOC与∠AOD的大小．
24.如图，直线AB、CD、EF都经过点O，且AB⊥CD，∠COE=35°，求∠DOF、∠BOF的度数．
25.已知：OA⊥OC，∠AOB：∠AOC=2：3，画出图形，并求∠BOC的度数．
26.如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？
27.如图，已知A，O，E三点在一条直线上，OB平分∠AOC，∠AOB＋∠DOE＝90°，试问：∠COD与∠DOE之间有怎样的关系?说明理由.－cm
28.如图，已知直线AB与CD相交于点O ， OE平分∠AOC ， 射线OF⊥CD于点O ， 且∠BOF=32°，求∠COE的度数．
答案解析部分
一、单选题
1.【答案】 C
【考点】垂线段最短
【解析】【解答】依据垂线段最短，∵P为直线外一点，点A、B在直线l上，若PA=4cm，PB=5cm，∴点P到直线l的距离不大于4cm，故答案为C.
【分析】依据点到直线的距离垂线段最短，即可求解..
2.【答案】 B
【考点】垂线段最短
【解析】【解答】解：直线外一点 P 与直线上各点连接的所有线段中，最短的是 PB ，依据是垂线段最短．
故答案为：B．

【分析】根据垂线段最短的性质可得答案。
3.【答案】 D
【考点】点到直线的距离
【解析】【解答】解：当PC⊥l时，PC是点P到直线l的距离，即点P到直线l的距离2cm，
当PC不垂直直线l时，点P到直线l的距离小于PC的长，即点P到直线l的距离小于2cm，
综上所述：点P到直线l的距离不大于2cm，
故选：D．
【分析】根据点到直线的距离是直线外的点与直线上垂足间的线段的长，再根据垂线段最短，可得答案．
4.【答案】 A
【考点】垂线段最短，对顶角及其性质
【解析】【解答】解：A、在同一平面内，过直线外一点有且只有一条直线与已知直线平行，故本选项说法错误.
B、在同一平面内，过一点有且只有一条直线与已知直线垂直，故本选项说法正确.
C、两点之间的所有连线中，线段最短，故本选项说法正确.
D、对顶角相等故本选项说法正确.
故答案为：A.
【分析】根据平行公理可判断A的正误；根据垂直公理可判断B的正误；根据线段的性质可判断C的正误；根据对顶角的性质可判断D的正误.
5.【答案】 C
【考点】垂线段最短，点到直线的距离
【解析】【解答】A. 线段 PB 的长叫做点 P 到直线 l 的距离，不符合题意；
B. PA 、 PB 、 PC 三条线段中, PB 为垂线段，故最短，不符合题意；
C. 线段 AC 的长为A与C的线段长度，故符合题意；
D. 线段 PA 的长叫做点 A 到直线 PC 的距离，不符合题意
故答案为：C.
【分析】根据垂线的定义即可求解.
6.【答案】 D
【考点】角的运算，余角、补角及其性质，垂线
【解析】【解答】A、∵AB、CD相交于O点，∴ ∠1=∠3 正确，符合题意；
B、∵OE⊥AB于点O，OF平分∠AOE，∴ ∠2=45° 正确，符合题意；
C、∵OD过直线AB上一点O，∴ ∠AOD 与 ∠1 互为补角，正确，符合题意；
D、 ∠3 的余角等于 90°−25°30′=64°30′ ，原说法错误，不合题意，
故答案为：D.
【分析】A、根据对顶角的性质判断即可；
B、根据垂直的概念以及角平分线的概念判断即可；
C、根据补角的概念判断即可；
D、根据余角的概念可得∠3的余角=90°-∠3=90°-∠1，据此判断即可.
7.【答案】 D
【考点】点到直线的距离
【解析】【解答】解：点A到直线BC的距离，为三角形ABC，边BC上的高
故答案为：D.

【分析】根据题意可知，点A到直线BC的距离，为三角形ABC，边BC上的高，进行判断得到答案即可。
8.【答案】 B
【考点】垂线
【解析】【解答】概念理解型题．经过一点有且只有一条直线与已知直线垂直．因为OM⊥NP，ON⊥NP，两条经过O点的直线都垂直于NP，所以选B．
【分析】概念理解型题，掌握经过一点有且只有一条直线与已知直线垂直，是解答本题的关键．本题考查垂线．
9.【答案】 C
【考点】垂线
【解析】【解答】由题意可知，OA⊥OC，所以∠AOC＝90°，即∠AOB＋∠BOC＝90°．同时，OB⊥OD，所以∠BOD＝90°，即∠COD＋∠BOC＝90°．依次，可以判定∠AOB＝∠COD，所以①正确．又因为不能推断出∠AOB与∠COD的具体角度，所以②不正确．∠AOD＝∠AOB＋∠BOC＋∠COD，所以∠BOC＋∠AOD＝∠BOC＋∠AOB＋∠BOC＋∠COD＝90°＋90°＝180°．因为∠AOB＝∠COD，所以∠AOC－∠COD＝∠AOC－∠AOB＝∠BOC，所以④正确．为此，选C．
【分析】在掌握两直线相互垂直，夹角为直角的基础上，学会角度转换，就能轻松找到正确答案．本题考查垂线．
10.【答案】 D
【考点】垂线段最短
【解析】【解答】解：如图

当点F与点C重合时，点P在P1处，CP1=DP1 ,
当点F与点E重合时，点P在P2处，EP2=DP2,
.".P1P2//CE且PiP2=2CE.
当点F在EC上除点C、E的位置处时，有DP=FP .
中位线定理可知∶P1P//CE且P1P=12CF .
∴点P的运动轨迹是线段P1P2 ，
∴当BP⊥P1P2时，PB取得最小值﹒

当C和F重合时，P点是CD的中点，此时∠BP1P2=90°
CP=2
∴BP=BC2+CP2=22+22=22
故答案为：D.

【分析】由P点的运动轨迹可知，P点始终在DE和CD中点的连线上，则PB最小值是点P到连线的距离，即以CD中点和点B为端点的线段长，在直角三角形中利用勾股定理求解即可。
二、填空题
11.【答案】 70°
【考点】垂线
【解析】【解答】解：当∠2=70°时，OC⊥OD，
理由：∵∠1+∠2+∠DOC=180°，
∴∠DOC=180°﹣∠1﹣∠2，
∵∠1=20°，∠2=70°，
∴∠DOC=90°，
∴OC⊥OD．
故答案为：70°．
【分析】当∠2=70°时，OC⊥OD，根据平角定义可得∠1+∠2+∠DOC=180°，进而得到∠DOC=180°﹣∠1﹣∠2，再把∠1，∠2的度数代入即可算出∠DOC=90°，根据垂直定义可得OC⊥OD．
12.【答案】 过一点有且只有一条直线与已知直线垂直
【考点】垂线
【解析】【解答】∵OM⊥l，ON⊥l，
∴OM与ON重合（平面内，经过一点有且只有一条直线与已知直线垂直），
故答案为：平面内，经过一点有且只有一条直线与已知直线垂直．
【分析】平面内，经过一点有且只有一条直线与已知直线垂直，据此可得结论．
13.【答案】 在同一平面内，过一点有且只有一条直线与已知直线垂直
【考点】垂线
【解析】【解答】解：如图，∵ AB⊥l,BC⊥l,B 为垂足，∴ AB 和 BC 重合，理由是：在同一平面内，过一点有且只有一条直线与已知直线垂直.
故答案为：在同一平面内，过一点有且只有一条直线与已知直线垂直.
【分析】在同一平面内，过一点有且只有一条直线与已知直线垂直，据此解答即可.
14.【答案】 A
【考点】垂线段最短
【解析】【解答】解：根据垂线段最短可得：应建在A点，
故答案为：A.
【分析】根据垂线段最短即可求出答案.
15.【答案】 65；115
【考点】垂线
【解析】【解答】解：∵OE⊥CD，OF⊥AB，
∴∠DOE=∠BOF=90°，
∵∠AOE+∠DOE+∠BOD=∠AOB，∠BOD=25°，
∴∠AOE+90°+25°=180°，
解得∠AOE=65°，
∴∠DOF=∠BOF+∠BOD
=90°+25°=115°．
故填65，115．
【分析】利用平角关系∠AOE+∠DOE+∠BOD=∠AOB，可求∠AOE，再利用角的和差关系求∠DOF．
16.【答案】 垂线段最短
【考点】垂线段最短
【解析】【解答】解：过D点引CD⊥AB于C，然后沿CD开渠，可使所开渠道最短，根据垂线段最短．
【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．
17.【答案】 ①③
【考点】相反数及有理数的相反数，绝对值及有理数的绝对值，直线的性质：两点确定一条直线，垂线，对顶角及其性质
【解析】【解答】解：①两点确定一条直线；正确；
②一条直线有且只有一条垂线；错误；
③不相等的两个角一定不是对顶角；正确；
④若|a|=﹣a，则a＜0；错误，a=0也存立；
⑤⑤若a，b互为相反数，那么a，b的商必定等于﹣1，其中a，b不为0，故错误．
正确的有①③，
故答案为①③．
【分析】利用直线的性质以及相反数和绝对值以及等式的性质、垂线的知识分别判断得出答案即可．
18.【答案】 5.5或11.5
【考点】垂线
【解析】【解答】解：如图，CD在OM的右边时，设CD与AB相交于G，
∵CD⊥MN，
∴∠NGC=90°﹣∠MNO=90°﹣30°=60°，
∴∠CON=∠NGC﹣∠OCD=60°﹣45°=15°，
∴旋转角为180°﹣∠CON=180°﹣15°=165°，
t=165°÷30°=5.5秒，
CD在OM的左边时，设CD与AB相交于G，
∵CD⊥MN，
∴∠NGD=90°﹣∠MNO=90°﹣30°=60°，
∴∠AOC=∠NGD﹣∠C=60°﹣45°=15°，
∴旋转角为360°﹣∠AOC=360°﹣15°=345°，
t=345°÷30°=11.5秒，
综上所述，第5.5或11.5秒时，直线CD恰好与直线MN垂直．
故答案为：5.5或11.5．
【分析】分CD在OM的右边时，设CD与AB相交于G，根据直角三角形两锐角互余求出∠CGN，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CON，再求出旋转角即可，CD在OM的左边时，设CD与AB相交于G，根据直角三角形两锐角互余求出∠NGD，再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AOC，然后求出旋转角，计算即可得解．
三、解答题
19.【答案】 解：∵∠AOB=180°，OM平分∠AOB，
∴∠AOM= 12 ∠AOB= 12 ×180°=90°，
∴OM⊥AB．
【考点】垂线
【解析】【分析】根据角平分线定义得出∠AOM= 12 ∠AOB，代入求出∠AOM=90°，根据垂直定义得出即可．
20.【答案】 解：∵AO⊥BC于O，
∴∠AOC=90°，
又∠1=65°，
∴∠AOE=90°﹣65°=25°．
∵DO⊥OE，
∴∠DOE=90°，
∴∠2=∠DOE﹣∠AOE=90°﹣25°=65°
【考点】垂线
【解析】【分析】由已知条件和观察图形可知∠1与∠AOE互余，∠AOE与∠2互余，利用这些关系可解此题．
21.【答案】 解：∵OE⊥AB,
∴∠AOE= 90° .
∵ ∠AOC=∠BOD=45° ,
∴ ∠COE=∠AOC+∠AOE=45°+90°=135°
【考点】垂线，对顶角及其性质
【解析】【分析】根据垂直定义求出∠AOE，根据对顶角求出∠AOC，相加即可．
22.【答案】 解：∵OE⊥AB，
∴∠AOE=90°，
∵∠AOC=∠BOD=45°，
∴∠COE=∠AOE+∠AOC=90°+45°=135°
【考点】垂线，对顶角及其性质
【解析】【分析】根据垂直定义求出∠AOE，根据对顶角求出∠AOC，相加即可．
23.【答案】 解：∠AOD+∠BOC=360°﹣（∠BOC﹣∠AOD）=360°﹣90°﹣90°=180°，
又∵∠BOC﹣∠AOD=40°，
∴∠BOC=110°，∠AOD=70°
【考点】垂线
【解析】【分析】根据∠AOD，∠BOC，∠AOB和∠COD的度数的和是360度，即可求得∠AOD+∠BOC的和，然后根据∠BOC﹣∠AOD=40°即可求解．
24.【答案】 解：如图，∵∠COE=35°，
∴∠DOF=∠COE=35°，
∵AB⊥CD，
∴∠BOD=90°，
∴∠BOF=∠BOD+∠DOF，
=90°+35°
=125°．
【考点】垂线，对顶角及其性质
【解析】【分析】根据对顶角相等得到∠DOF=∠COE，又∠BOF=∠BOD+∠DOF，代入数据计算即可．
25.【答案】 解：∵OA⊥OC，
∴∠AOC=90°，
∵∠AOB：∠AOC=2：3，
∴∠AOB=60°．
因为∠AOB的位置有两种：一种是在∠AOC内，一种是在∠AOC外．
①当在∠AOC内时，∠BOC=90°﹣60°=30°；
②当在∠AOC外时，∠BOC=90°+60°=150°．
综上所述，∠BOC的度数为30°或150°．
【考点】角的运算，垂线
【解析】【分析】根据垂直关系知∠AOC=90°，由∠AOB：∠AOC=2：3，可求∠AOB，根据∠AOB与∠AOC的位置关系，分类求解．
26.【答案】 解：如图，延长AO，先测量出∠BOC的度数， 然后根据∠AOB与∠BOC是邻补角即可求解，
∠AOB=180°﹣∠BOC．
【考点】点到直线的距离
【解析】【分析】延长∠AOB的一边，然后根据邻补角的和等于180°即可求解．
27.【答案】 相等，理由：∠AOB＋∠DOE＝90°，且A、O、E三点共线，所以∠BOC＋∠COD＝90°．因为OB平分∠AOC，所以∠AOB＝∠BOC，通过等量代换，可以得知∠COD与∠DOE相等．
【考点】垂线
【解析】【解答】由题意可知，∠AOB＋∠DOE＝90°，且A、O、E三点共线，所以∠BOC＋∠COD＝90°．因为OB平分∠AOC，所以∠AOB＝∠BOC，通过等量代换，可以得知∠COD与∠DOE相等．
【分析】掌握相交线相关知识，是解答本题的关键．本题考查垂线．
28.【答案】 解：∵∠COF是直角，∠BOF=32°， ∴∠COB=90°﹣32°=58°， ∴∠AOC=180°﹣58°=122° 又∵OE平分∠AOC， ∴∠AOE=∠COE=61°
【考点】垂线
【解析】【解答】利用图中角与角的关系即可求得．
【分析】此题主要考查了角平分线的定义，根据角平分线定义得出所求角与已知角的关系转化求解．