初中数学苏科版八年级上册6.4 用一次函数解决问题习题

这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题习题，共16页。试卷主要包含了4用一次函数解决问题基础练习，有下列函数等内容，欢迎下载使用。

6.4用一次函数解决问题基础练习
一、单选题
1.等腰三角形的周长为20，设底边长为x，腰长为y，则y关于x的函数解析式为（x为自变量）（　　）
A. y＝20﹣x                      B. y＝20﹣2x                      C. y＝10﹣ 12 x                      D. y＝20﹣ 12 x
2.有下列函数：① y=x ，② y=4x ，③ y=−2x−3 ，④ y=1x+1−3 ，⑤ y=x2−1 ．其中是一次函数的有（   ）
A. 4 个                                     B. 3 个                                     C. 2 个                                     D. 1 个
3.如果每盒圆珠笔有12枝，售价18元，那么圆珠笔的销售额y(元)与圆珠笔的销售枝数x之间的函数关系式是(    )
A. y＝ 32 x                             B. y＝ 23 x                             C. y＝12x                             D. y＝ 112 x
4.鲁老师乘车从学校到省城去参加会议，学校距省城200千米，车行驶的平均速度为80千米/时．x小时后鲁老师距省城y千米，则y与x之间的函数关系式为（    ）

A. y=80x-200                    B. y=-80x-200                    C. y=80x+200                    D. y=-80x+200
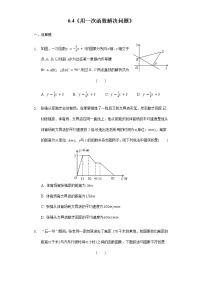
5.小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y（km）与已用时间x（h）之间的关系，则小敏、小聪行走的速度分别是（   ）

A. 3km/h和4km/h            B. 3km/h和3km/h            C. 4km/h和4km/h            D. 4km/h和3km/h
6.甲乙两名大学生去距学校36千米的某乡镇进行社会调查，他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车继续前往乡镇，乙骑电动车按原路返回．乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为x（分钟）．y甲、y乙与x之间的函数图象如图，则下列结论：①电动车的速度为0.9千米/分；②甲步行所用的时间为45分；③甲步行的速度为0.15千米/分；④乙返回学校时，甲与学校相距20千米．其中正确的个数是（   ）

A. 1个                                       B. 2个                                       C. 3个                                       D. 4个
7.使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施．某同学为了更加合理、科学、 节约的喷洒消毒液，做了如下的记录．壶中可装消毒液 400mL，喷壶每次放出 20mL 的水，壶里的剩余消毒液量 y（mL）与喷洒次数 n（次）有如下关系：
喷洒次数（n）
1
2
3
4
…
壶中剩余消毒液量（mL）
380
360
340
320
…
下列结论中正确的是（    ）
A. y 随 n 的增加而增大                                           B. 喷洒 10 次后，壶中剩余消毒液量为 0ml
C. y 与 n 之间的关系式为 y＝400﹣n                     D. 喷洒 18 次后，壶中剩余消毒液量为 40mL
8.已知汽车油箱内有油50L ， 每行驶100km耗油10L ， 那么汽车行驶过程中油箱内剩余的油量Q（L）与行驶路程S（km）之间的关系式是（　　）
A. Q＝50﹣ S100                   B. Q＝50+ S100                   C. Q＝50﹣ S10                   D. Q＝50+ S10
9.已知，如图，某人驱车在离A地10千米的P地出发，向B地匀速行驶，30分钟后离P地50千米，设出发x小时后，汽车离A地y千米（未到达B地前），则y与x的函数关系式为（　　）

A. y=50x                           B. y=100x                           C. y=50x-10                           D. y=100x+10
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝ 32 或t＝ 72 ，其中正确的结论有（   ）

A. 1个                                       B. 2个                                       C. 3个                                       D. 4个
二、填空题
11.已知等腰三角形的周长为60cm，若底边长为 y cm，一腰长为 x  cm.则 y 与 x  的函数关系式为      自变量 x 的取值范围是      
12.图书馆现有200本图书供学生借阅，如果每个学生一次借4本，则剩下的书y(本)和借书学生人数x(人)之间的关系式是________．
13.如果一盒圆珠笔有12支，售价24元，用y（元）表示圆珠笔的售价，x表示圆珠笔的支数，那么y与x之间的关系应该是________．
14.一名老师带领x名学生到青青世界参观，已知成人票每张60元，学生票每张40元设门票的总费用为y元，则y与x的关系式为       ．
15.在“抗疫”期间，某药店计划一次购进 A、B 两种型号的口罩共200盒，每盒A型口罩的销售利润为7.5元，每盒B型口罩的销售利润为10元，若要求B型口罩的进货量不超过A型口罩的3倍，且完全售出后利润不少于1870元，则该药店在此次进货中获得的最大利润是      元.
16.李庄与张庄两地之间的距离是100千米，若汽车以平均每小时80千米的速度从李庄开往张庄，则汽车距张庄的路程y（千米）与行驶时间x（小时）之间的函数关系式是       ．
17.在弹性限度内，弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数．一根弹簧不挂物体时长15 cm，当所挂物体的质量为5 kg时，弹簧长20 cm．当所挂物体质量为8kg时，弹簧的长度是      
18.某汽车生产厂对其生产的A型汽车进行耗油量实验，实验中汽车视为匀速行驶．

已知油箱中的余油量y（升）与行驶时间t（小时）的关系如下表，
行驶时间t（时）
0
1
2
3
油箱余油量y（升）
100
84
68
52
与行驶路程x（千米）的关系如图．则A型车在实验中的速度是      千米/时．
三、解答题
19.已知弹簧的长度y（厘米）在一定的限度内是所挂物质量x（千克）的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7. 2厘米,求这个一次函数的关系式．

20.甲、乙两人沿同一路线登山，图中线段OC、折线OAB分别是甲、乙两人登山的路程y（米）与登山时间x（分）之间的函数图象．请根据图象所提供的信息，解答如下问题：

（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量x的取值范围；
（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？

21.图①为汽车沿直线运动的速度v(m/s)与时间t(s)(0≤t≤40)之间的函数图象．根据对此图象的分析、理解，在图②中画出描述在这段时间内汽车离开出发点的路程s(m)与时间t(s)之间的函数图象．

22.如图，直线OB是一次函数y=2x的图象，点A的坐标是（0，2），点C在直线OB上且△ACO为等腰三角形，求C点坐标．


23.某校餐厅计划购买12张餐桌和一批餐椅，现从甲、乙两商场了解到：同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元．甲商场称：每购买一张餐桌赠送一把餐椅；乙商场规定：所有餐桌椅均按报价的八五折销售．那么，学校应如何购买更优惠？
24.如图，直线PA是一次函数y=x+1的图象，直线PB是一次函数y=﹣2x+2的图象．

（1）求A、B、P三点的坐标；
（2）求四边形PQOB的面积．
 
25.如图所示的图象反映的是：小明从家里跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家，其中x表示时间，y表示小明离家的距离．根据图象回答下列问题：

（1）体育场离小明家多远？小明从家到体育场用了多少时间？
（2）体育场离文具店多远？
（3）小明在文具店逗留了多少时间？
（4）小明从文具店回家的平均速度是多少？
26.某学校计划购买3至8台电脑，现从甲、乙两家商场了解到同一型号电脑每台报价均为6000元，并且多买都有一定的优惠，各商场的优惠条件如下表所示：
商场
优惠条件
甲商场
第一台按原报价收费，其余每台优惠25%
乙商场
每台优惠20%
该学校选择哪家商场购买更优惠．
27.我县为了倡导居民节约用水，生活用水按阶梯式水价计费，如图是居民每户每月的水费y(元)与所用的水量x（吨）之间的函数图象，请根据图象所提供的信息，解答下列问题：


（1）当用水量不超过10吨时，每吨水收费多少元？

（2）当用水量超过10吨且不超过30吨时，求y与x之间的函数关系式；

（3）某户居民三、四月份水费共82元，四月份用水比三月份多4吨，求这户居民三月份用水多少吨。

28.台州市某体育用品商店一次性购进排球、足球两种商品共100个，排球每个进价40元，售价50元，足球每个进价90元，售价105元.

（1）设购进排球x个，销售完此两种商品的总利润为y元，求出y与x的函数关系式；

（2）该商家计划最多投入8000元用于购进此两种商品共100件，至少要购进多少个排球？

（3）在（2）的条件下，若售完这些商品，商家可获得最大利润是多少元？


答案解析部分
一、单选题
1.【答案】 B
【考点】根据实际问题列一次函数表达式
【解析】【解答】解：底边长y关于腰长x的函数解析式是y＝-2x+20.
故答案为：B.
【分析】根据三角形周长分公式可得x+2y=20，整理即可得到y关于x的函数.
2.【答案】 C
【考点】根据实际问题列一次函数表达式
【解析】【解答】∵形如 y=kx+b(k≠0) 时， y 为 x 的一次函数，
∴①③符合题意．
故答案为：C.
【分析】根据一次函数表达式，可知①③符合题意，故正确选项为C
3.【答案】 A
【考点】根据实际问题列一次函数表达式
【解析】【解答】 y=1812x=32x ，
故答案为：A.
【分析】根据圆珠笔的销售额=单价×销量，即可求出结论.
4.【答案】 D
【考点】根据实际问题列一次函数表达式
【解析】【解答】依题意有y=200-80x=-80x+200．
故答案为：D．
【分析】由题意可得y=学校与省城的距离-汽车行驶的路程即可求解。
5.【答案】 D
【考点】一次函数的实际应用
【解析】【解答】解：设小敏的速度为：m，则函数式为，y=mx+b，
由已知小敏经过两点（1.6，4.8）和（2.8，0），
所以得：4.8=1.6m+b，0=2.8m+b，
解得：m=﹣4，b=11.2，
小敏离B地的距离y（km）与已用时间x（h）之间的关系为：y=﹣4x+11.2；
由实际问题得小敏的速度为4km/h．
设小聪的速度为：n，则函数图象过原点则函数式为，y=nx，
由已知经过点（1.6，4.8），
所以得：4.8=1.6n，
则n=3，
即小聪的速度为3km/h．
故选D．
【分析】由已知图象上点分别设出两人的速度，写出函数关系式，求出两人的速度．
6.【答案】 C
【考点】一次函数的实际应用
【解析】【解答】解：①由图象，得
18÷20=0.9，故①说法正确；②乙从学校追上甲所用的时间为：（36﹣13.5）÷0.9=25分钟，
∴甲步行所用的时间为：20+25=45分钟，故②书法正确；③由题意，得
甲步行的速度为：（36﹣13.5﹣18）÷45=0.1千米/分，故③说法错误；④乙返回到学校时，甲与学校的距离为：18+0.1×20=20千米，故④说法正确；
故答案为：C．
【分析】根据图像求出电动车的速度，求出从学校追上甲所用的时间，得到甲步行所用的时间，求出甲步行的速度，求出乙返回到学校时，甲与学校的距离；判断即可.
7.【答案】 D
【考点】一次函数的实际应用
【解析】【解答】解：A、由题意可知y随n的增大而减小，故本选项不符合题意；
B、喷洒 10 次后，壶中剩余消毒液量为200ml，故本选项不符合题意；
C、根据题意可得y＝400﹣20n，故本选项不符合题意；
D、放水时间18分钟，壶中剩余消毒液量为 40ml，故本选项符合题意；
故答案为：D．
【分析】根据题意可得蓄水量y＝400﹣20n，从而进行各选项的判断即可．
8.【答案】 C
【考点】根据实际问题列一次函数表达式
【解析】【解答】解：汽车单位耗油量为10÷100＝ 0.1 L ，
∴行驶S千米的耗油量为 0.1 SL ，
∴Q＝50﹣ 0.1 S＝50﹣ S10 ，
故答案为：C ．
【分析】根据剩余油量等于总油量减去消耗的油量列等量关系式即可。
9.【答案】 D
【考点】根据实际问题列一次函数表达式
【解析】【解答】∵汽车在离A地10千米的P地出发，向B地匀速行驶，30分钟后离P地50千米（未到达B地前），
∴汽车的速度=50÷0.5=100（千米/时），
则依题意有：y=100x+10
选：D．
【分析】根据汽车的速度=50÷0.5=100千米/时，汽车离A地距离=10+行驶距离得出
10.【答案】 A
【考点】一次函数的实际应用
【解析】【解答】解：由图象可知A、B两城市之间的距离为300km，故①正确；
甲行驶的时间为5小时，而乙是在甲出发1小时后出发的，且用时3小时，即比甲早到1小时，故②错误；
设甲车离开A城的距离y与t的关系式为y甲＝kt，
把（5，300）代入可求得k＝60，
∴y甲＝60t，
把y＝150代入y甲＝60t，可得：t＝2.5，
设乙车离开A城的距离y与t的关系式为y乙＝mt+n，
把（1，0）和（2.5，150）代入可得 {m+n=02.5m+n=150 ，解得 {m=100n=−100 ，
∴y乙＝100t﹣100，
令y甲＝y乙可得：60t＝100t﹣100，解得t＝2.5，
即甲、乙两直线的交点横坐标为t＝2.5，
此时乙出发时间为1.5小时，即乙车出发1.5小时后追上甲车，故③错误；
令|y甲﹣y乙|＝40，可得|60t﹣100t+100|＝40，即|100﹣40t|＝40，
当100﹣40t＝40时，可解得t＝ 32 ，
当100﹣40t＝﹣40时，可解得t＝ 72 ，
又当t＝ 23 时，y甲＝40，此时乙还没出发，
当t＝ 133 时，乙到达B城，y甲＝260；
综上可知当t的值为 32 或 72 或 23 或t＝ 133 时，两车相距40千米，故④不正确；
故答案为：A.
【分析】由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式，可求得两函数图象的交点，进而判断，再令两函数解析式的差为40，可求得t，可得出答案.
二、填空题
11.【答案】 y=60-2x；(15﹤x﹤30)
【考点】根据实际问题列一次函数表达式
【解析】【解答】依题意得y+2x=60，即y=60-2x（15＜x＜30）．
【分析】根据三角形的周长=三角形的三边之和可得60=y+2x，变形得，y=60-2x（15＜x＜30）。
12.【答案】 y＝200－4x(0≤x≤50的整数)
【考点】根据实际问题列一次函数表达式
【解析】【解答】解：y＝200－4x(0≤x≤50的整数).
故答案为：y＝200－4x(0≤x≤50的整数).
【分析】根据数量关系：剩下的图书本数＝图书总本数-借出的图书本数，即可列出函数关系式.
13.【答案】 y＝2x
【考点】根据实际问题列一次函数表达式
【解析】【解答】解：∵一盒圆珠笔有12支，售价24元，
∴每只平均售价为2元，
∴y与x之间的关系是：y＝2x．
故答案为：y＝2x．
【分析】利用24÷12=2求出圆珠笔每只平均售价，利用总售价=单价×数量即得结论.
14.【答案】 y=60+40x
【考点】根据实际问题列一次函数表达式
【解析】【解答】依等量关系式“总费用＝老师费用＋学生费用”可得： y=60+40x ．
故答案是： y=60+40x ．

【分析】本题考查学生解决实际问题的能力，根据题目的等量关系列方程即可，难度较小
15.【答案】 1875
【考点】一次函数的实际应用
【解析】【解答】解：A型口罩购买m盒，则B型口罩购买（200-m）盒，
依题意，得：
{200−m≤3m7.5m+10(200−m)≥1870 ，
解得：50≤m≤52.
设销售总利润为w元，则w=7.5m+10(200-m)=-2.5m+2000，
∵k=-2.5＜0，
∴w随m的增大而减小，
∴当m=50时，w取得最大值，
∴购买A型口罩50盒，B型口罩150盒时，完全售出后获得的利润最大，最大值为w=-2.5 ×50 +2000=1875(元).
故答案为：1875.
【分析】设A型口罩购买m盒，则B型口罩购买（200-m）盒，根据“B型口罩的进货量不超过A型口罩的3倍，且完全售出后利润不少于1870元”，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，设销售总利润为w元，根据总利润=每盒利润×销售数量（购买数量），即可得出w关于m的函数关系式，再利用一次函数的性质即可解决最值问题.
16.【答案】 y＝100﹣80x
【考点】根据实际问题列一次函数表达式
【解析】【解答】解：∵汽车的速度是平均每小时80千米，
∴他行驶x小时走过的路程是80x ，
∴汽车距张庄的路程y=100－80x ．
故填y=100－80x ．

【分析】汽车距张庄的路程=总路程-走过的路程，根据题意写出函数关系即可。
17.【答案】 23 cm
【考点】一次函数的实际应用
【解析】【解答】设y与x的函数关系式y=kx+15（k≠0），
当x=5时，y=20，
∴5k+15=20，解得k=1，
∴y=x+15，
当x=8时，y=8+15=23,
∴ 当所挂物体质量为8kg时，弹簧的长度是23cm.
【分析】先求出y与x的函数解析式，再求出x=8时的y值即可.
18.【答案】 100
【考点】一次函数的实际应用
【解析】【解答】设油箱中的余油量y与行驶路程x（千米）的函数关系为y=kx+b，
由题意得
b=100,20=500k+b，
解之得b=100，k=-0.16，
∴y=-0.16x+100，
设油箱中的余油量y（升）与行驶时间t（小时）的函数关系为y=kt+b，
由题意得
b=100
84=k+b，
解之得b=100，k=-16，
∴y=-16t+100，
当y=50时，x= 500.16 ，t= 5016 ，
∴速度v= 500.16 ÷ 5016 =100千米/时．
故答案为：100
【分析】根据图形信息把两点坐标代入，求出油箱中的余油量y与行驶路程x（千米）的函数关系，再由表格信息求出油箱中的余油量y（升）与行驶时间t（小时）的函数关系，求出路程和时间，求出速度.
三、解答题
19.【答案】 设所求函数的关系式是y=kx+b，
根据题意，得b=64k+b=7.2
解这个方程组，得b=6k=0.3
所以所求函数的关系式是y=0.3x+6

【考点】根据实际问题列一次函数表达式
【解析】【分析】已知所求函数为一次函数，可以设所求函数的关系式是y=kx+b，再由题中的已知条件代入上式，求出k、b的值，代入y=kx+b，即可求的这个一次函数的关系式．

20.【答案】 解：（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，

∵点C（30，600）在函数y=kx的图象上，
∴600=30k，
解得k=20，
∴y=20x（0≤x≤30）；
（2）设乙在AB段登山的路程y与登山时间x之间的函数解析式为y=ax+b（8≤x≤20），
由图形可知，点A（8，120），B（20，600）
所以，8a+b=12020a+b=600 ，
解得a=40b=-200 ，
所以，y=40x﹣200，
设点D为OC与AB的交点，
联立y=20xy=40x-200 ，
解得x=10y=200 ，
故乙出发后10分钟追上甲，此时乙所走的路程是200米．

【考点】一次函数的实际应用
【解析】【分析】（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，根据图象得到点C的坐标，然后利用待定系数法求一次函数解析式解答；

（2）根据图形写出点A、B的坐标，再利用待定系数法求出线段AB的解析式，再与OC的解析式联立求解得到交点的坐标，即为相遇时的点．
21.【答案】 解：根据图①的信息，
从0秒到20秒，时间为20 s，速度为10 m/s，
则离开出发点的路程为 10×20=200 (m)；
从20秒到30秒，时间为10 s，速度为0 m/s，
则离开出发点的路程还是 200 (m)；
从30秒到40秒，时间为10 s，速度为20 m/s，
则离开出发点的路程是 200+20×10=400 (m)；
∴这段时间内汽车离开出发点的路程s(m)与时间t(s)之间的函数图象如图所示：

【考点】一次函数的实际应用
【解析】【分析】根据时间与速度的乘积等于路程求出各段的路程，即可画出图形．
22.【答案】 解：若此等腰三角形以OA为一腰，且以A为顶点，则AO=AC1=2．

设C1（x，2x），则得x2+（2x﹣2）2=22 ，
解得x=85 ， 得C1（85,165），
若此等腰三角形以OA为一腰，且以O为顶点，则OC2=OC3=OA=2，
设C2（x′，2x′），则得x′2+（2x′）2=22 ， 解得x'=45=255 ，
∴C2（255,455），
又由点C3与点C2关于原点对称，得C3（-255,-455），
若此等腰三角形以OA为底边，则C4的纵坐标为1，从而其横坐标为12 ， 得C4（12,1），
所以，满足题意的点C有4个，坐标分别为：（85,165），（255,455），（-255,-455），C4（12,1）．

【考点】一次函数的实际应用
【解析】【分析】本题要分三种情况进行讨论，

第一种情况：以OA为腰，A为等腰三角形的顶点，那么C点必定在第一象限，且纵坐标的值比A的要大，根据OA=AC我们知道了AC的距离，我们可以根据C的纵坐标和横坐标以及AC的长构成的直角三角形，运用勾股定理以及所在直线的函数关系式求出C的坐标．
第二种情况：以OA为一腰，O为三角形的顶点，那么C点可以有两个，一个在第一象限，一个在第三象限，且这两个点关于原点对称．我们只要求出一个两个就都求出来了，求的方法同第一种情况．
第三种情况：以OA为底，OC，AC为腰，此点在第一象限，那么这点的纵坐标必为1（顶点在底边的垂直平分线上），那么根据所在函数的关系式，可求出这个C点的坐标．
23.【答案】 解：设学校购买12张餐桌和 x 把餐椅，到购买甲商场的费用为 y1 元，到乙商场购买的费用为 y2 元，则有
y1=200×12+50(x−12)=50x+1800
y2=85％×(200×12+50x)=42.5x+2040
y1−y2=7.5x−240
当 7.5x−240