

苏科版八年级上册6.1 函数课堂检测
展开
第6章一次函数6.1--6.3基础练习
一、单选题
1.在平面直角坐标系 xOy 中,下列函数的图象不过点 (1,1) 的是( )
A. y=1x B. y=x2 C. y=−x+1 D. y=x3
2.已知一次函数 y=(3−2k)x+6 ( k 为常数)的图象经过 A(x1,y1) , B(x2,y2) ,若 x1>x2 , y1
3.下列一次函数中,y随x的增大而减小的是( )
A. y=10x+4 B. y=x-3 C. y=-2x D. y=0.3x
4.点(a,﹣1)在一次函数y=﹣2x+1的图象上,则a的值为( )
A. a=﹣3 B. a=﹣1 C. a=1 D. a=2
5.下图中,不是函数图象的是( )
A. B.
C. D.
6.一次函数 y=(m−2)x+m+3 的图象如图所示,则m的取值范围是( )
A. m>2 B. m<2 C. 2<m<3 D. -3<m<2
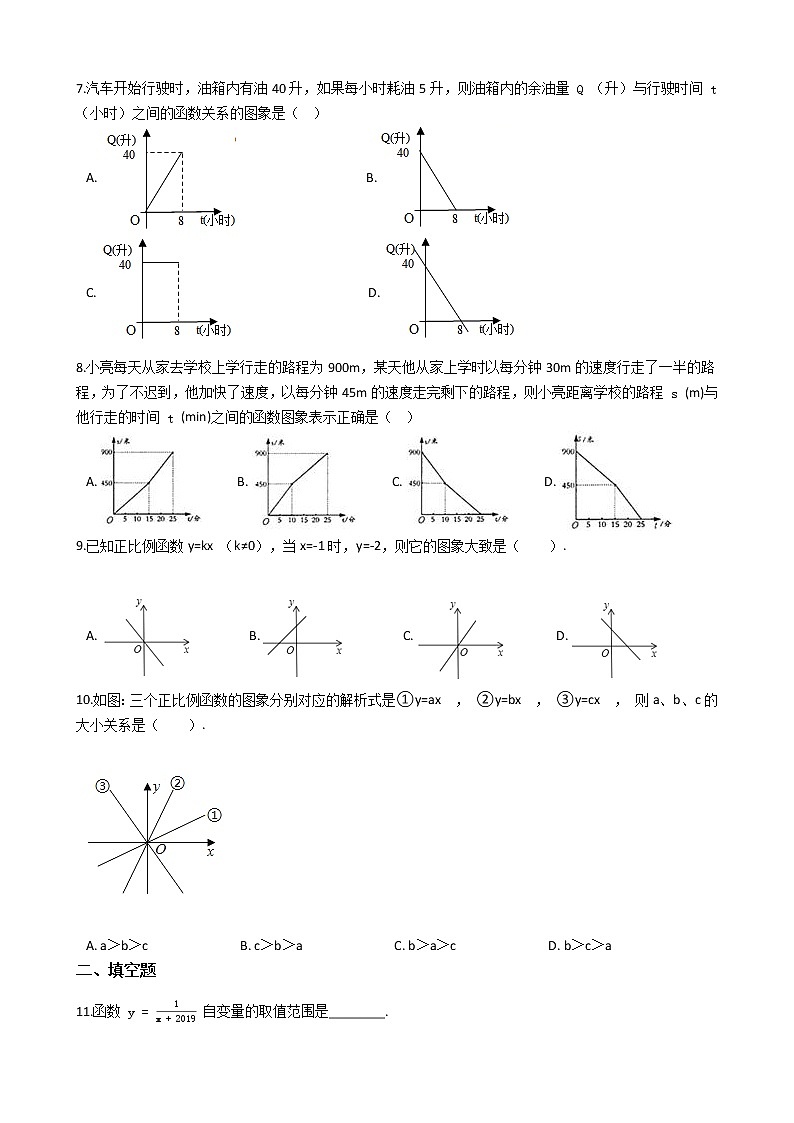
7.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量 Q (升)与行驶时间 t (小时)之间的函数关系的图象是( )
A. B.
C. D.
8.小亮每天从家去学校上学行走的路程为900m,某天他从家上学时以每分钟30m的速度行走了一半的路程,为了不迟到,他加快了速度,以每分钟45m的速度走完剩下的路程,则小亮距离学校的路程 s (m)与他行走的时间 t (min)之间的函数图象表示正确是( )
A. B. C. D.
9.已知正比例函数y=kx (k≠0),当x=-1时,y=-2,则它的图象大致是( ).
A. B. C. D.
10.如图:三个正比例函数的图象分别对应的解析式是①y=ax , ②y=bx , ③y=cx , 则a、b、c的大小关系是( ).
A. a>b>c B. c>b>a C. b>a>c D. b>c>a
二、填空题
11.函数 y=1x+2019 自变量的取值范围是________.
12.已知点 P(a,−3) 在一次函数 y=2x+9 的图象上,则 a= ________.
13.已知一次函数y=kx+b(k、b为常数,且k≠0),x、y的部分对应值如下表:
x
…
-2
-1
0
1
…
y
…
0
-2
-4
-6
…
当y>0时, x 的取值范围是
14.若一次函数y=(a﹣2)x+(a+2)经过第一、二、四象限,则a的取值范围为 .
15.日出日落,一天的气温随时间的变化而变化,在这一问题中,自变量是
16.如图,已知一次函数y=kx+b的图象,且y>0,则x的取值范围是 .
17.如图1,正方形ABCD中,点P从点A出发,以每秒2厘米的速度,沿A→D→C方向运动,点Q从点B出发,以每秒1厘米的速度,沿BA向点A运动,P、Q同时出发,当点P运动到点C时,两动点停止运动,若△PAQ的面积y(cm2)与运动时间x(s)之间的函数图象为图2,若线段PQ将正方形分成面积相等的两部分,则x的值为________ .
18.林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中元/升是常量, 是变量。
三、解答题
19.已知一次函数 y=(2m−2)x+m+1 中,y随x的增大而减小,且其图象与y轴交点在x轴上方.求m的取值范围.
20.已知正比例函数y=(m+2)x中,y的值随x的增大而增大,而正比例函数y=(2m-3)x , y的值随x的增大而减小,且m为整数,你能求出吗?为什么?
21.已知函数 y=(m+2)xm2−3+m−2 是一次函数,求m的值.
22.填表,并在同一坐标系内作出函数y=2x-5 和y=-x+1的图像;
填表:y=2x-5
x
…
0
…
y
…
0
…
y=-x+1
x
…
0
…
y
…
0
…
23.写出下列函数关系式,并指出关系式中的自变量和函数:
圆锥的底面半径为定值r,则圆锥的体积V与圆锥的高h之间的关系.
24.已知正比例函数y=(m﹣1)x5-m2的图象在第二、四象限,求m的值.
25.下表是达州某电器厂2014年上半年每个月的产量:
x/月
1
2
3
4
5
6
y/台
10000
10000
12000
13000
14000
18000
(1)根据表格中的数据,你能否根据x的变化,得到y的变化趋势?
(2)根据表格你知道哪几个月的月产量保持不变?哪几个月的月产量在匀速增长?哪个月的产量最高?
(3)试求2014年前半年的平均月产量是多少?
26.已知点P(m,n)在一次函数y=2x﹣3的图象上,且m>2n,求m的取值范围.
27.已知一次函数y=(2m+4)x+(3-n).当m、n是什么数时,y随x的增大而增大.
28.已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2007的值.
答案解析部分
一、单选题
1.【答案】 C
【考点】函数的图象
【解析】【解答】解:当x=1时, y=1x=11=1 , y=1x 图象过点 (1,1) ,选项A不合题意;
当x=1时, y=12=1 , y=x2 图象过点 (1,1) ,选项B不合题意;
当x=1时, y=−1+1=0 , y=−x+1 图象不过点 (1,1) ,选项C合题意;
当x=1时, y=13=1 , y=x3 图象过点 (1,1) ,选项D不合题意;
故答案为:C.
【分析】把点(1,1)分别代入解析式判断即可。
2.【答案】 D
【考点】一次函数的性质
【解析】【解答】解:∵ y=(3−2k)x+6 的图象经过点A(x1 , y1)和点B(x2 , y2),当x1>x2时,y1<y2 ,
∴y随x的增大而减小,
∴3-2k<0.
解得: k>32
故答案为:D.
【分析】由题意可得:y随x的增大而减小,故该函数自变量的系数应该小于0,据此列出不等式,求解就可得到k的范围.
3.【答案】 C
【考点】一次函数的性质
【解析】【解答】解:在y=10x+4、y=x-3和y=0.3x中
k分别为10,1,0.3,y随x的增大而增大;
在y=-2x中,k=-2,y随x的增大而减小.
故答案为:C.
【分析】形如“y=kx+b(k,b为常数,且k≠0)”的函数就是一次函数,一次函数中k大于0的时候,y随x的增大而增大;k小于0的时候,y随x的增大而减小,从而即可一一判断得出答案.
4.【答案】 C
【考点】一次函数的性质
【解析】【解答】解:∵点(a,﹣1)在一次函数y=﹣2x+1的图象上,
∴﹣1=﹣2a+1,
解得a=1,
故答案为:C.
【分析】将点(a,﹣1)代入一次函数解析式即可求解.
5.【答案】 B
【考点】函数的图象
【解析】【解答】解:由函数的定义可知,对于每一个自变量的x的取值,都有唯一的y值与其对应,选项B中当x取一个正数时,有两个y值与其对应,故答案为:B中的图象不是函数图象,而其它选项中,对于每一个自变量的x的取值,都有唯一的y值与其对应,故是函数图象,
故答案为:B.
【分析】设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量.根据函数的定义和函数图象可以判断哪个选项中的图象不是函数图象.
6.【答案】 D
【考点】一次函数的图象
【解析】【解答】解:如图所示,一次函数y=(m−2)x+3的图象经过第一、二、四象限,
∴m−2<0且m+3>0,
解得:-3<m<2.
故答案为:D.
【分析】先求出m−2<0且m+3>0,再解不等式求解即可。
7.【答案】 B
【考点】函数的图象
【解析】【解答】解:由题意得,油箱内余油量Q(升)与行驶时间t(小时)的关系式为:
Q=40-5t(0≤t≤8),
结合解析式可得出图象:
故答案为:B.
【分析】根据油箱内余油量=原有的油量-t小时消耗的油量,可列出函数关系式,得出图象.
8.【答案】 D
【考点】函数的图象
【解析】【解答】小亮距离学校的路程 s (米)应随他行走的时间t(分)的增大而减小,因而选项A.B一定不符合题意;
他从家去上学时以每分30米的速度行走了450米,所用时间应是15分钟,因而选项C不符合题意;
行走了450米,为了不迟到,他加快了速度,后面一段图象陡一些,选项D符合题意.
故答案为:D.
【分析】根据行程,按照路程的一半分段,先慢后快,图象先平后陡.
9.【答案】 C
【考点】正比例函数的图象和性质
【解析】【解答】将x=-1,y=-2代入正比例函数y=kx (k≠0)得,
-2=-k ,
k=2>0,
∴函数图象过原点和一、三象限
选:C.
【分析】将x=-1,y=-2代入正比例函数y=kx (k≠0),求出k的值,即可根据正比例函数的性质判断出函数的大致图象
10.【答案】 C
【考点】正比例函数的图象和性质
【解析】【解答】首先根据图象经过的象限,得a>0,b>0,c<0,
再根据直线越陡,|k|越大,则b>a>c
选:C.
【分析】根据正比例函数图象的性质分析
二、填空题
11.【答案】 x≠-2019
【考点】函数自变量的取值范围
【解析】【解答】根据题意若函数 y=1x+2019 有意义,
可得x+2019≠0;
解得x≠-2019.
所以答案是:x≠-2019.
【分析】因为分式有意义的条件是分母不为0,所以可得关于x的不等式,x+2019≠0;解不等式即可求解。
12.【答案】 -6
【考点】一次函数的图象
【解析】【解答】∵点P(a,-3)在一次函数y=2x+9的图象上,
∴ 2a+9=−3 ,解得: a=−6 .
故答案为: −6 .
【分析】把点P的坐标代入一次函数的解析式,即可求出答案.
13.【答案】 x<-2
【考点】函数值
【解析】【解答】解:当x=﹣2时,y=0,根据表可以知道函数值y随x的增大而减小,∴y>0时,x的取值范围是x<﹣2.
故答案为:x<﹣2.
【分析】先根据所给函数图像上点的坐标判断一次函数的增减性,从而易得y>0时x的取值范围.
14.【答案】 ﹣2<a<2
【考点】一次函数图象、性质与系数的关系
【解析】【解答】解:∵一次函数y=(a﹣2)x+(a+2)经过第一、二、四象限,
∴ {a−2<0a+2>0 ,
∴﹣2<a<2.
故答案为﹣2<a<2.
【分析】利用一次函数与系数的关系得到 {a−2<0a+2>0 ,然后解不等式组即可.
15.【答案】 时间
【考点】常量、变量
【解析】【解答】解:日出日落,一天的气温随时间的变化而变化,
温度随时间的变化而变化,气温是时间的函数,时间是自变量,
故答案为:时间.
【分析】根据温度随时间的变化而变化,可得答案.
16.【答案】 x<3
【考点】一次函数图象、性质与系数的关系
【解析】【解答】x轴上方的函数图象所对应的自变量的取值为x<3.
故答案为x<3
【分析】由已知y>0可知,直线在x轴的上方,而直线与x轴相较于(3,0),所以可得x的取值范围为x<3.
17.【答案】 3
【考点】函数的图象
【解析】【解答】解:设正方形的边长为acm,由题意知,点P的运动路程为2xcm,BQ=xcm,
当0<x≤a2时,y=12•AQ•AP=12(a﹣x)•2x=﹣x2+ax=﹣(x﹣a2)2+a24 ,
则当x=时,y取得最大值,最大值为a24 ,
由题意可知,a24=9,解得:a=6或a=﹣6(舍),
当y=9时,x=a2=3,
故答案为:3.
【分析】由题意可知,当点P在AD上运动时y与x满足二次函数关系,当点P在DC上运动时y与x满足一次函数关系,设正方形的边长为acm,列出当0<x≤a2时y与x的函数关系式并配方,结合函数图象可得a的值,进而求出此时x的值.
18.【答案】 数量、金额
【考点】常量、变量
【解析】【解答】在这三个量当中元/升是常量,数量、金额是变量
【分析】常量就是在变化过程中不变的量,变量是指在程序的运行过程中随时可以发生变化的量
三、解答题
19.【答案】 解:∵一次函数y随x的增大而减小∴ 2m−2<0m<1 又∵其图象与y轴交点在x轴上方m+1>0∴m>−1 ∴m的取值范围是: −1
【解析】【分析】一次函数中,y随x增大而减小,说明自变量系数小于0,即2m-2<0,图象过二、四象限;又该函数的图象与y轴交点在x轴上方,据此解答m的取值范围即
20.【答案】 解:m的可能值为-1,0,1.理由如下:∵正比例函数y=(m+2)x中,y的值随x的增大而增大,∴m+2>0,解得m>-2.∵正比例函数y=(2m-3)x,y的值随x的增大而减小,∴2m-3<0,解得m<1.5.∵m为整数,∴m的可能值为-1,0,1
【考点】正比例函数的图象和性质
【解析】【分析】根据已知条件和正比例函数的性质可得m+2>0,2m-3<0,解这个不等式组可求m的可能值。
21.【答案】 解:∵函数 y=(m+2)xm2−3+m−2 是一次函数,
∴m+2≠0且m2-3=1,
解得:m=2,
【考点】一次函数的定义
【解析】【分析】一次函数要求自变量x前的系数不等于0,指数是1,据此即可解题.
22.【答案】 解:当x=0时,y=2×0-5=-5,当y=0时,0=2x-5,x=2.5;当x=0代入y=0+1=1,当y=0时,0=-x+1,x=1。填表如下:
x
…
0
2.5
…
y
…
-5
0
…
x
…
0
1
…
y
…
1
0
…
过点(0,-5),(2.5,0)画直线,可得函数y=2x-5的图象;过点(0,1),(1,0)画直线,可得函数y=-x+1的图象。如下图:
【考点】一次函数的图象
【解析】【分析】本题考查了一次函数的图象性质,一次函数图象上点的坐标特征及图象的画法,是基础知识,需熟练掌握。
23.【答案】 解:圆锥的体积公式为:V= 13 πr2h,
∴圆锥的体积V与圆锥的高h之间的函数关系式为:V= 13 πr2h,
函数自变量为h,V为自变量h的函数
【考点】函数解析式
【解析】【分析】由圆锥的体积公式即可写出函数关系式,然后再确定自变量和函数即可.
24.【答案】 解:∵正比例函数y=(m﹣1)x5-m2 , 函数图象经过第二、四象限,
∴m﹣1<0,5﹣m2=1,
解得:m=﹣2.
【考点】一次函数的定义
【解析】【分析】当一次函数的图象经过二、四象限可得其比例系数为负数,据此求解.
25.【答案】 解:(1)随着月份x的增大,月产量y正在逐渐增加;
(2)1月、2月两个月的月产量不变,3月,4月、5月三个月的产量在匀速增多,
6月份产量最高;
(3)2014年前半年的平均月产量:
(10000+10000+12000+13000+14000+18000)÷6≈12833(台).
【考点】函数的表示方法
【解析】【分析】(1)根据表格数据可得y随x的增大而增大;
(2)根据表格数据可得1、2月份的月产量均为10000,保持不变;3月,4月、5月三个月的产量在匀速增多,每月增加1000台,6月份产量最高;
(3)前半年的平均月产量把1到6月份的总产量除以6即可.
26.【答案】 解: ∵ 点P(m,n)在一次函数y=2x﹣3的图象上,
∴n=2m−3,
∵ m>2n,
∴m > 2(2m−3),
∴m > 4m−6,
∴3m < 6,
∴m < 2.
【考点】解一元一次不等式,一次函数的图象
【解析】【分析】由点P(m,n)在一次函数y=2x﹣3的图象上,可得 n=2m−3, 再代入不等式m>2n,解不等式后可得答案.
27.【答案】 解答: 2m+4>0,即m>-2,n为任何实数时,y随x的增大而增大.
【考点】一次函数的性质
【解析】【分析】由一次函数图象的性质解答
28.【答案】 解答:由题意得:|k|=1且k-1≠0,解得:k=-1,(3k+2)2007=(-3+2)2007=-1
【考点】一次函数的定义
【解析】【分析】首先根据一次函数定义确定k的值,再代入代数式(3k+2)2007求值.
苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课堂检测: 这是一份苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课堂检测,共16页。试卷主要包含了5-6,一次函数,直线 ,如图,直线L1,如图,直线y1=kx+b过点A等内容,欢迎下载使用。
初中数学苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式同步练习题: 这是一份初中数学苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式同步练习题,共21页。试卷主要包含了5-6,如图,直线y=kx+3经过点,直线 l1,已知直线 l1 等内容,欢迎下载使用。
苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课后复习题: 这是一份苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式课后复习题,共19页。试卷主要包含了5-6等内容,欢迎下载使用。













