高中数学一轮专题-九月数学试卷

这是一份高中数学一轮专题-九月数学试卷，共4页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
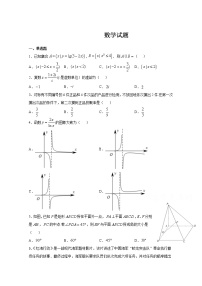
九月数学试卷姓名：___________班级：___________分数：___________第I卷 选择题部分（共60分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合,或，则（    ）A． B．C． D．2．设函数，则等于（    ）A． B．1 C． D．53．下列命题中正确的是（    ）A．，               B．，C．，       D．，4．设函数在定义域内可导，的图象如图所示，则导函数的图象为（    ）A． B．C． D．5. 函数在区间上的最大值是（    ）A． B． C． D．6．设，，，则（    ）A． B． C． D．7．已知，在第二象限内，那么的值等于（    ）A． B． C． D．以上都不对8．若函数在区间内存在单调递增区间，则实数的取值范围是（  ）A． B． C． D． 二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得2分，有选错的得0分.9．已知定义在上的函数满足，则下列式子成立的是（    ）A． B．C．是上的增函数 D．若，则有10．如图是函数的部分图象，下列选项正确的是（    ）A． B．C． D．11．已知函数在区间上有最小值，则函数在区间上一定（    ）A．是奇函数 B．是增函数 C．无最值 D．有最大值12．已知函数是定义在上的奇函数，当时，.则下列结论正确的是（    ）A．当时，B．函数在上有且仅有三个零点C．若关于的方程有解，则实数的取值范围是D．，第II卷 非选择题部分（共90分）三、填空题：本大题共4小题，每小题5分，共20分.13．已知函数的导函数为，且满足关系式，则的值等于__________.14．函数的部分图象如图所示，则的单调递增区间为___________．15．经过原点作函数图像的切线，则切线方程为__________．16．设函数是定义在上的偶函数，且对任意的恒有，已知当时，，则下列命题：①对任意，都有；     ②函数在上递减，在上递增；③函数的最大值是1，最小值是0；       ④当时，.其中正确命题的序号有_________.四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．已知（）在处取得极值.（1）求实数的值；（2）求的单调区间；          18．已知，()（1）当时，若和均为真命题，求的取值范围：（2）若是的充分不必要条件，求的取值范围．          19. 已知函数，先将的图象向左平移个单位长度后，再将所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数的图象.（1）当时，求函数的值域；（2）求函数在上的单调递增区间.         20．设函数．（1）求函数的单调区间．（2）若方程有且仅有三个实根，求实数的取值范围．            21．已知函数是定义在上的减函数，且满足，．（1）求；（2）若，求的取值范围．         22．已知函数(其中)，为的导数.（1）求导数的最小值；（2）若不等式恒成立，求的取值范围.