高中数学人教版新课标B必修12.1.3函数的单调性背景图课件ppt

这是一份高中数学人教版新课标B必修12.1.3函数的单调性背景图课件ppt，共12页。PPT课件主要包含了自学提纲，增区间-∞+∞等内容，欢迎下载使用。

1、什么叫做增函数（减函数）？ 什么叫做单调性？单调区间？
2、如何判断或证明函数的单调性？
如果一个函数在某个区间M上是增函数或是减函数，就说这个函数在这个区间M上具有单调性。（区间M称为单调区间）
判断下列两个命题的正误：1、已知f(x)是[a,b]上增函数，若存在x1,x2∈[a,b]且x2-x1>0，则 f(x2)-f(x1)>0。2、已知f(x)是[a,b]上增函数，若存在x1,x2∈[a,b]且f(x1)-f(x2)>0，则 x2-x1>0。3、若存在x1,x2∈[a,b]且x1说明： 1、x1,x2必须同属于一个单调区间； 2、“任意”两个字不能去掉，不能用特殊值替换； 3、x1,x2必须有大小，通常规定X2-x1>0。
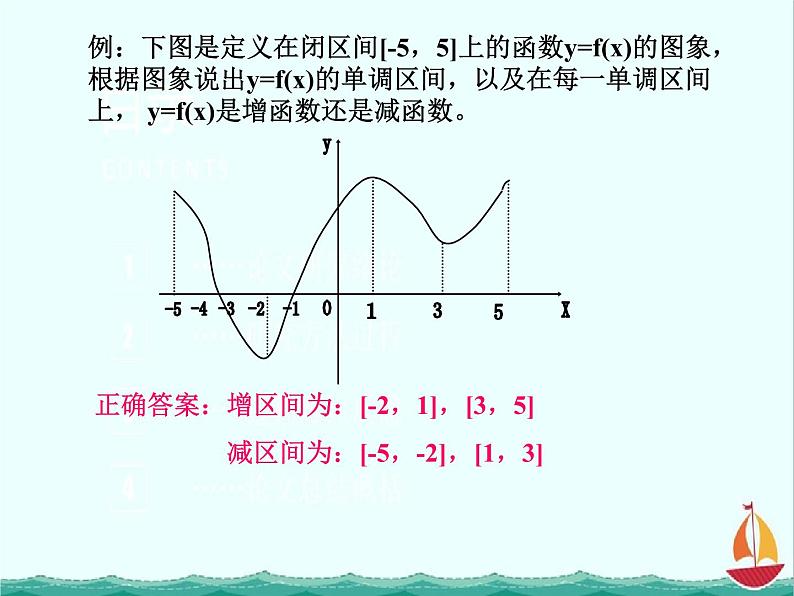
例：下图是定义在闭区间[-5，5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一单调区间上， y=f(x)是增函数还是减函数。
正确答案：增区间为：[-2，1]，[3，5] 减区间为：[-5，-2]，[1，3]
正确答案：增区间：[-2，1]，[3，5]减区间：[-5，-2]，[1，3]
增区间：[-2，1]，[3，5]减区间：[-5，-2]，[1，3]
增区间：[-2，0]，（0，1]， [3，5]减区间：[-5，-2]，[1，3]
练习1：根据下列函数图象，写出其单调区间。
正确答案：增区间（-∞，0]， 减区间 [0，+∞）
减区间（-∞，0），　　　 （0，+∞）
证明函数f(x)=kx+b(k>0) 在(-∞,+∞）上是增函数。
注意：我们在证明函数的单调性时，不能“以图代证”，而是严格按照定义证明
回想一下，定义的本质是什么？仿照例题，本题怎么用定义证明？
P46探索与研究习题（重点证明过程）
一般地，设函数y=f(x)的定义域为A,区间M A.如果取区间M中的任意两个值x1、x2,改变量 ，则当 时，就称函数y=f(x)在区间M上是增函数，当 时，就称函数y=f(x)在区间M上是减函数。