





高中2.1.1函数教课内容课件ppt
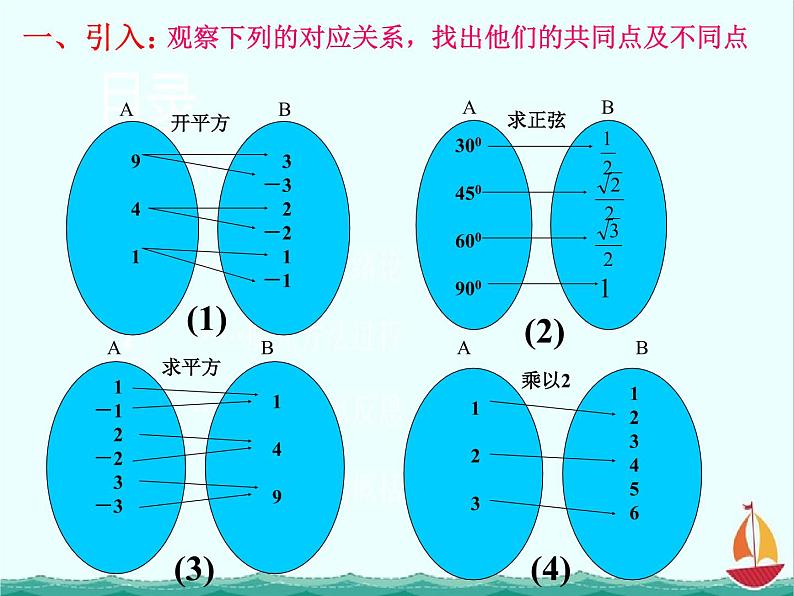
展开观察下列的对应关系,找出他们的共同点及不同点
(2)(3)(4)这三个对应的共同特点是: 对于左边集合A中的任何一个元素,按照某种对应法则f, 在右边集合B中 都有唯一的元素和它对应。
问题:怎样判断一个对应是不是映射?
解:根据映射定义,可以知道,(4)对应是A到B的映射。⑴、⑵、⑶对应不是A到B的映射。
例1:如下图所示的对应中,哪些是A到B的映射?
例2、 下列对应是不是A到B的映射?(1) A={1,2,3,4},B={3,4,5,6,7,8,9} f:乘2加1(2) A=N+,B={0,1} f: x 除以2得的余数(3) A=R+,B=R,f:求平方根(4) A={x|0≤ x<1},B={y|y≥1} f:取倒数
解(1) 是 (2) 是 (3)不是。B中有两个元素与A中一个元素对应 (4) 不是。A中元素0在B中无元素与之对应
已知(x,y)在映射f下的象是(2x,x+y),求:(1)(1,5)在f下的象;(2)(1,3)在f下的原象.
1、映射三要素:二个集合 (即象集、原象集)、 一 种对应关系,三者缺一不可
2、集合 A中的元素一定有象,且唯一;
3、集合 B中的元素不一定有原象,即使有也未必唯一;
5、 A到B 的映射与B 到A 的映射是两个不同的映射(方向不同,映射也不同)。
4、 A、B可以是数集,也可以是点集或其他集合;
判断这两个对应是否是映射?如果是,他们有什么特点?
有两个特点: ①集合A中不同的元素在B中有不同的象(意即不是多对一). ②集合B中的元素都有原象(没有多余的象) 这样的映射,比较特殊
定义:设A,B是两个集合,f是集合A到集合B的映射,如果在这个映射下,对于集合A中不同的元素在B中有不同的象,而且集合B中的每一个元素都有原象,这样的映射叫做A到B上的一一映射
注意:①一一映射中集合A中不同的元素在B中有不 同的象,集 合 B中的元素在A中都有原象②A={原象},B={象},若B≠{象}则这个映射就不是A到B上的一一映射
人教版新课标B选修1-22.1.1合情推理课文配套ppt课件: 这是一份人教版新课标B选修1-22.1.1合情推理课文配套ppt课件
高中数学人教版新课标B选修1-22.1.1合情推理图片ppt课件: 这是一份高中数学人教版新课标B选修1-22.1.1合情推理图片ppt课件,
人教版新课标B必修12.1.1函数图文课件ppt: 这是一份人教版新课标B必修12.1.1函数图文课件ppt,共28页。PPT课件主要包含了自学提纲,填写下图中对应关系,一对一,多对一,当x5时y3等内容,欢迎下载使用。













