高中数学沪教版高中一年级 第一学期2.1不等式的基本性质导学案

2.2 (3)一元二次不等式的解法

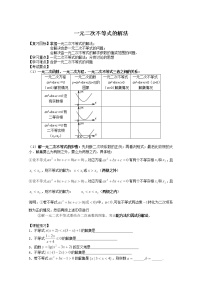
一、教学目标设计

   掌握用区间表示集合的方法；通过变式教学，学会用一元二次不等式解决几种类型的数学问题，体会数学知识之间的内在联系，形成逻辑思维能力；初步会用不等式解决一些简单的实际问题，增加数学学习的兴趣和用已学知识解决实际问题的意识。

二、教学重点及难点

   用区间表示不等式组的解集；会用不等式解决一些简单的实际问题。

三、教学流程设计

四、教学过程设计

一、 学习如何用区间来表示不等式的解集

1．              用区间来表示不等式的解集

设a，b都为实数，并且a<b,我们规定:

(1)             集合{x}叫做闭区间,表示为；

(2)             集合{x}叫做开区间,表示为；

(3)             集合{x}或{x}叫做半开半闭区间,分别表示

为, 。

  （4） 把实数集R表示为（-，+）；

        把集合{x}表示为[a，+；

        把集合{x}表示为(a,+)；

        把集合{x}表示为（-，b]；

        把集合{x}表示为（-，b）；

在上述所有的区间中，a，b叫做区间的端点，以后我们可以用区

间表示不等式的解集。

2．区间在数轴上的表示

[a，b]    （a，b）

[a，b）  （a，b]

[

[a，+） （a，+）

（-，b] （-，b）

   3．练习

   将上节课中不等式的解集用区间表示。

二、典型例题

例1．解不等式组：

3x-7x-100,      ①

  2x-5x+20        ②   

解：由不等式①的解集为,不等式②的解集为，可知原不等式组的解集为，它在数轴上的表示如图：

   [说明]：解由两个或两个以上的不等式组成的不等式组的解，可以将解集表示在同一条数轴上，这样更直观和清晰。能否在数轴上准确的找到几个解集的公共部分，对一部分学生解决这个问题有一定的困难。

   巩固练习：解下列不等式组：

      （1）  x-2x-3>0 ,           (2)   5-x>4x ,

             x+x-2>0 .                  3x-5x<0 .

   例2．(1)写出一个一元二次不等式,使它的解集为(-1,3).

   (2)若不等式ax+bx+3>0的解为-<x<3,求实数 a,b的值.

   解:(1)(x+1)(x-3)<0,即x-2x-3<0是一个解集为(-1,3)的一元二次不等式.

   (2)解法一:可得方程ax+bx+3=0的两个根为-,3,且a<0.所以运用根与系数的关系得：-=且=-,              即a=-2,b=5.

      解法二:方程(x+)(x-3)<0即x-x-<0的解为-<x<3,所以a=-2,b=5.

   [说明]：要让学生知道解集为(-1,3)的一元二次不等式有无数个,形如ax-2ax-3a<0(a0)或ax-2ax-3a0(a0)的不等式都满足条件,但二次项系数为1的不等式只有一个。

   拓展练习:若不等式ax+bx+c>0的解集为(-2,3),求不等式cx+ax-b<0的解集.

   例3.当k为何值时,关于x的一元二次不等式x+(k-1)x+4>0的解集为(-,+)?

   解:函数y= x+(k-1)x+4的图像是开口向上的抛物线.因为不等式x+(k-1)x+4>0的解集为(-,+),所以整条抛物线在x轴上方,此时方程x+(k-1)x+4=0的<0.解得k(-3,5).

   所以当-3<k<5时, 不等式x+(k-1)x+4>0的解集为(-,+).

   [说明]：等价于问题“当k为何值时，函数y=x+(k-1)x+4的图像全部在x轴的上方”。教师可以将例3改编成：“当k为何值时,关于x的一元二次不等式x+(k-1)x+4〈0的解集为空集?”进一步让学生理解一元二次不等式，一元二次方程和二次函数之间的关联。

   拓展练习：当k为何值时，不等式2kx+kx-0对于一切实数x都成立？

   例4.国家为了加强对烟酒生产的宏观管理，除了应用税收外，还征收附加税。已知某种酒每瓶销售价为70元，不收附加税时，每年大约产销100万瓶;若征收附加税,每销100元要征附加税r元(叫做税率r%),则每年的产销量将减少10r万瓶.如果要使每年在此项经营中所收取的附加税额不少于112万元,那么r              应怎样确定?

   解:设产销量为每年x(万瓶),则销售收入每年为70x(万元),从中征收附加税额为70xr%(万元),并且x=100-10r。

   由题意知 70(100-10r)r%112  即r-10r+160  解得 2r8。

   所以，税率定在2%至8%之间，年征收附加税额将不低于112万元。

[说明]由题意，应该用不等式解题，若用方程来列式则不能准确的表达题目的意思。需要注意不等式70(100-10r)r%112与方程70(100-10r)r%=112所表达的实际意义是不一样的。   巩固练习：距离码头南偏东60的400千米处有一个台风中心。已知台风以每小时40千米的速度向正北方向移动，距台风中心350千米以内都受台风影响。问从现在起多少小时后，码头将受台风影响，码头受台风影响的时间大约多久。

   三、课堂小结

   （1）我们可以借助数轴来求得不等式组的解集。

   （2）一些与一元二次不等式有关的问题，可以转化成相应的二次函数的问题，利用二次函数的图像，通过判断图像的开口，与x轴的交点情况来帮助解决问题。

（3）初步了解一元二次不等式在实际生活中的应用

四、作业布置

练习2.2(3),习题2.2

补充练习:

(1)已知集合A={x},集合B={x},求AB与AB.

(2)不等式<2的解集是R ,求实数k的取值范围.

(3)已知函数f(x)=x+px+q,且f(2)=2,若对于任意实数x恒有f(x)x,求实数p，q的值。

（4）某船从甲地沿河顺流航行75公里到达乙码头，停留30分钟后再逆流航行42公里到达丙地。假如水流每小时4公里。要在2小时内完成航行任务，则船速每小时至少需要多少公里？

七、教学设计说明

1．这是两节习题课，通过对几个典型例题的学习，让学生了解和

掌握一元二次不等式的简单应用，更进一步的了解不等式，方程和函数之间的关联，培养学生化归（不等式和函数的相互转化）和数形结合的数学思想，增加数学的应用意识。

   四个例题之间的联系不大，可单独处理。教学中设计了针对例题的巩固练习，拓展练习和补充练习，教师可以根据学生的实际水平和教学进度自行选取。

2．利用数轴求几个不等式解集的交集或并集，既直观又清晰。但是学生对于这种方法的使用还不熟练，在课堂教学中，教师要带动学生积极动手进行实践。

在应用题教学中，学生会习惯于用方程来解题。教师要帮助学生仔细阅读分析题意，讨论方程和不等式哪种形式更符合题意，体会一元二次不等式在实际生活中的应用。