高中数学2.1不等式的基本性质学案设计

2.2（1）一元二次不等式的解法

一、教学目标设计

掌握用二次函数的图像解一元二次不等式的解法。了解一元二次不等式、一元二次方程和二次函数之间的联系，体会数形结合、化归的数学思想。形成利用一般与特殊的关系来解决数学问题的能力。

二、教学重点及难点

   一元二次不等式的解法。利用二次函数的图像解一元二次不等式。

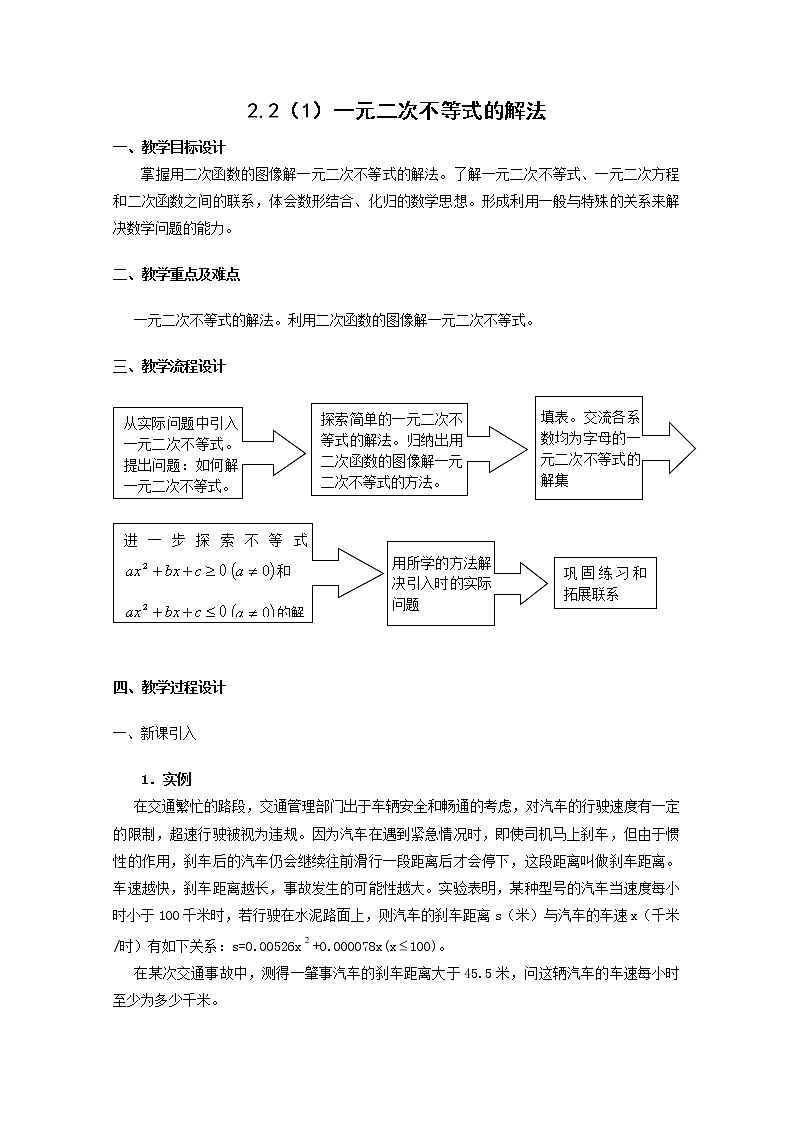
三、教学流程设计

四、教学过程设计

一、新课引入

1．实例

在交通繁忙的路段，交通管理部门出于车辆安全和畅通的考虑，对汽车的行驶速度有一定的限制，超速行驶被视为违规。因为汽车在遇到紧急情况时，即使司机马上刹车，但由于惯性的作用，刹车后的汽车仍会继续往前滑行一段距离后才会停下，这段距离叫做刹车距离。车速越快，刹车距离越长，事故发生的可能性越大。实验表明，某种型号的汽车当速度每小时小于100千米时，若行驶在水泥路面上，则汽车的刹车距离s（米）与汽车的车速x（千米/时）有如下关系：s=0.00526x+0.000078x(x100)。

在某次交通事故中，测得一肇事汽车的刹车距离大于45.5米，问这辆汽车的车速每小时至少为多少千米。

根据题意，得0.00526x+0.000078x45.5。------①

   2．提出问题

   ①是一个整式不等式，它只含有一个未知数，并且未知数的最高次数是二次，这样的不等式叫做一元二次不等式。

一元二次不等式的一般形式是：

如何解一元二次不等式？

   [说明]由教材（P）中的实例引出本节课的学习内容。

二、解法探究

为了得到一元二次不等式的一般解法，不妨先研究一个简单的

一元二次不等式 的解法。

解法一：原不等式可化为 ，它等价与

将问题转化为我们学过的一元一次不等式组。于是可得到原不等式的解集

     解法二、利用数轴 ， －1、3将数轴分成三个部分，

当时，  所以

    当时，  所以

    当时，  所以

可得原不等式的解集    

还可得到解集为。

   解法三、利用二次函数图像求此不等式的的解集也可看作求二次函数取正值时的取值范围，即求该二次函数的图像

在轴上方时的取值范围。

我们知道，二次函数 的图像是一条开口向上的抛物线，它与轴有两个交点，由方程的解可得交点的横坐标分别是 ， ，容易看出，当时上述函数的图像在轴上方， ；当时，上述函数的图像在轴下方，即 ，于是可得不等式解集为。

   [说明]解法一中解两个一元一次不等式组中涉及的“或”和“且”的关系可用集合中的交集和并集来说明。解法三利用二次函数的图象更加直观，清晰，是高中阶段解一元二次不等式的主要方法。

例1．利用二次函数图像解下列不等式。

    （1）            （2）

[说明]点评中强调一元二次方程，一元二次不等式和二次函数之间的联系。由学生归纳如何利用二次函数的图像解二次项系数为正的一元二次不等式的主要步骤：求出相应的一元二次方程的解；画出相应的二次函数的图像；写出不等式的解集。第2小题函数的图像与x轴相切，教师可提示学生思考如果图像与x轴相离时的不等式的解的情况。

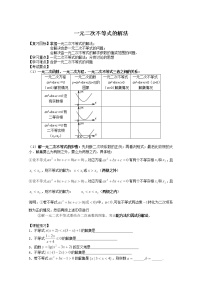
例2．填表：

提问：如何解二次项系数为负的一元二次不等式？

[说明]特别注意和时不等式的解集。二次项系数为负的一元二次不等式可通过转化为二次项系数为正的一元二次不等式或者直接用开口向下二次函数的图像来解。特别注意不等式的解集为空集或全集时的条件。

提问：对照表格，如何解不等式和

？

三、解决新课引入时的实际问题

利用上面介绍的一元二次不等式的解法，可得①式的解为x>93.00或x<-93.01.

根据题意，可推断这辆汽车在发生交通事故时的车速应大于93千米/时。这条信息将成为车祸责任认定的重要依据。

四、课堂练习

解下列不等式：

（1）2x-3x-20         （2）-3x+x+1>0

(3)9x+6x+1>0             (4)4x-x<5

(5)2x+x+10

五、作业布置

练习2.2(1)；练习2.2(2)

七、教学设计说明

  1．本节课开始引入时利用课本例子，因为教材的例子是难得的实例，充分利用教材，让学生阅读，也可节省时间，直截了当明确本节课的任务。数学教学的本质是思维活动的过程，如何解决提出的问题？将一般问题特殊化，特例起到抛砖引玉的作用，再由特殊回到一般，这是数学中处理问题的常用方法。

  2．在解的时候，解法一是运用了化归的数学思想，把一个生疏、复杂的问题转化为熟悉、简单的问题来处理。化归的思想贯穿了解不等式这一章，分式不等式转化为整式不等式，含绝对值的不等式转化为不含绝对值的不等式，无理不等式转化为有理不等式，超越不等式转化为代数不等式，高次不等式转化为低次不等式。

  3．本堂课采用让学生自主探究的学习方式，在教师的引导下，通过对几个具有代表性的简单的一元二次不等式的求解归纳出一元二次不等式的解法。对于程度较好的学生，教师可隐去例2表格中的第一和第二行。利用二次函数的图像不仅解决了求一元二次不等式解的问题，而且还能求解形如，的不等式。函数、方程、不等式之间的联系是中学数学极其重要，也是非常精彩的内容，教师要不失时机的渗透，引导学生体会其中的奥妙。