








所属成套资源:人教版初中数学七年级下册全册课件+教案+练习
初中数学人教版七年级下册8.2 消元---解二元一次方程组优秀课件ppt
展开这是一份初中数学人教版七年级下册8.2 消元---解二元一次方程组优秀课件ppt,文件包含人教版七年级下册82消元解二元一次方程组课件ppt、人教版七年级下册82消元解二元一次方程组同步练习doc、人教版七年级下册82消元解二元一次方程组教学设计doc等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
问题:设大马车装了x个包裹 , 小马车装了y个包裹。大马车的包裹数比小马车的多2个,由此你能得到怎样的方程呢?
大马车包裹数-小马车的包裹数=2个
若大马车从小马车中拿来1个包裹,这时大马车包裹数是小马车的2倍,它们各有几个包裹?由此你又能得到怎样的方程呢?
大马车包裹数+1=2×(小马车包裹数-1)
回顾:上节课我们学习了二元一次方程(组)及它们解的含义。本节课我们将一起学习二元一次方程(组)的解法。
问题:1.这个二元一次方程组有解吗? 2.如何来解呢?
有无数组解,只要是满足方程的一组x和y都可以。
1.发现:一般一个二元一次方程无法求出它的解,有无数组解。
2.问题:如果给 一个特殊条件,如x和y是不大于4的正整数,你可以求出满足条件的所有解码?
满足限定条件,可以根据题意求出符合的解
1.求二元一次方程3x+2y=19的正整数解。
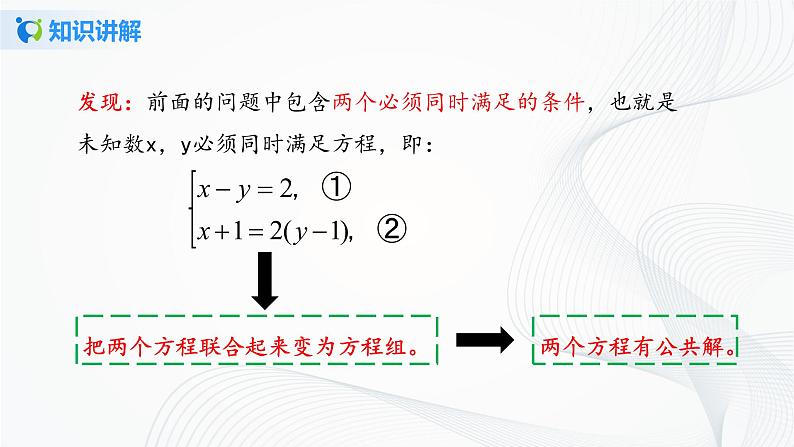
发现:前面的问题中包含两个必须同时满足的条件,也就是未知数x,y必须同时满足方程,即:
把两个方程联合起来变为方程组。
解析:将x=y+2代入②,得: y+2+1=2(y-1) 解得:y=5 将y=5代入x=y+2, x=7
二元一次方程组的解法:①代入消元法
思考:如果把①改写为“x=y+2 或者y=x-2 ”,同②再组合,你能解除x或者y吗?
转化为一元一次方程,得解。
2.用代入法解方程组。
解:由②,得y=2x+5 ③ 把③代入①,得 4x+3(2x+5)=5 整理得:x= -1 将x=代入③得:y=3 所以原方程组的解是
①将其中一个未知数用另一个未知数表示出来;②将变形的方程代入另一个方程,转化为一元一次方程;③整理方程,解得其中一个未知数;④将已解的结果代入前面已知方程求另一个未知数即可。
归纳1:代入法解二元一次方程组的步骤:
代入法求二元一次方程技巧
1.方程组中有一个未知数的系数为1或者-1;2.方程组中两个方程相同未知数的系数相等或者倍数关系。
1.含有系数是1或-1的方程:
2.如果有系数是倍数关系:
二元一次方程组的解法:②加减消元法
思考:如果用代入消元法求解方程组可以吗?
解析:由①-②,得:9y=-18 解得:y=-2 将y=-2代入①, 得x=5
分析:我们还可以将①-②进行消元,消去x
整理,可以求出方程组的解。
解:①×2,得 8x+10y=46 ③ ②×5,得25x-10y=20 ④由③+④,得33x=66 ,∴ x=2把x=2代入②,得5×2-2y=4,y=3所以这个方程组的解是
3.用加减法解二元一次方程组。
①变形:系数相同或者相反时,进行相减或者相加;②消元:转化为一元一次方程;③求解:整理方程,解得其中一个未知数;④将已解的结果代入前面已知方程求另一个未知数即可。
归纳2:加(减)法解二元一次方程组的步骤:
加减法求二元一次方程技巧
当方程组中同一未知数的系数的绝对值不相等时,必须用等式性质来改变方程组中方程的形式,得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件。
1.二元一次方程解的情况?
3.二元一次方程组解法代入和加减消元的步骤?
1.选择适当的消元方法解二元一次方程组
2.选择适合的方法解二元一次方程组
1.写用代入法解方程组:
2.已知方程组 的解满足x+y=3,则k的值为 。
课后练习:1. ;2. 8
相关课件
这是一份人教版七年级下册8.2 消元---解二元一次方程组获奖ppt课件,共25页。PPT课件主要包含了温故知新,①变形,②加减,③求解,④回代,⑤写解,素养目标,课堂导入,新知探究,等量关系等内容,欢迎下载使用。
这是一份初中数学人教版七年级下册8.2 消元---解二元一次方程组获奖ppt课件,共25页。
这是一份初中数学人教版七年级下册8.2 消元---解二元一次方程组示范课课件ppt,共37页。PPT课件主要包含了逐点导讲练,课堂小结,作业提升,学习目标,课时讲解,课时流程,知识点,感悟新知,代入消元法等内容,欢迎下载使用。














