人教版新课标B选修2-13.2 空间向量在立体几何中的应用教案配套ppt课件

这是一份人教版新课标B选修2-13.2 空间向量在立体几何中的应用教案配套ppt课件，共13页。PPT课件主要包含了求异面直线的距离，练习如图，求点到平面的距离，结论1等内容，欢迎下载使用。
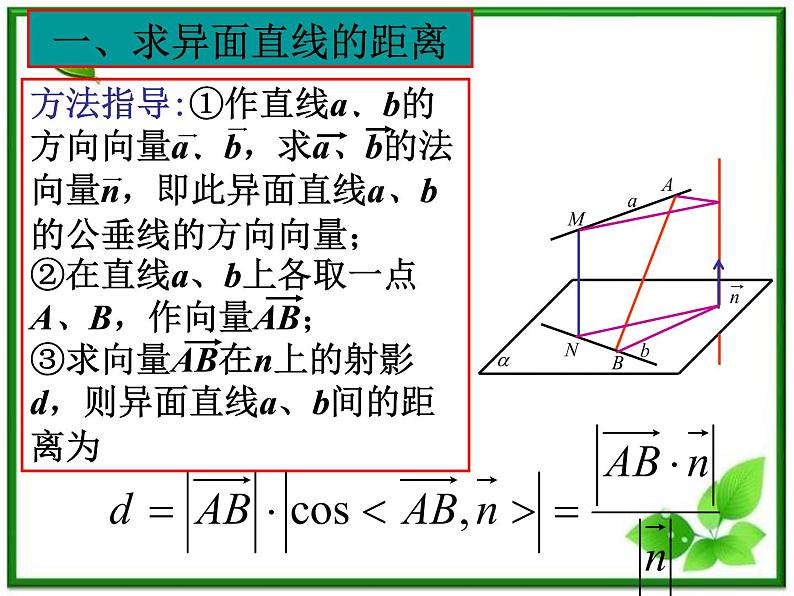
方法指导:①作直线a、b的 方向向量a、b，求a、b的法 向量n，即此异面直线a、b 的公垂线的方向向量； ②在直线a、b上各取一点 A、B，作向量AB； ③求向量AB在n上的射影 d，则异面直线a、b间的距离为
例2：已知正方体ABCD-A1B1C1D1的棱长为1，求异面直线DA1与AC的距离。
例3、已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2,E、F分别是AB、AD的中点，求点B到平面GEF的距离。
如图点P为平面外一点，点A为平面内的任一点，平面的法向量为n,过点P作平面的垂线PO，记PA和平面所成的角为，则点P到平面的距离
例4、已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2,E、F分别是AB、AD的中点，求直线BD到平面GEF的距离。
三、求直线与平面间距离
例5、在边长为1的正方体ABCD-A1B1C1D1中，M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点，求平面AMN与平面EFDB的距离。
四、求平行平面与平面间距离
1、怎样利用向量求距离？
点到平面的距离：连结该点与平面上任意一点的向量在平面定向法向量上的射影（如果不知道判断方向，可取其射影的绝对值）。
点到直线的距离：求出垂线段的向量的模。
直线到平面的距离：可以转化为点到平面的距离。
平行平面间的距离：转化为直线到平面的距离、点到平面的距离。
异面直线间的距离：转化为直线到平面的距离、点到平面的距离。也可运用闭合曲线求公垂线向量的模或共线向量定理和公垂线段定义求出公垂线段向量的模。