人教版新课标A选修2-21.1变化率与导数教课ppt课件

这是一份人教版新课标A选修2-21.1变化率与导数教课ppt课件，共18页。PPT课件主要包含了①平均变化率，②割线的斜率，关键是求出，导数的几何意义，函数导函数，看一个例子，下面把前面知识小结等内容，欢迎下载使用。
了解函数的平均变化率 教学重点：函数的平均变化率
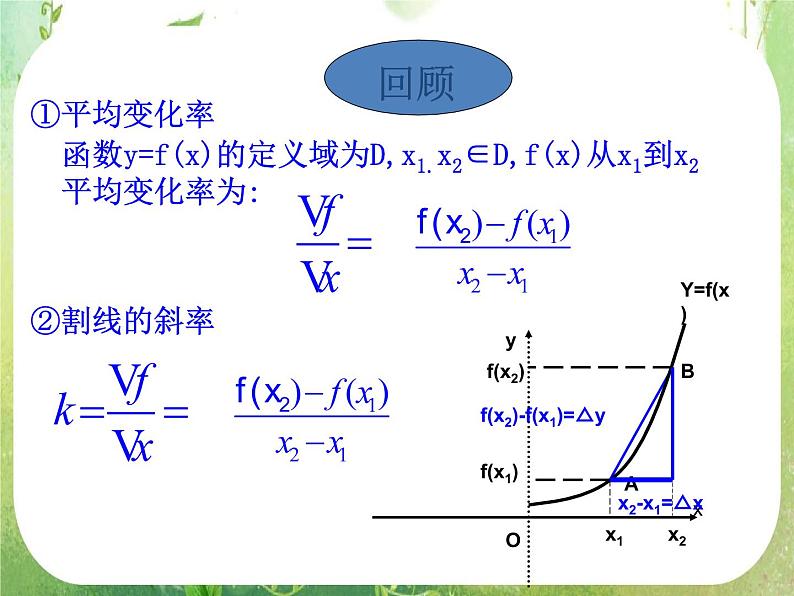
函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:
以平均速度代替瞬时速度，然后通过取极限，
从瞬时速度的近似值过渡到瞬时速度的精确值。
我们把物体在某一时刻的速度称为瞬时速度.
从函数y=f(x)在x=x0处的瞬时变化率是:
我们称它为函数y=f(x)
在x=x0处的导数，记作f′ (x0)或y′|x→x0即
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
注意:这里的增量不是一般意义上的增量,它可正也可负. 自变量的增量Δx的形式是多样的,但不论Δx选择 哪种形式, Δy也必须选择与之相对应的形式.
例1 将原油精练为汽油、柴油、塑胶等各种不同产品，需要对原油进行冷却和加热。如果第 x(h)时，原油的温度（单位：0C）为 f(x)=x2-7x+15(0≤x≤8).计算第2（h) 和第6（h）时，原由温度的瞬时变化率，并说明它们的意义。
它说明在第2（h)附近，原油温度大约以3 0C/h的速度下降；在第6（h)附近，原油温度大约以5 0C/H的速度上升。
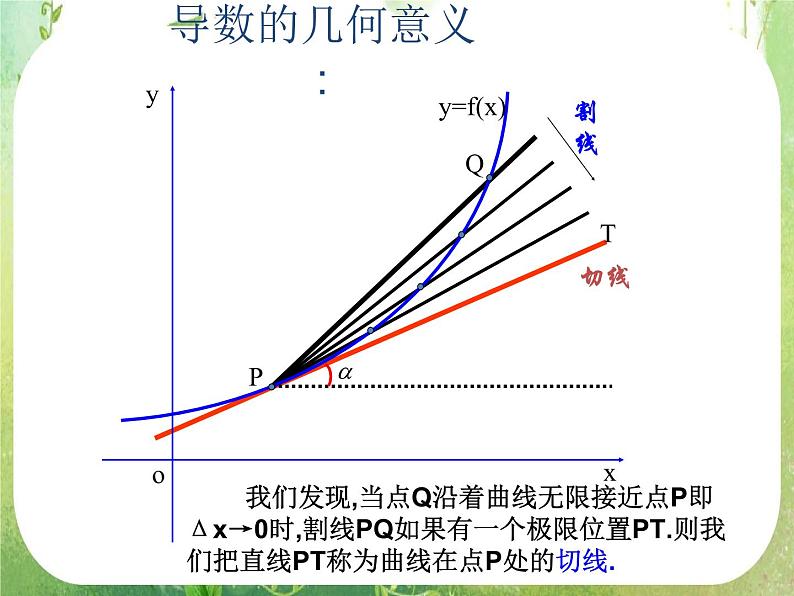
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
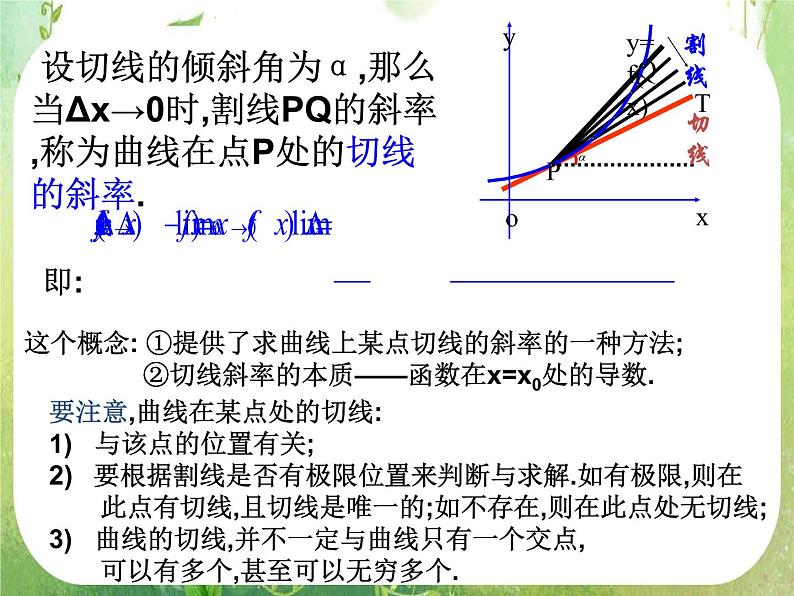
设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
这个概念: ①提供了求曲线上某点切线的斜率的一种方法; ②切线斜率的本质——函数在x=x0处的导数.
要注意,曲线在某点处的切线: 1) 与该点的位置有关; 要根据割线是否有极限位置来判断与求解.如有极限,则在 此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3) 曲线的切线,并不一定与曲线只有一个交点, 可以有多个,甚至可以无穷多个.
因此,切线方程为y-2=2(x-1),即y=2x.
求曲线在某点处的切线方程的基本步骤:①求出P点的坐标;②利用切线斜率的定义求 出切线的斜率;③利用点斜式求切线方程.
即点P处的切线的斜率等于4.
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
在不致发生混淆时，导函数也简称导数．
由函数f(x)在x=x0处求导数的过程可以看到,当时,f’(x0) 是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:
如何求函数y=f(x)的导数?
a.导数是从众多实际问题中抽象出来的具有相同的数 学表达式的一个重要概念，要从它的几何意义和物 理意义认识这一概念的实质，学会用事物在全过 程中的发展变化规律来确定它在某一时刻的状态。
b.要切实掌握求导数的三个步骤：（1）求函数的增 量；（2）求平均变化率；（3）取极限，得导数。
（1）函数在一点处的导数，就是在该点的函数的改 变量与自变量的改变量之比的极限，它是一个 常数，不是变数。
c.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数” 之间的区别与联系。
无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想，丢掉极限思想就无法理解导 数概念。