2020-2021学年2.4 平面向量的数量积授课ppt课件

这是一份2020-2021学年2.4 平面向量的数量积授课ppt课件，共17页。PPT课件主要包含了例题讲解，小结回顾，新课讲解，性质讲解，课堂练习，θ180°，θ90°，向量的夹角，θ0°，特殊情况等内容，欢迎下载使用。
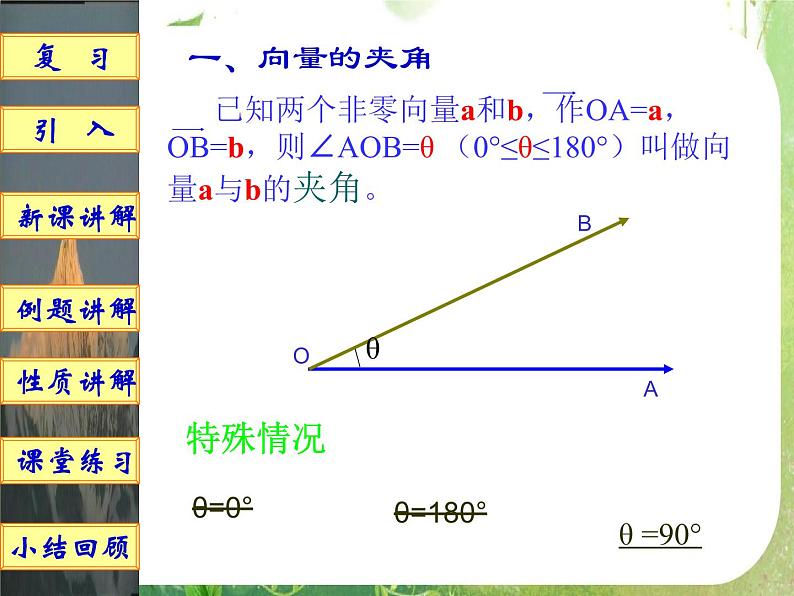
已知两个非零向量a和b，作OA=a， OB=b，则∠AOB=θ （0°≤θ≤180°）叫做向量a与b的夹角。
二、向量数量积的定义 已知两个非零向量a与b，它们的夹角为θ，我们把数量|a| |b|csθ叫做a与b的数量积（或内积），记作a·b a·b=|a| |b| csθ
规定:零向量与任一向量的数量积为0。说明:1、符号”·”在向量运算中不是乘 号,既不省略,也不能用”×”代替. 2、数量积是实数而不是向量
我们得到a·b的几何意义：数量积a·b等于a的模长|a|与b在a的方向上的投影|b|csθ的乘积。
三、向量数量积的几何意义
设a，b都是非零向量，e是与b方向相同的单位向量，θ是a与e的夹角，则 （1）e·a=a·e = |a| csθ
（5）|a·b|≤|a||b|
（1） a·b=b·a（交换律）
（2）（ a）·b= （a·b）＝a·（ b）（数乘结合律）
（3）（a+b) ·c=a·c+b·c（分配律）
注：许多运算律与实数不同 如(a·b) ·c=a·(b·c)不成立 又如a·b=b·c则a=c亦不成立
4. 运算律
当θ=0°时，a与b同向
当θ=180°时，a与b反向。
θ =90°，a与b垂直，记作a⊥b。
当θ=0°时，它是|b|
当θ=180°时，它是－|b|。
当θ=90°，它是0。
当θ为锐角时，它是正值；
当θ为钝角时，它是负值；
解：a·b=|a| |b|csθ=5×4×cs120° =5×4×（-1/2）= －10。
例1 已知|a|=5，|b|=4，a与b的夹角θ=120°，求a·b。
例2 已知a=(1,1),b=(2,0),求a·b。
解： |a| =√2, |b|=2, θ=45 °∴ a·b=|a| |b|csθ= √2×2×cs45 ° = 2